Dictionary Learning and Sparse Coding on Statistical Manifolds
Paper and Code
May 03, 2018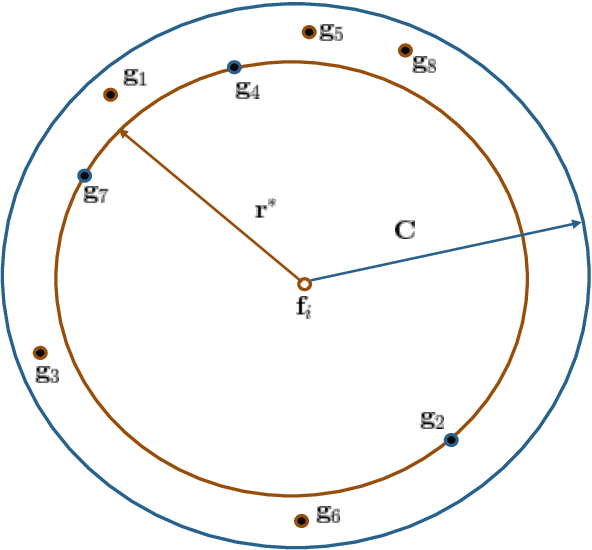



In this paper, we propose a novel information theoretic framework for dictionary learning (DL) and sparse coding (SC) on a statistical manifold (the manifold of probability distributions). Unlike the traditional DL and SC framework, our new formulation does not explicitly incorporate any sparsity inducing norm in the cost function being optimized but yet yields sparse codes. Our algorithm approximates the data points on the statistical manifold (which are probability distributions) by the weighted Kullback-Leibeler center/mean (KL-center) of the dictionary atoms. The KL-center is defined as the minimizer of the maximum KL-divergence between itself and members of the set whose center is being sought. Further, we prove that the weighted KL-center is a sparse combination of the dictionary atoms. This result also holds for the case when the KL-divergence is replaced by the well known Hellinger distance. From an applications perspective, we present an extension of the aforementioned framework to the manifold of symmetric positive definite matrices (which can be identified with the manifold of zero mean gaussian distributions), $\mathcal{P}_n$. We present experiments involving a variety of dictionary-based reconstruction and classification problems in Computer Vision. Performance of the proposed algorithm is demonstrated by comparing it to several state-of-the-art methods in terms of reconstruction and classification accuracy as well as sparsity of the chosen representation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge