VolterraNet: A higher order convolutional network with group equivariance for homogeneous manifolds
Paper and Code
Jun 05, 2021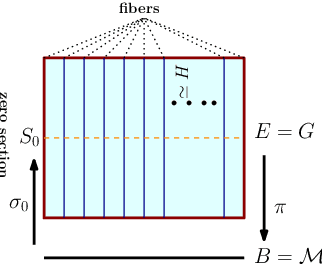
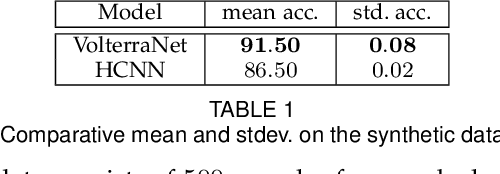


Convolutional neural networks have been highly successful in image-based learning tasks due to their translation equivariance property. Recent work has generalized the traditional convolutional layer of a convolutional neural network to non-Euclidean spaces and shown group equivariance of the generalized convolution operation. In this paper, we present a novel higher order Volterra convolutional neural network (VolterraNet) for data defined as samples of functions on Riemannian homogeneous spaces. Analagous to the result for traditional convolutions, we prove that the Volterra functional convolutions are equivariant to the action of the isometry group admitted by the Riemannian homogeneous spaces, and under some restrictions, any non-linear equivariant function can be expressed as our homogeneous space Volterra convolution, generalizing the non-linear shift equivariant characterization of Volterra expansions in Euclidean space. We also prove that second order functional convolution operations can be represented as cascaded convolutions which leads to an efficient implementation. Beyond this, we also propose a dilated VolterraNet model. These advances lead to large parameter reductions relative to baseline non-Euclidean CNNs. To demonstrate the efficacy of the VolterraNet performance, we present several real data experiments involving classification tasks on spherical-MNIST, atomic energy, Shrec17 data sets, and group testing on diffusion MRI data. Performance comparisons to the state-of-the-art are also presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge