Victoria Crawford
An information theoretic formulation of the Dictionary Learning and Sparse Coding Problems on Statistical Manifolds
Feb 03, 2017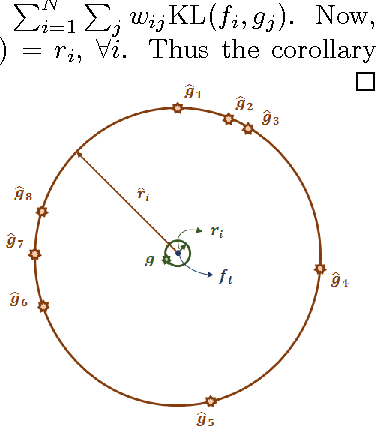
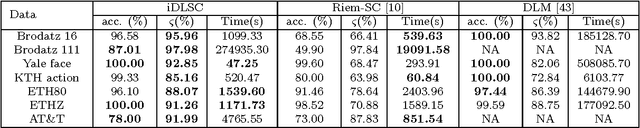
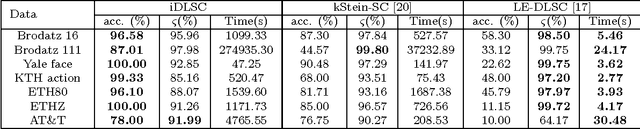
Abstract:In this work, we propose a novel information theoretic framework for dictionary learning (DL) and sparse coding (SC) on a statistical manifold (the manifold of probability distributions). Unlike the traditional DL and SC framework, our new formulation {\it does not explicitly incorporate any sparsity inducing norm in the cost function but yet yields SCs}. Moreover, we extend this framework to the manifold of symmetric positive definite matrices, $\mathcal{P}_n$. Our algorithm approximates the data points, which are probability distributions, by the weighted Kullback-Leibeler center (KL-center) of the dictionary atoms. The KL-center is the minimizer of the maximum KL-divergence between the unknown center and members of the set whose center is being sought. Further, {\it we proved that this KL-center is a sparse combination of the dictionary atoms}. Since, the data reside on a statistical manifold, the data fidelity term can not be as simple as in the case of the vector-space data. We therefore employ the geodesic distance between the data and a sparse approximation of the data element. This cost function is minimized using an acceleterated gradient descent algorithm. An extensive set of experimental results show the effectiveness of our proposed framework. We present several experiments involving a variety of classification problems in Computer Vision applications. Further, we demonstrate the performance of our algorithm by comparing it to several state-of-the-art methods both in terms of classification accuracy and sparsity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge