A CNN for homogneous Riemannian manifolds with applications to Neuroimaging
Paper and Code
Aug 06, 2018
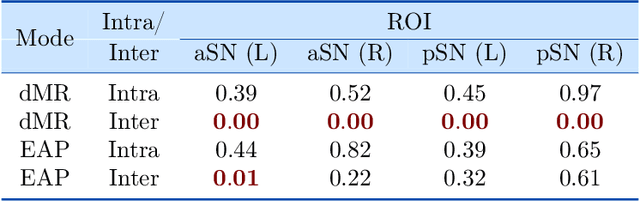
Convolutional neural networks are ubiquitous in Machine Learning applications for solving a variety of problems. They however can not be used in their native form when the domain of the data is commonly encountered manifolds such as the sphere, the special orthogonal group, the Grassmanian, the manifold of symmetric positive definite matrices and others. Most recently, generalization of CNNs to data domains such as the 2-sphere has been reported by some research groups, which is referred to as the spherical CNNs (SCNNs). The key property of SCNNs distinct from CNNs is that they exhibit the rotational equivariance property that allows for sharing learned weights within a layer. In this paper, we theoretically generalize the CNNs to Riemannian homogeneous manifolds, that include but are not limited to the aforementioned example manifolds. Our key contributions in this work are: (i) A theorem stating that linear group equivariance systems are fully characterized by correlation of functions on the domain manifold and vice-versa. This is fundamental to the characterization of all linear group equivariant systems and parallels the widely used result in linear system theory for vector spaces. (ii) As a corrolary, we prove the equivariance of the correlation operation to group actions admitted by the input domains which are Riemannian homogeneous manifolds. (iii) We present the first end-to-end deep network architecture for classification of diffusion magnetic resonance image (dMRI) scans acquired from a cohort of 44 Parkinson Disease patients and 50 control/normal subjects. (iv) A proof of concept experiment involving synthetic data generated on the manifold of symmetric positive definite matrices is presented to demonstrate the applicability of our network to other types of domains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge