ManifoldNet: A Deep Network Framework for Manifold-valued Data
Paper and Code
Sep 20, 2018
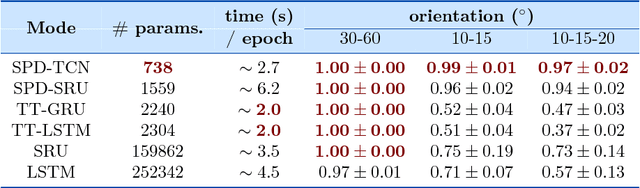

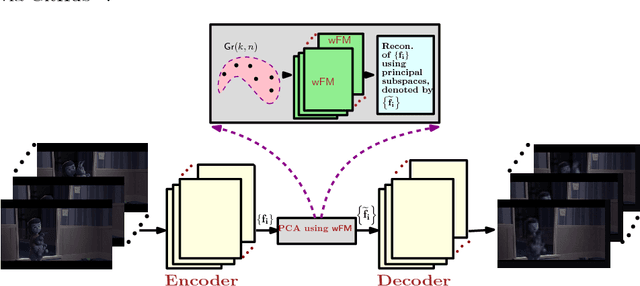
Deep neural networks have become the main work horse for many tasks involving learning from data in a variety of applications in Science and Engineering. Traditionally, the input to these networks lie in a vector space and the operations employed within the network are well defined on vector-spaces. In the recent past, due to technological advances in sensing, it has become possible to acquire manifold-valued data sets either directly or indirectly. Examples include but are not limited to data from omnidirectional cameras on automobiles, drones etc., synthetic aperture radar imaging, diffusion magnetic resonance imaging, elastography and conductance imaging in the Medical Imaging domain and others. Thus, there is need to generalize the deep neural networks to cope with input data that reside on curved manifolds where vector space operations are not naturally admissible. In this paper, we present a novel theoretical framework to generalize the widely popular convolutional neural networks (CNNs) to high dimensional manifold-valued data inputs. We call these networks, ManifoldNets. In ManifoldNets, convolution operation on data residing on Riemannian manifolds is achieved via a provably convergent recursive computation of the weighted Fr\'{e}chet Mean (wFM) of the given data, where the weights makeup the convolution mask, to be learned. Further, we prove that the proposed wFM layer achieves a contraction mapping and hence ManifoldNet does not need the non-linear ReLU unit used in standard CNNs. We present experiments, using the ManifoldNet framework, to achieve dimensionality reduction by computing the principal linear subspaces that naturally reside on a Grassmannian. The experimental results demonstrate the efficacy of ManifoldNets in the context of classification and reconstruction accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge