Towards Efficient Large Scale Spatial-Temporal Time Series Forecasting via Improved Inverted Transformers

Time series forecasting at scale presents significant challenges for modern prediction systems, particularly when dealing with large sets of synchronized series, such as in a global payment network. In such systems, three key challenges must be overcome for accurate and scalable predictions: 1) emergence of new entities, 2) disappearance of existing entities, and 3) the large number of entities present in the data. The recently proposed Inverted Transformer (iTransformer) architecture has shown promising results by effectively handling variable entities. However, its practical application in large-scale settings is limited by quadratic time and space complexity ($O(N^2)$) with respect to the number of entities $N$. In this paper, we introduce EiFormer, an improved inverted transformer architecture that maintains the adaptive capabilities of iTransformer while reducing computational complexity to linear scale ($O(N)$). Our key innovation lies in restructuring the attention mechanism to eliminate redundant computations without sacrificing model expressiveness. Additionally, we incorporate a random projection mechanism that not only enhances efficiency but also improves prediction accuracy through better feature representation. Extensive experiments on the public LargeST benchmark dataset and a proprietary large-scale time series dataset demonstrate that EiFormer significantly outperforms existing methods in both computational efficiency and forecasting accuracy. Our approach enables practical deployment of transformer-based forecasting in industrial applications where handling time series at scale is essential.

A Compact Model for Large-Scale Time Series Forecasting

Spatio-temporal data, which commonly arise in real-world applications such as traffic monitoring, financial transactions, and ride-share demands, represent a special category of multivariate time series. They exhibit two distinct characteristics: high dimensionality and commensurability across spatial locations. These attributes call for computationally efficient modeling approaches and facilitate the use of univariate forecasting models in a channel-independent fashion. SparseTSF, a recently introduced competitive univariate forecasting model, harnesses periodicity to achieve compactness by concentrating on cross-period dynamics, thereby extending the Pareto frontier with respect to model size and predictive performance. Nonetheless, it underperforms on spatio-temporal data due to an inadequate capture of intra-period temporal dependencies. To address this shortcoming, we propose UltraSTF, which integrates a cross-period forecasting module with an ultra-compact shape bank component. Our model effectively detects recurring patterns in time series through the attention mechanism of the shape bank component, thereby strengthening its ability to learn intra-period dynamics. UltraSTF achieves state-of-the-art performance on the LargeST benchmark while employing fewer than 0.2% of the parameters required by the second-best approaches, thus further extending the Pareto frontier of existing methods.

Discrete-state Continuous-time Diffusion for Graph Generation

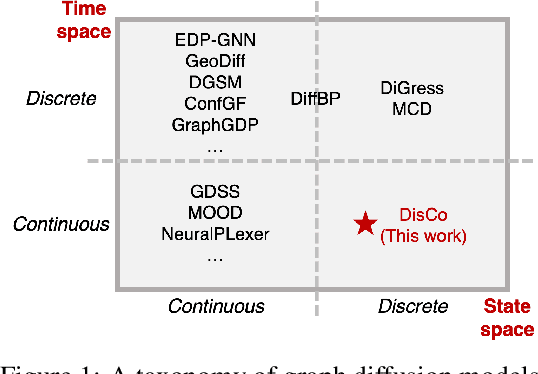
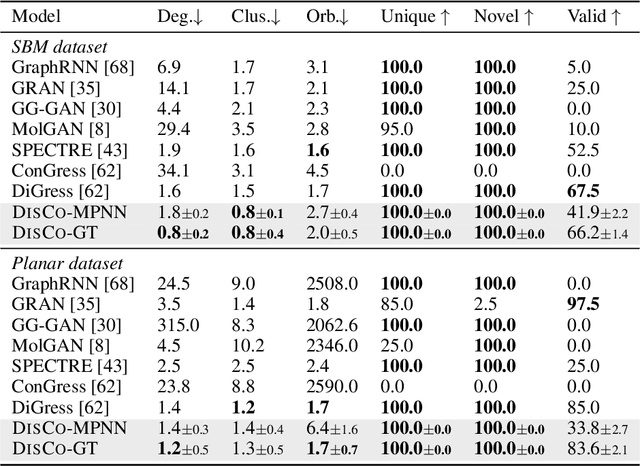
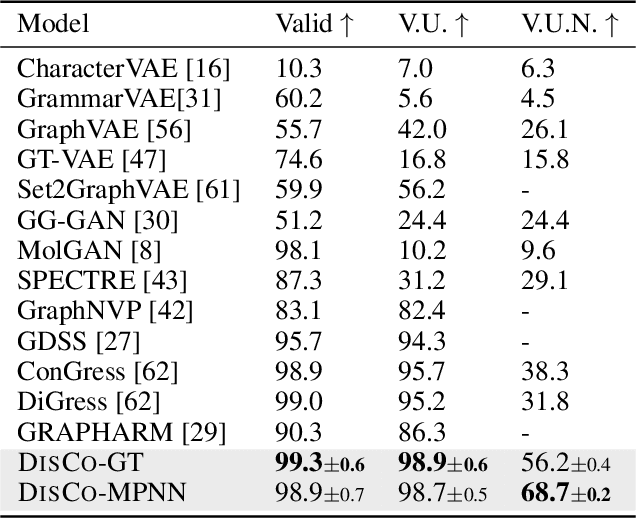
Graph is a prevalent discrete data structure, whose generation has wide applications such as drug discovery and circuit design. Diffusion generative models, as an emerging research focus, have been applied to graph generation tasks. Overall, according to the space of states and time steps, diffusion generative models can be categorized into discrete-/continuous-state discrete-/continuous-time fashions. In this paper, we formulate the graph diffusion generation in a discrete-state continuous-time setting, which has never been studied in previous graph diffusion models. The rationale of such a formulation is to preserve the discrete nature of graph-structured data and meanwhile provide flexible sampling trade-offs between sample quality and efficiency. Analysis shows that our training objective is closely related to generation quality, and our proposed generation framework enjoys ideal invariant/equivariant properties concerning the permutation of node ordering. Our proposed model shows competitive empirical performance against state-of-the-art graph generation solutions on various benchmarks and, at the same time, can flexibly trade off the generation quality and efficiency in the sampling phase.

Horocycle Decision Boundaries for Large Margin Classification in Hyperbolic Space

Hyperbolic spaces have been quite popular in the recent past for representing hierarchically organized data. Further, several classification algorithms for data in these spaces have been proposed in the literature. These algorithms mainly use either hyperplanes or geodesics for decision boundaries in a large margin classifiers setting leading to a non-convex optimization problem. In this paper, we propose a novel large margin classifier based on horocycle (horosphere) decision boundaries that leads to a geodesically convex optimization problem that can be optimized using any Riemannian gradient descent technique guaranteeing a globally optimal solution. We present several experiments depicting the performance of our classifier.

Nested Hyperbolic Spaces for Dimensionality Reduction and Hyperbolic NN Design

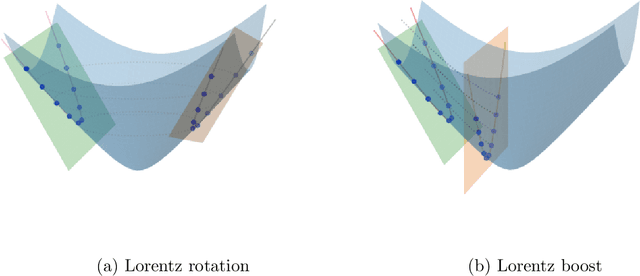
Hyperbolic neural networks have been popular in the recent past due to their ability to represent hierarchical data sets effectively and efficiently. The challenge in developing these networks lies in the nonlinearity of the embedding space namely, the Hyperbolic space. Hyperbolic space is a homogeneous Riemannian manifold of the Lorentz group. Most existing methods (with some exceptions) use local linearization to define a variety of operations paralleling those used in traditional deep neural networks in Euclidean spaces. In this paper, we present a novel fully hyperbolic neural network which uses the concept of projections (embeddings) followed by an intrinsic aggregation and a nonlinearity all within the hyperbolic space. The novelty here lies in the projection which is designed to project data on to a lower-dimensional embedded hyperbolic space and hence leads to a nested hyperbolic space representation independently useful for dimensionality reduction. The main theoretical contribution is that the proposed embedding is proved to be isometric and equivariant under the Lorentz transformations. This projection is computationally efficient since it can be expressed by simple linear operations, and, due to the aforementioned equivariance property, it allows for weight sharing. The nested hyperbolic space representation is the core component of our network and therefore, we first compare this ensuing nested hyperbolic space representation with other dimensionality reduction methods such as tangent PCA, principal geodesic analysis (PGA) and HoroPCA. Based on this equivariant embedding, we develop a novel fully hyperbolic graph convolutional neural network architecture to learn the parameters of the projection. Finally, we present experiments demonstrating comparative performance of our network on several publicly available data sets.