Discrete-state Continuous-time Diffusion for Graph Generation
Paper and Code
May 19, 2024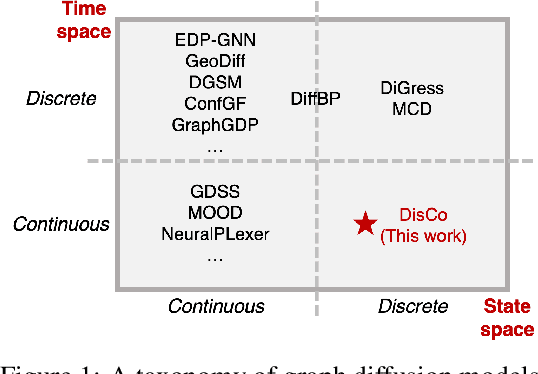
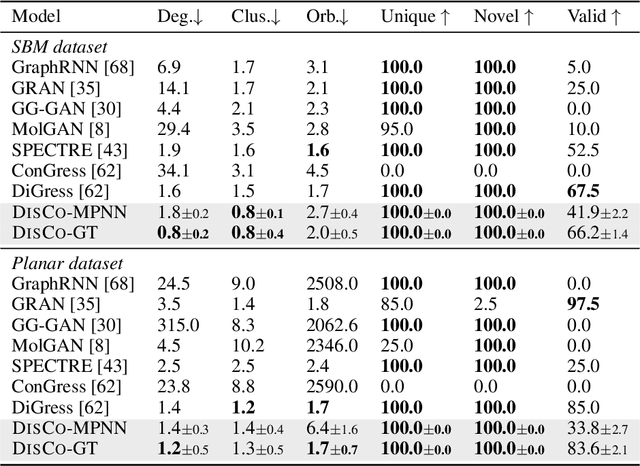

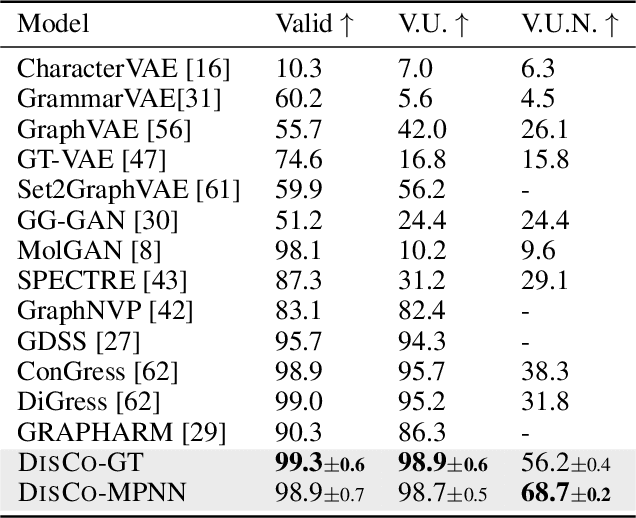
Graph is a prevalent discrete data structure, whose generation has wide applications such as drug discovery and circuit design. Diffusion generative models, as an emerging research focus, have been applied to graph generation tasks. Overall, according to the space of states and time steps, diffusion generative models can be categorized into discrete-/continuous-state discrete-/continuous-time fashions. In this paper, we formulate the graph diffusion generation in a discrete-state continuous-time setting, which has never been studied in previous graph diffusion models. The rationale of such a formulation is to preserve the discrete nature of graph-structured data and meanwhile provide flexible sampling trade-offs between sample quality and efficiency. Analysis shows that our training objective is closely related to generation quality, and our proposed generation framework enjoys ideal invariant/equivariant properties concerning the permutation of node ordering. Our proposed model shows competitive empirical performance against state-of-the-art graph generation solutions on various benchmarks and, at the same time, can flexibly trade off the generation quality and efficiency in the sampling phase.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge