GitEvolve: Predicting the Evolution of GitHub Repositories

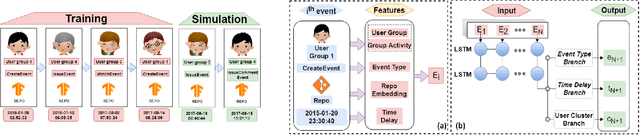
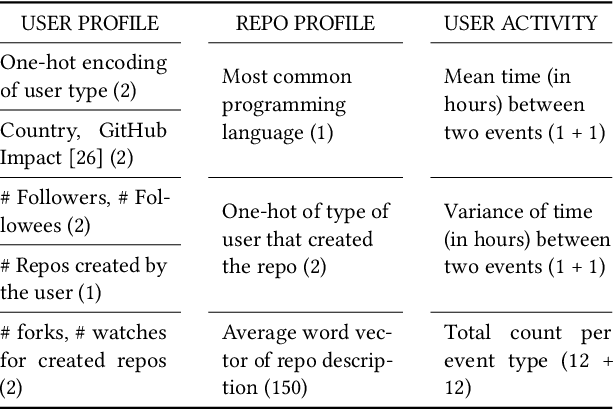
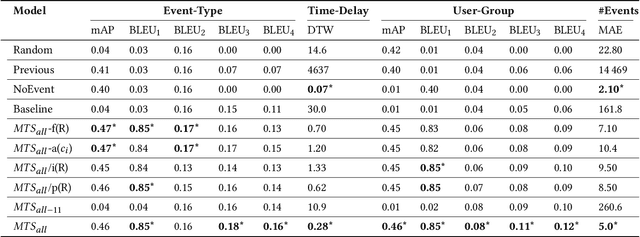
Software development is becoming increasingly open and collaborative with the advent of platforms such as GitHub. Given its crucial role, there is a need to better understand and model the dynamics of GitHub as a social platform. Previous work has mostly considered the dynamics of traditional social networking sites like Twitter and Facebook. We propose GitEvolve, a system to predict the evolution of GitHub repositories and the different ways by which users interact with them. To this end, we develop an end-to-end multi-task sequential deep neural network that given some seed events, simultaneously predicts which user-group is next going to interact with a given repository, what the type of the interaction is, and when it happens. To facilitate learning, we use graph based representation learning to encode relationship between repositories. We map users to groups by modelling common interests to better predict popularity and to generalize to unseen users during inference. We introduce an artificial event type to better model varying levels of activity of repositories in the dataset. The proposed multi-task architecture is generic and can be extended to model information diffusion in other social networks. In a series of experiments, we demonstrate the effectiveness of the proposed model, using multiple metrics and baselines. Qualitative analysis of the model's ability to predict popularity and forecast trends proves its applicability.

Heuristic Framework for Multi-Scale Testing of the Multi-Manifold Hypothesis

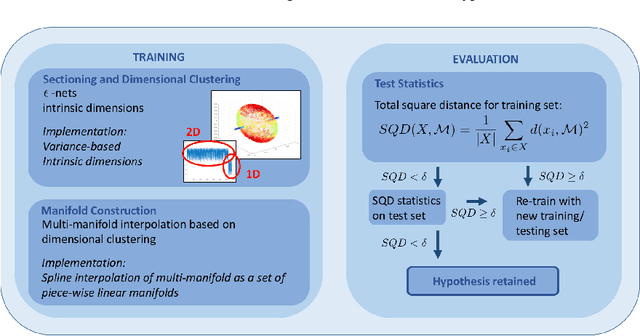
When analyzing empirical data, we often find that global linear models overestimate the number of parameters required. In such cases, we may ask whether the data lies on or near a manifold or a set of manifolds (a so-called multi-manifold) of lower dimension than the ambient space. This question can be phrased as a (multi-) manifold hypothesis. The identification of such intrinsic multiscale features is a cornerstone of data analysis and representation and has given rise to a large body of work on manifold learning. In this work, we review key results on multi-scale data analysis and intrinsic dimension followed by the introduction of a heuristic, multiscale framework for testing the multi-manifold hypothesis. Our method implements a hypothesis test on a set of spline-interpolated manifolds constructed from variance-based intrinsic dimensions. The workflow is suitable for empirical data analysis as we demonstrate on two use cases.

Multi-Scale Local Shape Analysis and Feature Selection in Machine Learning Applications

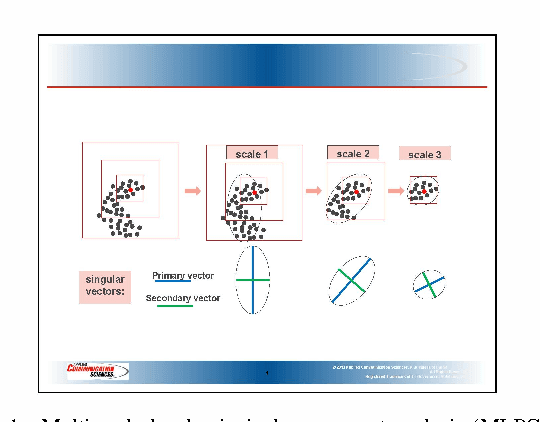
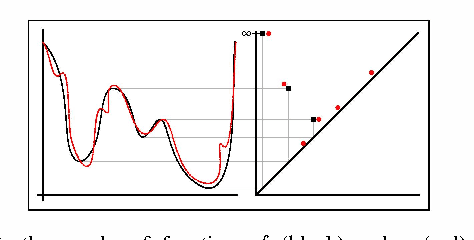
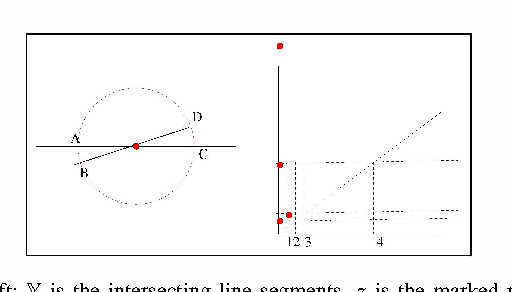
We introduce a method called multi-scale local shape analysis, or MLSA, for extracting features that describe the local structure of points within a dataset. The method uses both geometric and topological features at multiple levels of granularity to capture diverse types of local information for subsequent machine learning algorithms operating on the dataset. Using synthetic and real dataset examples, we demonstrate significant performance improvement of classification algorithms constructed for these datasets with correspondingly augmented features.