Machine Learning in LiDAR 3D point clouds

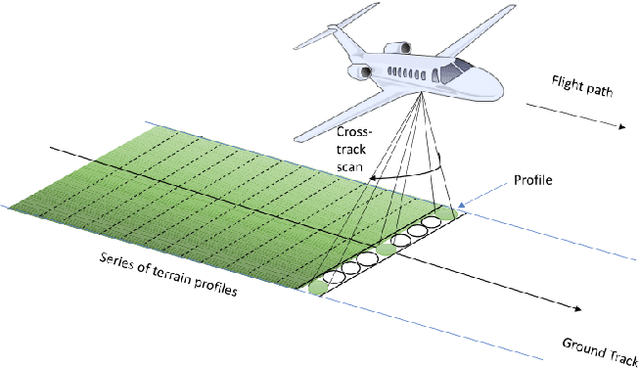
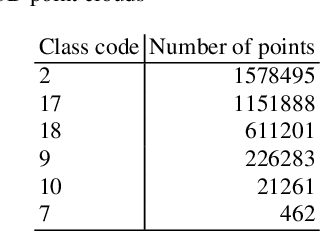
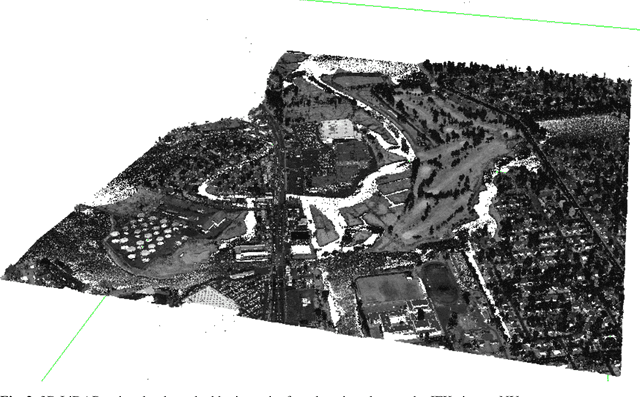
LiDAR point clouds contain measurements of complicated natural scenes and can be used to update digital elevation models, glacial monitoring, detecting faults and measuring uplift detecting, forest inventory, detect shoreline and beach volume changes, landslide risk analysis, habitat mapping, and urban development, among others. A very important application is the classification of the 3D cloud into elementary classes. For example, it can be used to differentiate between vegetation, man-made structures, and water. Our goal is to present a preliminary comparison study for the classification of 3D point cloud LiDAR data that includes several types of feature engineering. In particular, we demonstrate that providing context by augmenting each point in the LiDAR point cloud with information about its neighboring points can improve the performance of downstream learning algorithms. We also experiment with several dimension reduction strategies, ranging from Principal Component Analysis (PCA) to neural network-based auto-encoders, and demonstrate how they affect classification performance in LiDAR point clouds. For instance, we observe that combining feature engineering with a dimension reduction a method such as PCA, there is an improvement in the accuracy of the classification with respect to doing a straightforward classification with the raw data.

Heuristic Framework for Multi-Scale Testing of the Multi-Manifold Hypothesis

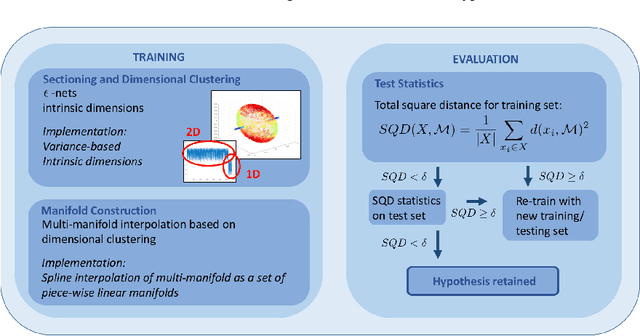
When analyzing empirical data, we often find that global linear models overestimate the number of parameters required. In such cases, we may ask whether the data lies on or near a manifold or a set of manifolds (a so-called multi-manifold) of lower dimension than the ambient space. This question can be phrased as a (multi-) manifold hypothesis. The identification of such intrinsic multiscale features is a cornerstone of data analysis and representation and has given rise to a large body of work on manifold learning. In this work, we review key results on multi-scale data analysis and intrinsic dimension followed by the introduction of a heuristic, multiscale framework for testing the multi-manifold hypothesis. Our method implements a hypothesis test on a set of spline-interpolated manifolds constructed from variance-based intrinsic dimensions. The workflow is suitable for empirical data analysis as we demonstrate on two use cases.