Power Spectrum Signatures of Graphs

Point signatures based on the Laplacian operators on graphs, point clouds, and manifolds have become popular tools in machine learning for graphs, clustering, and shape analysis. In this work, we propose a novel point signature, the power spectrum signature, a measure on $\mathbb{R}$ defined as the squared graph Fourier transform of a graph signal. Unlike eigenvectors of the Laplacian from which it is derived, the power spectrum signature is invariant under graph automorphisms. We show that the power spectrum signature is stable under perturbations of the input graph with respect to the Wasserstein metric. We focus on the signature applied to classes of indicator functions, and its applications to generating descriptive features for vertices of graphs. To demonstrate the practical value of our signature, we showcase several applications in characterizing geometry and symmetries in point cloud data, and graph regression problems.

Heuristic Framework for Multi-Scale Testing of the Multi-Manifold Hypothesis

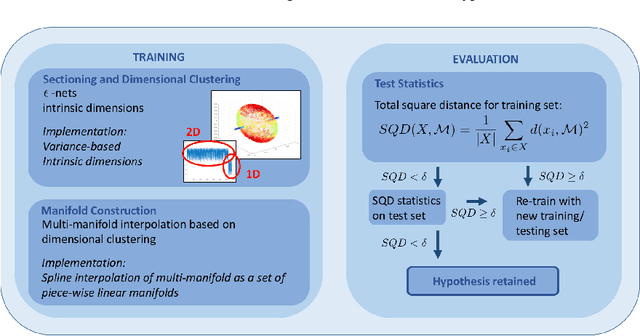
When analyzing empirical data, we often find that global linear models overestimate the number of parameters required. In such cases, we may ask whether the data lies on or near a manifold or a set of manifolds (a so-called multi-manifold) of lower dimension than the ambient space. This question can be phrased as a (multi-) manifold hypothesis. The identification of such intrinsic multiscale features is a cornerstone of data analysis and representation and has given rise to a large body of work on manifold learning. In this work, we review key results on multi-scale data analysis and intrinsic dimension followed by the introduction of a heuristic, multiscale framework for testing the multi-manifold hypothesis. Our method implements a hypothesis test on a set of spline-interpolated manifolds constructed from variance-based intrinsic dimensions. The workflow is suitable for empirical data analysis as we demonstrate on two use cases.