Power Spectrum Signatures of Graphs

Point signatures based on the Laplacian operators on graphs, point clouds, and manifolds have become popular tools in machine learning for graphs, clustering, and shape analysis. In this work, we propose a novel point signature, the power spectrum signature, a measure on $\mathbb{R}$ defined as the squared graph Fourier transform of a graph signal. Unlike eigenvectors of the Laplacian from which it is derived, the power spectrum signature is invariant under graph automorphisms. We show that the power spectrum signature is stable under perturbations of the input graph with respect to the Wasserstein metric. We focus on the signature applied to classes of indicator functions, and its applications to generating descriptive features for vertices of graphs. To demonstrate the practical value of our signature, we showcase several applications in characterizing geometry and symmetries in point cloud data, and graph regression problems.

Optimisation of Spectral Wavelets for Persistence-based Graph Classification

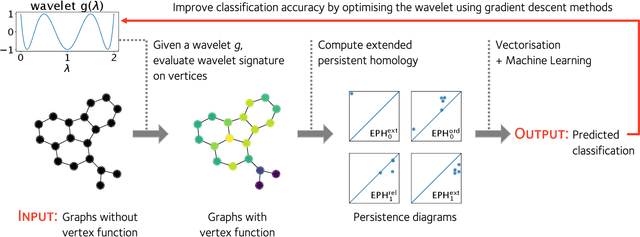
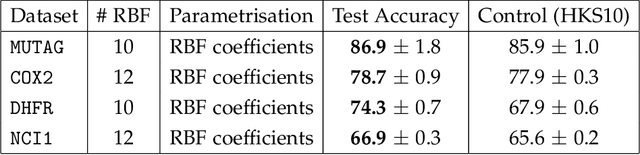
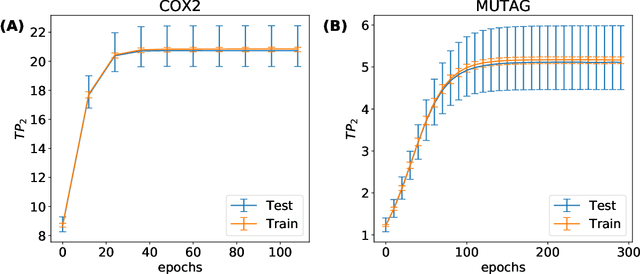
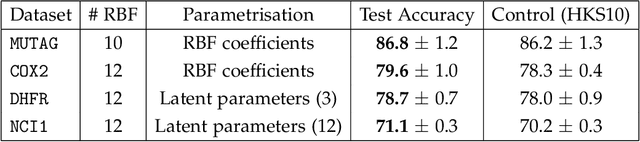
A graph's spectral wavelet signature determines a filtration, and consequently an associated set of extended persistence diagrams. We propose a framework that optimises the choice of wavelet for a dataset of graphs, such that their associated persistence diagrams capture features of the graphs that are best suited to a given data science problem. Since the spectral wavelet signature of a graph is derived from its Laplacian, our framework encodes geometric properties of graphs in their associated persistence diagrams and can be applied to graphs without a priori vertex features. We demonstrate how our framework can be coupled with different persistence diagram vectorisation methods for various supervised and unsupervised learning problems, such as graph classification and finding persistence maximising filtrations, respectively. To provide the underlying theoretical foundations, we extend the differentiability result for ordinary persistent homology to extended persistent homology.