Jacob Leygonie
DATASHAPE
A Gradient Sampling Algorithm for Stratified Maps with Applications to Topological Data Analysis
Sep 03, 2021

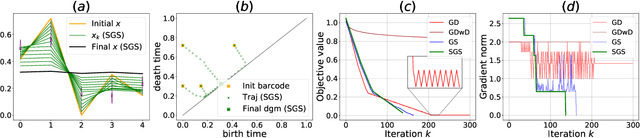
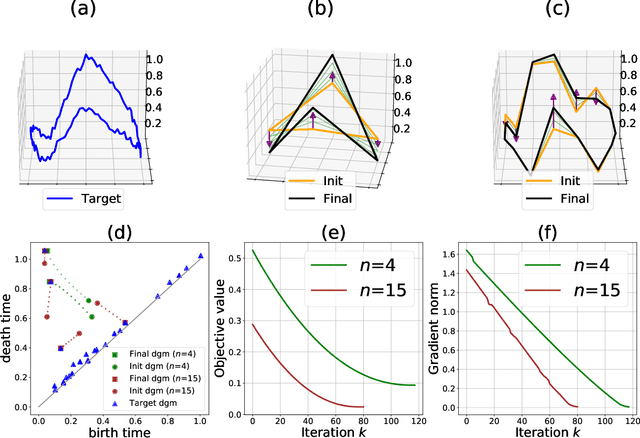
Abstract:We introduce a novel gradient descent algorithm extending the well-known Gradient Sampling methodology to the class of stratifiably smooth objective functions, which are defined as locally Lipschitz functions that are smooth on some regular pieces-called the strata-of the ambient Euclidean space. For this class of functions, our algorithm achieves a sub-linear convergence rate. We then apply our method to objective functions based on the (extended) persistent homology map computed over lower-star filters, which is a central tool of Topological Data Analysis. For this, we propose an efficient exploration of the corresponding stratification by using the Cayley graph of the permutation group. Finally, we provide benchmark and novel topological optimization problems, in order to demonstrate the utility and applicability of our framework.
Optimisation of Spectral Wavelets for Persistence-based Graph Classification
Jan 10, 2021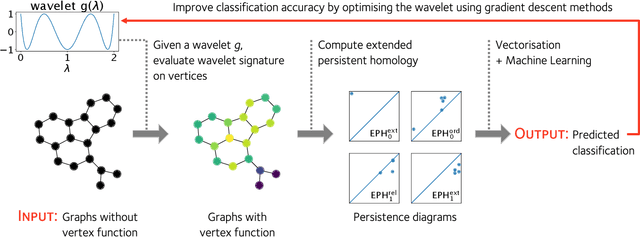
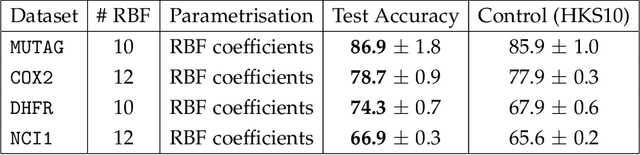
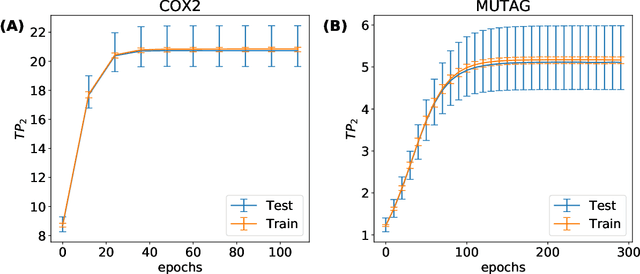
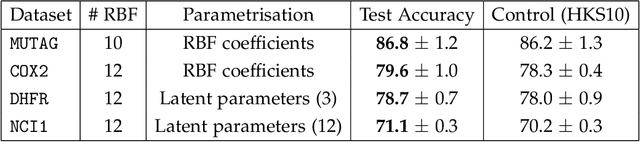
Abstract:A graph's spectral wavelet signature determines a filtration, and consequently an associated set of extended persistence diagrams. We propose a framework that optimises the choice of wavelet for a dataset of graphs, such that their associated persistence diagrams capture features of the graphs that are best suited to a given data science problem. Since the spectral wavelet signature of a graph is derived from its Laplacian, our framework encodes geometric properties of graphs in their associated persistence diagrams and can be applied to graphs without a priori vertex features. We demonstrate how our framework can be coupled with different persistence diagram vectorisation methods for various supervised and unsupervised learning problems, such as graph classification and finding persistence maximising filtrations, respectively. To provide the underlying theoretical foundations, we extend the differentiability result for ordinary persistent homology to extended persistent homology.
Adversarial Computation of Optimal Transport Maps
Jun 24, 2019
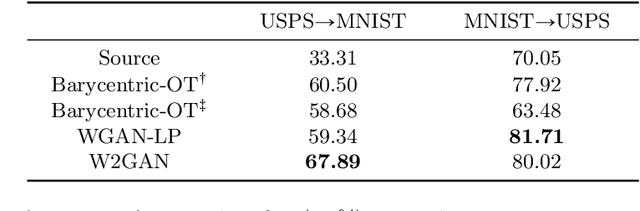
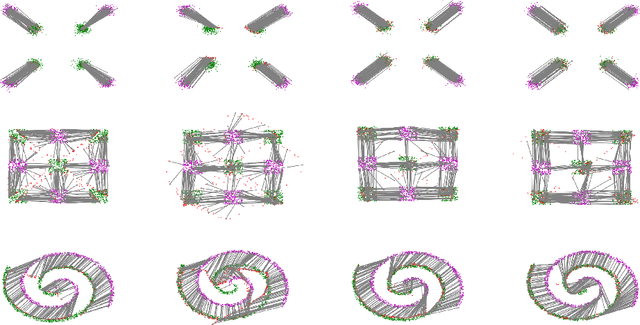
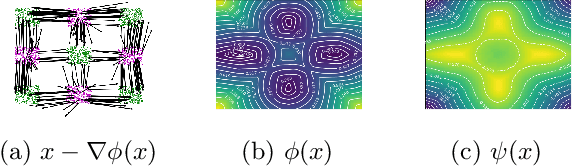
Abstract:Computing optimal transport maps between high-dimensional and continuous distributions is a challenging problem in optimal transport (OT). Generative adversarial networks (GANs) are powerful generative models which have been successfully applied to learn maps across high-dimensional domains. However, little is known about the nature of the map learned with a GAN objective. To address this problem, we propose a generative adversarial model in which the discriminator's objective is the $2$-Wasserstein metric. We show that during training, our generator follows the $W_2$-geodesic between the initial and the target distributions. As a consequence, it reproduces an optimal map at the end of training. We validate our approach empirically in both low-dimensional and high-dimensional continuous settings, and show that it outperforms prior methods on image data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge