ADAPT: Multimodal Learning for Detecting Physiological Changes under Missing Modalities

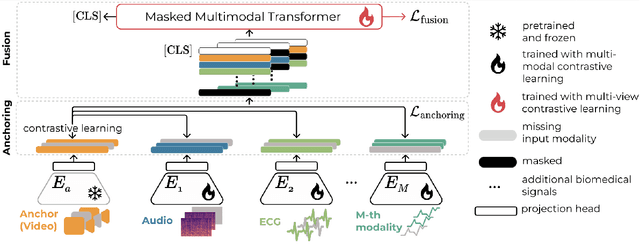
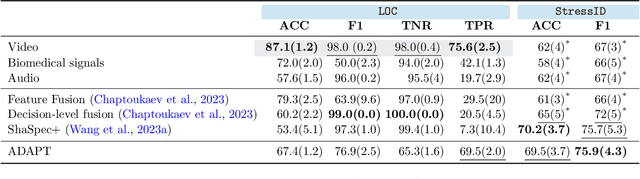
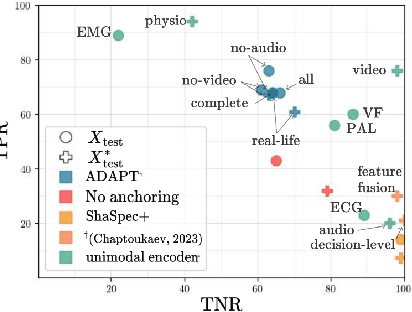
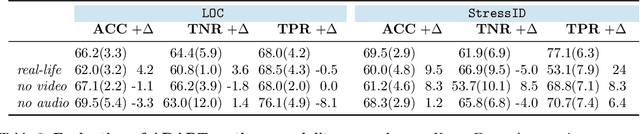
Multimodality has recently gained attention in the medical domain, where imaging or video modalities may be integrated with biomedical signals or health records. Yet, two challenges remain: balancing the contributions of modalities, especially in cases with a limited amount of data available, and tackling missing modalities. To address both issues, in this paper, we introduce the AnchoreD multimodAl Physiological Transformer (ADAPT), a multimodal, scalable framework with two key components: (i) aligning all modalities in the space of the strongest, richest modality (called anchor) to learn a joint embedding space, and (ii) a Masked Multimodal Transformer, leveraging both inter- and intra-modality correlations while handling missing modalities. We focus on detecting physiological changes in two real-life scenarios: stress in individuals induced by specific triggers and fighter pilots' loss of consciousness induced by $g$-forces. We validate the generalizability of ADAPT through extensive experiments on two datasets for these tasks, where we set the new state of the art while demonstrating its robustness across various modality scenarios and its high potential for real-life applications.

D-GRIL: End-to-End Topological Learning with 2-parameter Persistence

End-to-end topological learning using 1-parameter persistence is well-known. We show that the framework can be enhanced using 2-parameter persistence by adopting a recently introduced 2-parameter persistence based vectorization technique called GRIL. We establish a theoretical foundation of differentiating GRIL producing D-GRIL. We show that D-GRIL can be used to learn a bifiltration function on standard benchmark graph datasets. Further, we exhibit that this framework can be applied in the context of bio-activity prediction in drug discovery.

Stable Vectorization of Multiparameter Persistent Homology using Signed Barcodes as Measures

Persistent homology (PH) provides topological descriptors for geometric data, such as weighted graphs, which are interpretable, stable to perturbations, and invariant under, e.g., relabeling. Most applications of PH focus on the one-parameter case -- where the descriptors summarize the changes in topology of data as it is filtered by a single quantity of interest -- and there is now a wide array of methods enabling the use of one-parameter PH descriptors in data science, which rely on the stable vectorization of these descriptors as elements of a Hilbert space. Although the multiparameter PH (MPH) of data that is filtered by several quantities of interest encodes much richer information than its one-parameter counterpart, the scarceness of stability results for MPH descriptors has so far limited the available options for the stable vectorization of MPH. In this paper, we aim to bring together the best of both worlds by showing how the interpretation of signed barcodes -- a recent family of MPH descriptors -- as signed measures leads to natural extensions of vectorization strategies from one parameter to multiple parameters. The resulting feature vectors are easy to define and to compute, and provably stable. While, as a proof of concept, we focus on simple choices of signed barcodes and vectorizations, we already see notable performance improvements when comparing our feature vectors to state-of-the-art topology-based methods on various types of data.

A Gradient Sampling Algorithm for Stratified Maps with Applications to Topological Data Analysis

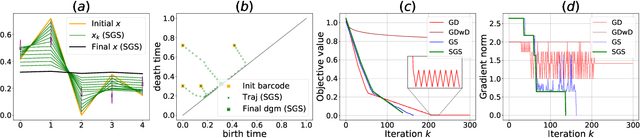
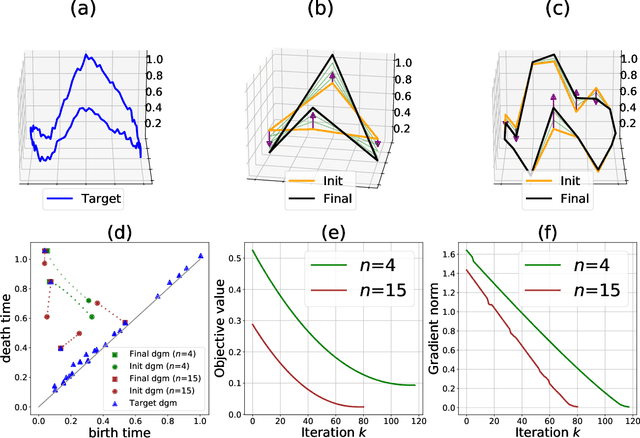
We introduce a novel gradient descent algorithm extending the well-known Gradient Sampling methodology to the class of stratifiably smooth objective functions, which are defined as locally Lipschitz functions that are smooth on some regular pieces-called the strata-of the ambient Euclidean space. For this class of functions, our algorithm achieves a sub-linear convergence rate. We then apply our method to objective functions based on the (extended) persistent homology map computed over lower-star filters, which is a central tool of Topological Data Analysis. For this, we propose an efficient exploration of the corresponding stratification by using the Cayley graph of the permutation group. Finally, we provide benchmark and novel topological optimization problems, in order to demonstrate the utility and applicability of our framework.

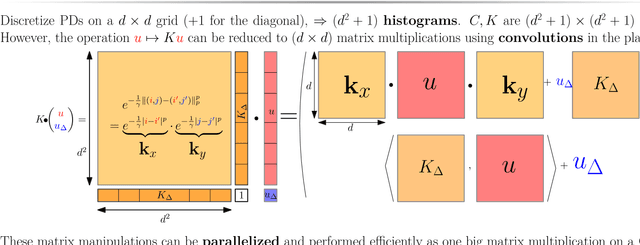
Large Scale computation of Means and Clusters for Persistence Diagrams using Optimal Transport

Persistence diagrams (PDs) are now routinely used to summarize the underlying topology of sophisticated data encountered in challenging learning problems. Despite several appealing properties, integrating PDs in learning pipelines can be challenging because their natural geometry is not Hilbertian. In particular, algorithms to average a family of PDs have only been considered recently and are known to be computationally prohibitive. We propose in this article a tractable framework to carry out fundamental tasks on PDs, namely evaluating distances, computing barycenters and carrying out clustering. This framework builds upon a formulation of PD metrics as optimal transport (OT) problems, for which recent computational advances, in particular entropic regularization and its convolutional formulation on regular grids, can all be leveraged to provide efficient and (GPU) scalable computations. We demonstrate the efficiency of our approach by carrying out clustering on PDs at scales never seen before in the literature.

Sliced Wasserstein Kernel for Persistence Diagrams

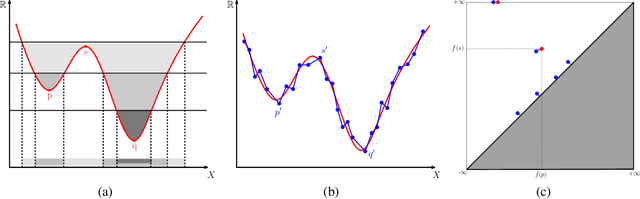
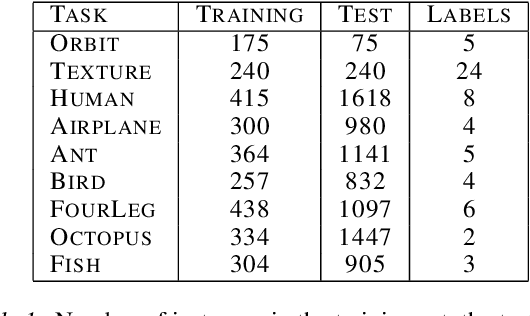
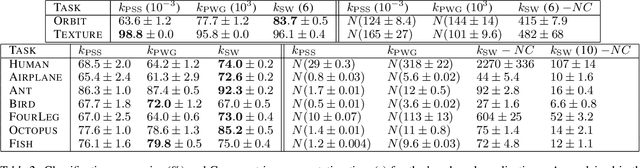
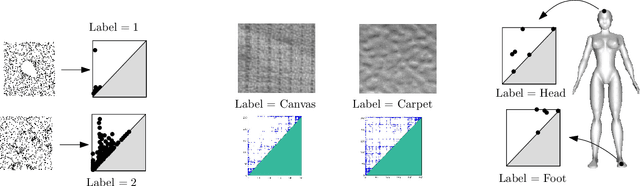
Persistence diagrams (PDs) play a key role in topological data analysis (TDA), in which they are routinely used to describe topological properties of complicated shapes. PDs enjoy strong stability properties and have proven their utility in various learning contexts. They do not, however, live in a space naturally endowed with a Hilbert structure and are usually compared with specific distances, such as the bottleneck distance. To incorporate PDs in a learning pipeline, several kernels have been proposed for PDs with a strong emphasis on the stability of the RKHS distance w.r.t. perturbations of the PDs. In this article, we use the Sliced Wasserstein approximation SW of the Wasserstein distance to define a new kernel for PDs, which is not only provably stable but also provably discriminative (depending on the number of points in the PDs) w.r.t. the Wasserstein distance $d_1$ between PDs. We also demonstrate its practicality, by developing an approximation technique to reduce kernel computation time, and show that our proposal compares favorably to existing kernels for PDs on several benchmarks.

A Fuzzy Clustering Algorithm for the Mode Seeking Framework

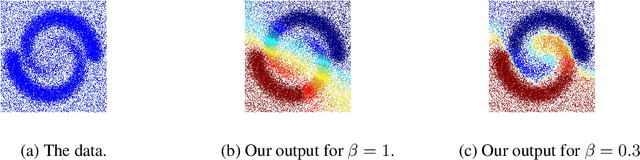
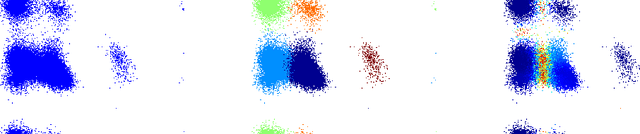
In this paper, we propose a new fuzzy clustering algorithm based on the mode-seeking framework. Given a dataset in $\mathbb{R}^d$, we define regions of high density that we call cluster cores. We then consider a random walk on a neighborhood graph built on top of our data points which is designed to be attracted by high density regions. The strength of this attraction is controlled by a temperature parameter $\beta > 0$. The membership of a point to a given cluster is then the probability for the random walk to hit the corresponding cluster core before any other. While many properties of random walks (such as hitting times, commute distances, etc\dots) have been shown to enventually encode purely local information when the number of data points grows, we show that the regularization introduced by the use of cluster cores solves this issue. Empirically, we show how the choice of $\beta$ influences the behavior of our algorithm: for small values of $\beta$ the result is close to hard mode-seeking whereas when $\beta$ is close to $1$ the result is similar to the output of a (fuzzy) spectral clustering. Finally, we demonstrate the scalability of our approach by providing the fuzzy clustering of a protein configuration dataset containing a million data points in $30$ dimensions.