Thomas Bonis
Random walks on simplicial complexes
Apr 12, 2024



Abstract:The notion of Laplacian of a graph can be generalized to simplicial complexes and hypergraphs, and contains information on the topology of these structures. Even for a graph, the consideration of associated simplicial complexes is interesting to understand its shape. Whereas the Laplacian of a graph has a simple probabilistic interpretation as the generator of a continuous time Markov chain on the graph, things are not so direct when considering simplicial complexes. We define here new Markov chains on simplicial complexes. For a given order~$k$, the state space is the set of $k$-cycles that are chains of $k$-simplexes with null boundary. This new framework is a natural generalization of the canonical Markov chains on graphs. We show that the generator of our Markov chain is the upper Laplacian defined in the context of algebraic topology for discrete structure. We establish several key properties of this new process: in particular, when the number of vertices is finite, the Markov chain is positive recurrent. This result is not trivial, since the cycles can loop over themselves an unbounded number of times. We study the diffusive limits when the simplicial complexes under scrutiny are a sequence of ever refining triangulations of the flat torus. Using the analogy between singular and Hodge homologies, we express this limit as valued in the set of currents. The proof of tightness and the identification of the limiting martingale problem make use of the flat norm and carefully controls of the error terms in the convergence of the generator. Uniqueness of the solution to the martingale problem is left open. An application to hole detection is carried.
Topological phase estimation method for reparameterized periodic functions
May 28, 2022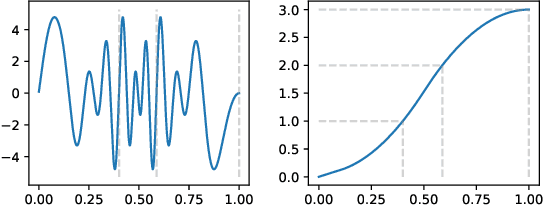
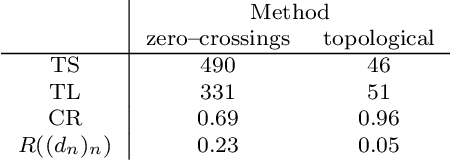
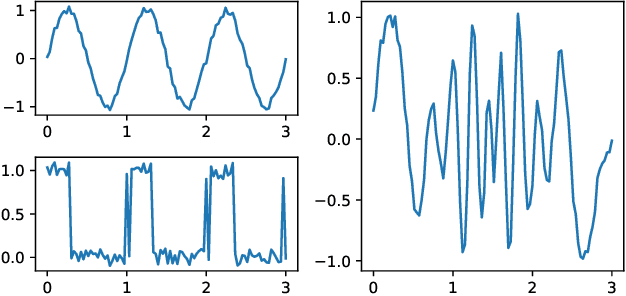
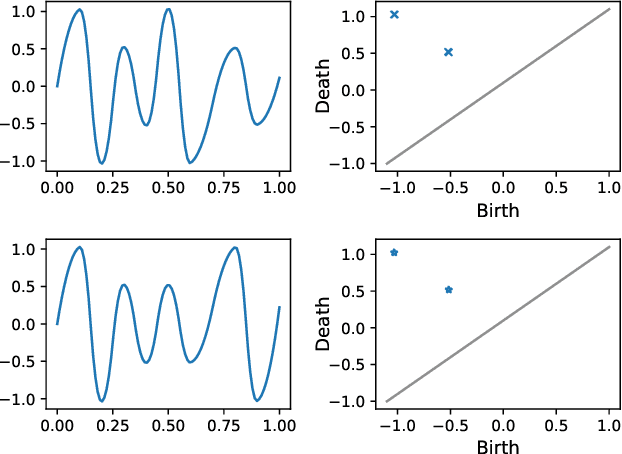
Abstract:We consider a signal composed of several periods of a periodic function, of which we observe a noisy reparametrisation. The phase estimation problem consists of finding that reparametrisation, and, in particular, the number of observed periods. Existing methods are well-suited to the setting where the periodic function is known, or at least, simple. We consider the case when it is unknown and we propose an estimation method based on the shape of the signal. We use the persistent homology of sublevel sets of the signal to capture the temporal structure of its local extrema. We infer the number of periods in the signal by counting points in the persistence diagram and their multiplicities. Using the estimated number of periods, we construct an estimator of the reparametrisation. It is based on counting the number of sufficiently prominent local minima in the signal. This work is motivated by a vehicle positioning problem, on which we evaluated the proposed method.
Guarantees in Wasserstein Distance for the Langevin Monte Carlo Algorithm
Jul 01, 2016Abstract:We study the problem of sampling from a distribution $\target$ using the Langevin Monte Carlo algorithm and provide rate of convergences for this algorithm in terms of Wasserstein distance of order $2$. Our result holds as long as the continuous diffusion process associated with the algorithm converges exponentially fast to the target distribution along with some technical assumptions. While such an exponential convergence holds for example in the log-concave measure case, it also holds for the more general case of asymptoticaly log-concave measures. Our results thus extends the known rates of convergence in total variation and Wasserstein distances which have only been obtained in the log-concave case. Moreover, using a sharper approximation bound of the continuous process, we obtain better asymptotic rates than traditional results. We also look into variations of the Langevin Monte Carlo algorithm using other discretization schemes. In a first time, we look into the use of the Ozaki's discretization but are unable to obtain any significative improvement in terms of convergence rates compared to the Euler's scheme. We then provide a (sub-optimal) way to study more general schemes, however our approach only holds for the log-concave case.
A Fuzzy Clustering Algorithm for the Mode Seeking Framework
Jun 22, 2016
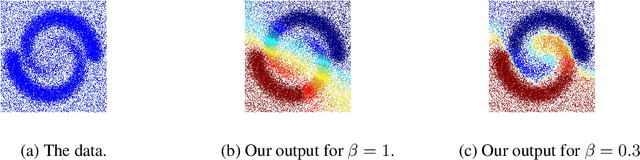
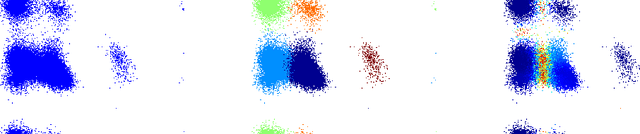
Abstract:In this paper, we propose a new fuzzy clustering algorithm based on the mode-seeking framework. Given a dataset in $\mathbb{R}^d$, we define regions of high density that we call cluster cores. We then consider a random walk on a neighborhood graph built on top of our data points which is designed to be attracted by high density regions. The strength of this attraction is controlled by a temperature parameter $\beta > 0$. The membership of a point to a given cluster is then the probability for the random walk to hit the corresponding cluster core before any other. While many properties of random walks (such as hitting times, commute distances, etc\dots) have been shown to enventually encode purely local information when the number of data points grows, we show that the regularization introduced by the use of cluster cores solves this issue. Empirically, we show how the choice of $\beta$ influences the behavior of our algorithm: for small values of $\beta$ the result is close to hard mode-seeking whereas when $\beta$ is close to $1$ the result is similar to the output of a (fuzzy) spectral clustering. Finally, we demonstrate the scalability of our approach by providing the fuzzy clustering of a protein configuration dataset containing a million data points in $30$ dimensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge