Stable Vectorization of Multiparameter Persistent Homology using Signed Barcodes as Measures

Persistent homology (PH) provides topological descriptors for geometric data, such as weighted graphs, which are interpretable, stable to perturbations, and invariant under, e.g., relabeling. Most applications of PH focus on the one-parameter case -- where the descriptors summarize the changes in topology of data as it is filtered by a single quantity of interest -- and there is now a wide array of methods enabling the use of one-parameter PH descriptors in data science, which rely on the stable vectorization of these descriptors as elements of a Hilbert space. Although the multiparameter PH (MPH) of data that is filtered by several quantities of interest encodes much richer information than its one-parameter counterpart, the scarceness of stability results for MPH descriptors has so far limited the available options for the stable vectorization of MPH. In this paper, we aim to bring together the best of both worlds by showing how the interpretation of signed barcodes -- a recent family of MPH descriptors -- as signed measures leads to natural extensions of vectorization strategies from one parameter to multiple parameters. The resulting feature vectors are easy to define and to compute, and provably stable. While, as a proof of concept, we focus on simple choices of signed barcodes and vectorizations, we already see notable performance improvements when comparing our feature vectors to state-of-the-art topology-based methods on various types of data.

Toroidal Coordinates: Decorrelating Circular Coordinates With Lattice Reduction

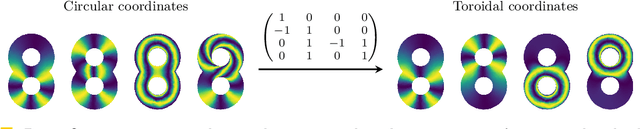
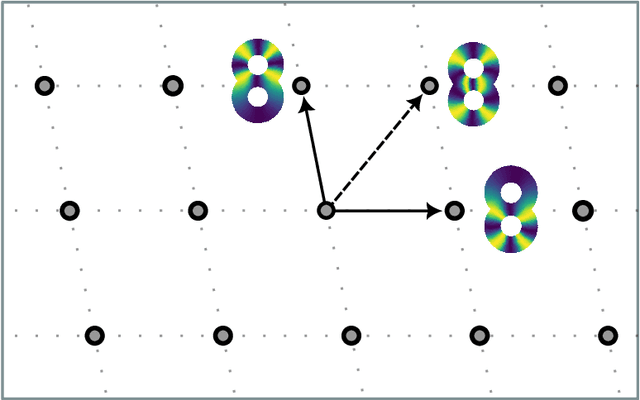
The circular coordinates algorithm of de Silva, Morozov, and Vejdemo-Johansson takes as input a dataset together with a cohomology class representing a $1$-dimensional hole in the data; the output is a map from the data into the circle that captures this hole, and that is of minimum energy in a suitable sense. However, when applied to several cohomology classes, the output circle-valued maps can be "geometrically correlated" even if the chosen cohomology classes are linearly independent. It is shown in the original work that less correlated maps can be obtained with suitable integer linear combinations of the cohomology classes, with the linear combinations being chosen by inspection. In this paper, we identify a formal notion of geometric correlation between circle-valued maps which, in the Riemannian manifold case, corresponds to the Dirichlet form, a bilinear form derived from the Dirichlet energy. We describe a systematic procedure for constructing low energy torus-valued maps on data, starting from a set of linearly independent cohomology classes. We showcase our procedure with computational examples. Our main algorithm is based on the Lenstra--Lenstra--Lov\'asz algorithm from computational number theory.

Fiberwise dimensionality reduction of topologically complex data with vector bundles

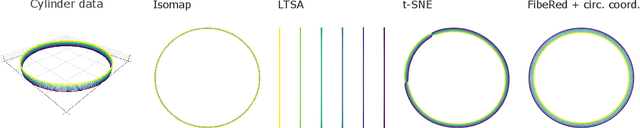
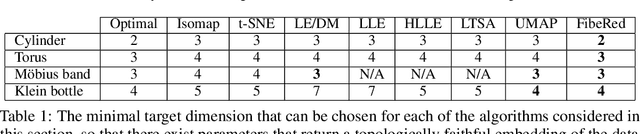
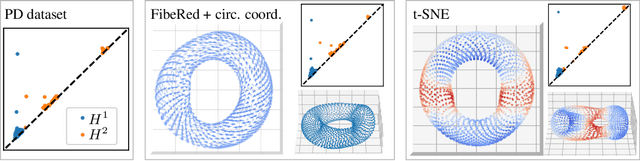
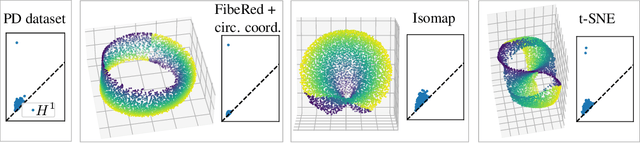
Datasets with non-trivial large scale topology can be hard to embed in low-dimensional Euclidean space with existing dimensionality reduction algorithms. We propose to model topologically complex datasets using vector bundles, in such a way that the base space accounts for the large scale topology, while the fibers account for the local geometry. This allows one to reduce the dimensionality of the fibers, while preserving the large scale topology. We formalize this point of view, and, as an application, we describe an algorithm which takes as input a dataset together with an initial representation of it in Euclidean space, assumed to recover part of its large scale topology, and outputs a new representation that integrates local representations, obtained through local linear dimensionality reduction, along the initial global representation. We demonstrate this algorithm on examples coming from dynamical systems and chemistry. In these examples, our algorithm is able to learn topologically faithful embeddings of the data in lower target dimension than various well known metric-based dimensionality reduction algorithms.

Stable and consistent density-based clustering

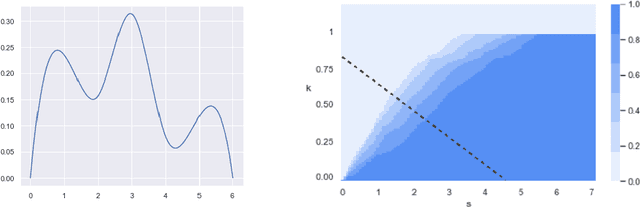
We present a consistent approach to density-based clustering, which satisfies a stability theorem that holds without any distributional assumptions. We also show that the algorithm can be combined with standard procedures to extract a flat clustering from a hierarchical clustering, and that the resulting flat clustering algorithms satisfy stability theorems. The algorithms and proofs are inspired by topological data analysis.

Spaces of Clusterings

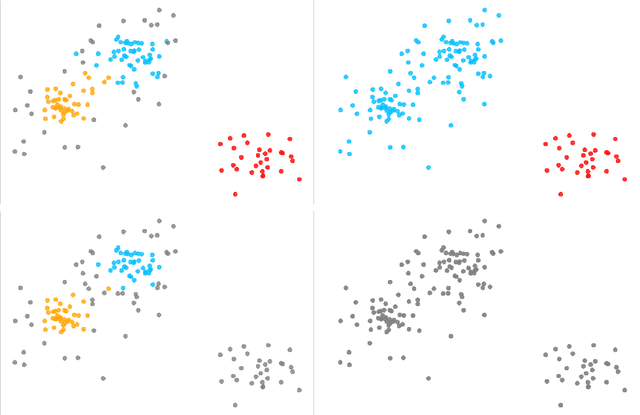
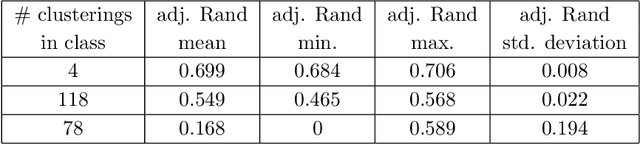
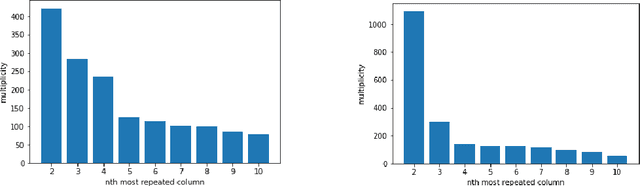
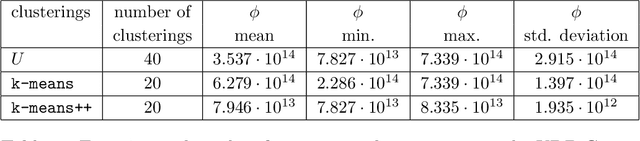
We propose two algorithms to cluster a set of clusterings of a fixed dataset, such as sets of clusterings produced by running a clustering algorithm with a range of parameters, or with many initializations. We use these to study the effects of varying the parameters of HDBSCAN, and to study methods for initializing $k$-means.