$O(k)$-Equivariant Dimensionality Reduction on Stiefel Manifolds

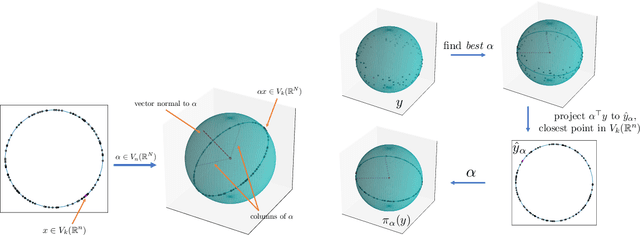
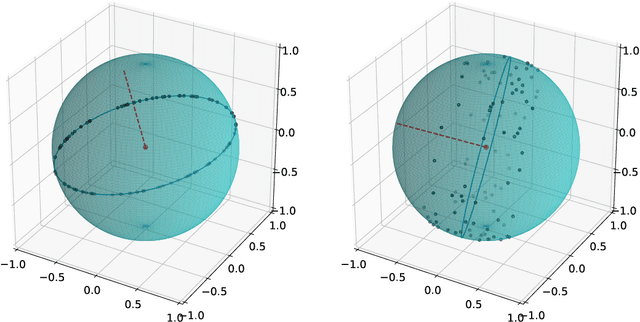
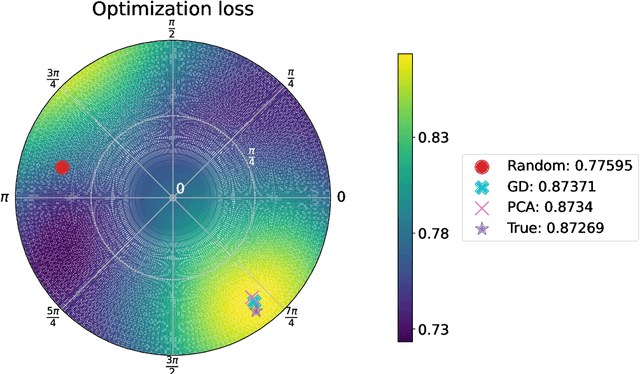
Many real-world datasets live on high-dimensional Stiefel and Grassmannian manifolds, $V_k(\mathbb{R}^N)$ and $Gr(k, \mathbb{R}^N)$ respectively, and benefit from projection onto lower-dimensional Stiefel (respectively, Grassmannian) manifolds. In this work, we propose an algorithm called Principal Stiefel Coordinates (PSC) to reduce data dimensionality from $ V_k(\mathbb{R}^N)$ to $V_k(\mathbb{R}^n)$ in an $O(k)$-equivariant manner ($k \leq n \ll N$). We begin by observing that each element $\alpha \in V_n(\mathbb{R}^N)$ defines an isometric embedding of $V_k(\mathbb{R}^n)$ into $V_k(\mathbb{R}^N)$. Next, we optimize for such an embedding map that minimizes data fit error by warm-starting with the output of principal component analysis (PCA) and applying gradient descent. Then, we define a continuous and $O(k)$-equivariant map $\pi_\alpha$ that acts as a ``closest point operator'' to project the data onto the image of $V_k(\mathbb{R}^n)$ in $V_k(\mathbb{R}^N)$ under the embedding determined by $\alpha$, while minimizing distortion. Because this dimensionality reduction is $O(k)$-equivariant, these results extend to Grassmannian manifolds as well. Lastly, we show that the PCA output globally minimizes projection error in a noiseless setting, but that our algorithm achieves a meaningfully different and improved outcome when the data does not lie exactly on the image of a linearly embedded lower-dimensional Stiefel manifold as above. Multiple numerical experiments using synthetic and real-world data are performed.

Learning on Persistence Diagrams as Radon Measures

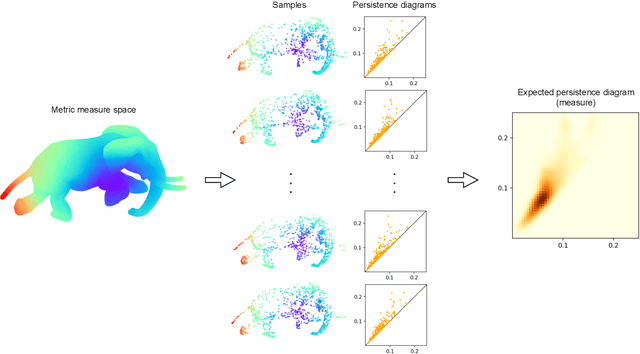
Persistence diagrams are common descriptors of the topological structure of data appearing in various classification and regression tasks. They can be generalized to Radon measures supported on the birth-death plane and endowed with an optimal transport distance. Examples of such measures are expectations of probability distributions on the space of persistence diagrams. In this paper, we develop methods for approximating continuous functions on the space of Radon measures supported on the birth-death plane, as well as their utilization in supervised learning tasks. Indeed, we show that any continuous function defined on a compact subset of the space of such measures (e.g., a classifier or regressor) can be approximated arbitrarily well by polynomial combinations of features computed using a continuous compactly supported function on the birth-death plane (a template). We provide insights into the structure of relatively compact subsets of the space of Radon measures, and test our approximation methodology on various data sets and supervised learning tasks.

Toroidal Coordinates: Decorrelating Circular Coordinates With Lattice Reduction

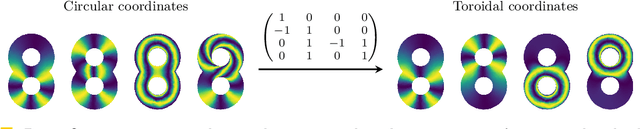
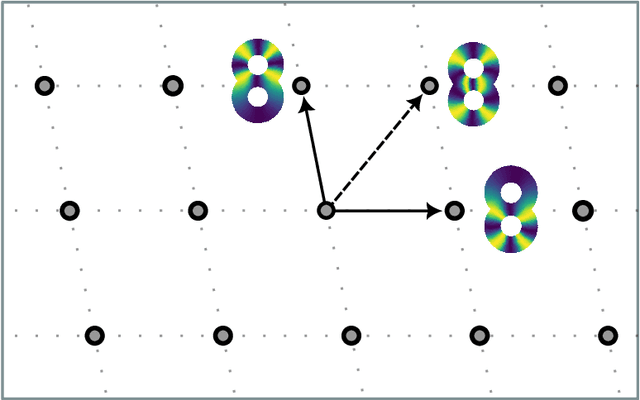
The circular coordinates algorithm of de Silva, Morozov, and Vejdemo-Johansson takes as input a dataset together with a cohomology class representing a $1$-dimensional hole in the data; the output is a map from the data into the circle that captures this hole, and that is of minimum energy in a suitable sense. However, when applied to several cohomology classes, the output circle-valued maps can be "geometrically correlated" even if the chosen cohomology classes are linearly independent. It is shown in the original work that less correlated maps can be obtained with suitable integer linear combinations of the cohomology classes, with the linear combinations being chosen by inspection. In this paper, we identify a formal notion of geometric correlation between circle-valued maps which, in the Riemannian manifold case, corresponds to the Dirichlet form, a bilinear form derived from the Dirichlet energy. We describe a systematic procedure for constructing low energy torus-valued maps on data, starting from a set of linearly independent cohomology classes. We showcase our procedure with computational examples. Our main algorithm is based on the Lenstra--Lenstra--Lov\'asz algorithm from computational number theory.

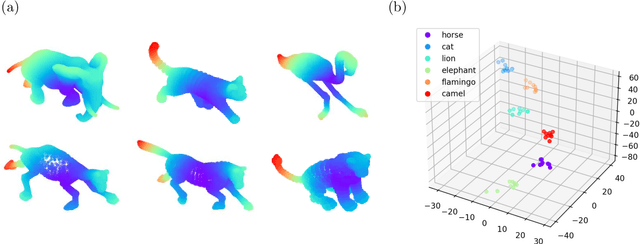
Fiberwise dimensionality reduction of topologically complex data with vector bundles

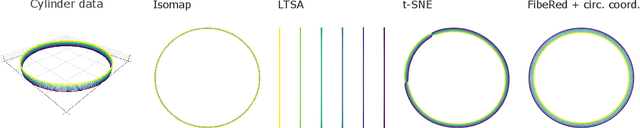
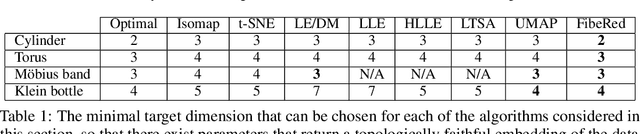
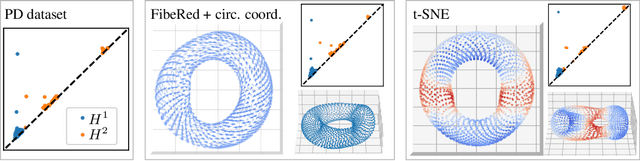
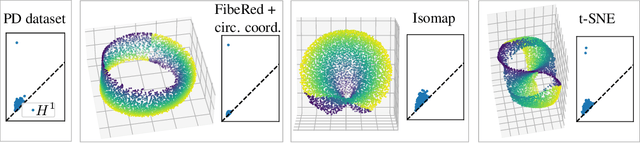
Datasets with non-trivial large scale topology can be hard to embed in low-dimensional Euclidean space with existing dimensionality reduction algorithms. We propose to model topologically complex datasets using vector bundles, in such a way that the base space accounts for the large scale topology, while the fibers account for the local geometry. This allows one to reduce the dimensionality of the fibers, while preserving the large scale topology. We formalize this point of view, and, as an application, we describe an algorithm which takes as input a dataset together with an initial representation of it in Euclidean space, assumed to recover part of its large scale topology, and outputs a new representation that integrates local representations, obtained through local linear dimensionality reduction, along the initial global representation. We demonstrate this algorithm on examples coming from dynamical systems and chemistry. In these examples, our algorithm is able to learn topologically faithful embeddings of the data in lower target dimension than various well known metric-based dimensionality reduction algorithms.

Adaptive template systems: Data-driven feature selection for learning with persistence diagrams

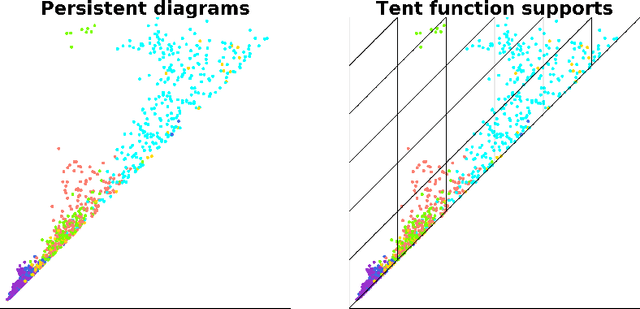
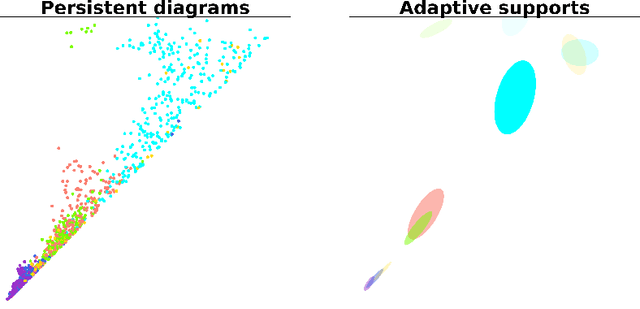
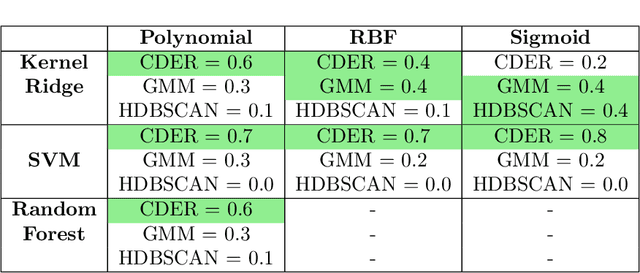
Feature extraction from persistence diagrams, as a tool to enrich machine learning techniques, has received increasing attention in recent years. In this paper we explore an adaptive methodology to localize features in persistent diagrams, which are then used in learning tasks. Specifically, we investigate three algorithms, CDER, GMM and HDBSCAN, to obtain adaptive template functions/features. Said features are evaluated in three classification experiments with persistence diagrams. Namely, manifold, human shapes and protein classification. The main conclusion of our analysis is that adaptive template systems, as a feature extraction technique, yield competitive and often superior results in the studied examples. Moreover, from the adaptive algorithms here studied, CDER consistently provides the most reliable and robust adaptive featurization.

Approximating Continuous Functions on Persistence Diagrams Using Template Functions

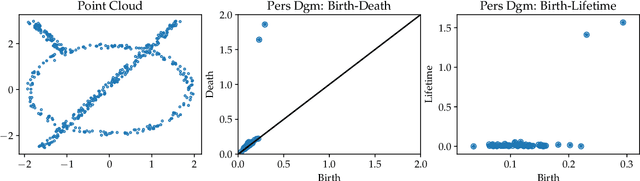
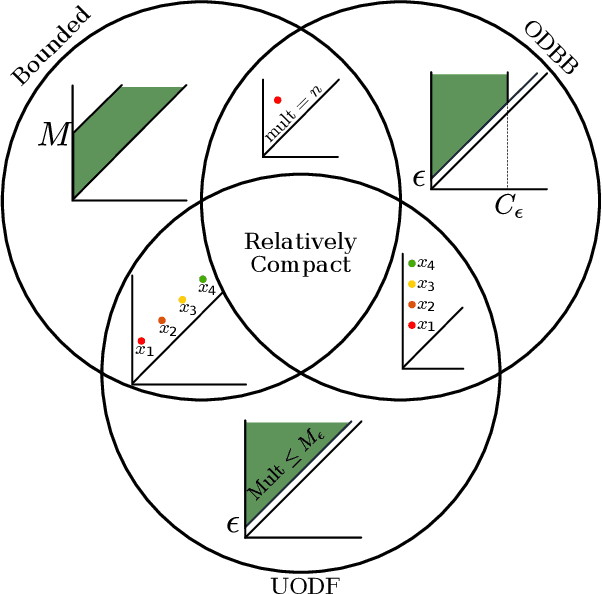
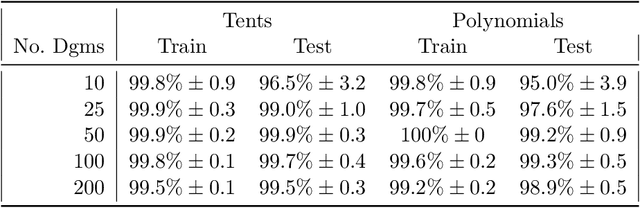
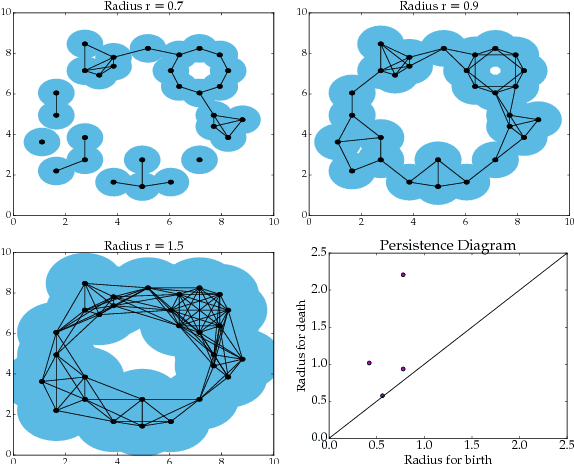
The persistence diagram is an increasingly useful tool from Topological Data Analysis, but its use alongside typical machine learning techniques requires mathematical finesse. The most success to date has come from methods that map persistence diagrams into $\mathbb{R}^n$, in a way which maximizes the structure preserved. This process is commonly referred to as featurization. In this paper, we describe a mathematical framework for featurization using template functions. These functions are general as they are only required to be continuous and compactly supported. We discuss two realizations: tent functions, which emphasize the local contributions of points in a persistence diagram, and interpolating polynomials, which capture global pairwise interactions. We combine the resulting features with classification and regression algorithms on several examples including shape data and the Rossler system. Our results show that using template functions yields high accuracy rates that match and often exceed those of existing featurization methods. One counter-intuitive observation is that in most cases using interpolating polynomials, where each point contributes globally to the feature vector, yields significantly better results than using tent functions, where the contribution of each point is localized. Along the way, we provide a complete characterization of compactness in the space of persistence diagrams.

Chatter Classification in Turning Using Machine Learning and Topological Data Analysis

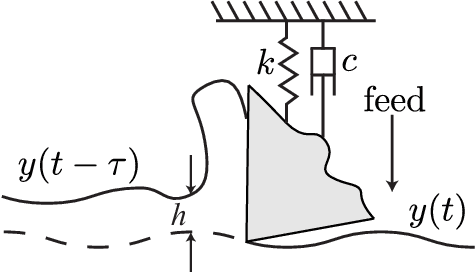
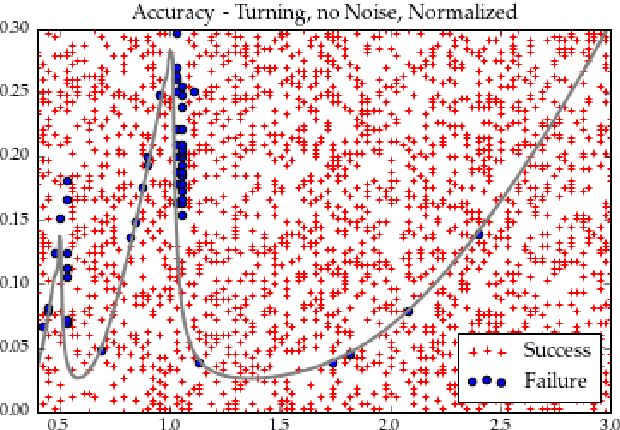
Chatter identification and detection in machining processes has been an active area of research in the past two decades. Part of the challenge in studying chatter is that machining equations that describe its occurrence are often nonlinear delay differential equations. The majority of the available tools for chatter identification rely on defining a metric that captures the characteristics of chatter, and a threshold that signals its occurrence. The difficulty in choosing these parameters can be somewhat alleviated by utilizing machine learning techniques. However, even with a successful classification algorithm, the transferability of typical machine learning methods from one data set to another remains very limited. In this paper we combine supervised machine learning with Topological Data Analysis (TDA) to obtain a descriptor of the process which can detect chatter. The features we use are derived from the persistence diagram of an attractor reconstructed from the time series via Takens embedding. We test the approach using deterministic and stochastic turning models, where the stochasticity is introduced via the cutting coefficient term. Our results show a 97% successful classification rate on the deterministic model labeled by the stability diagram obtained using the spectral element method. The features gleaned from the deterministic model are then utilized for characterization of chatter in a stochastic turning model where there are very limited analysis methods.

(Quasi)Periodicity Quantification in Video Data, Using Topology

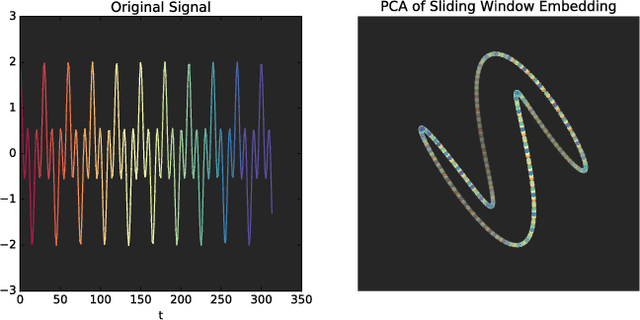
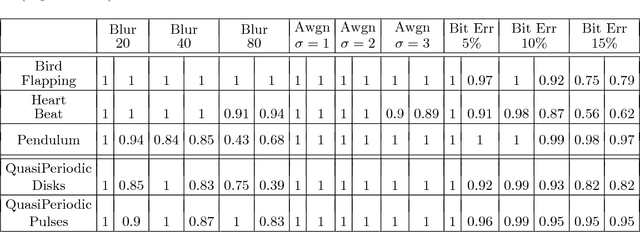
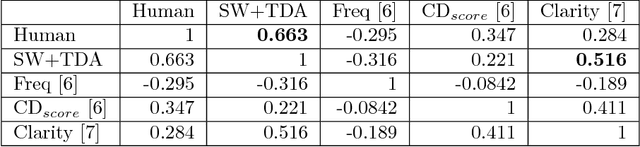
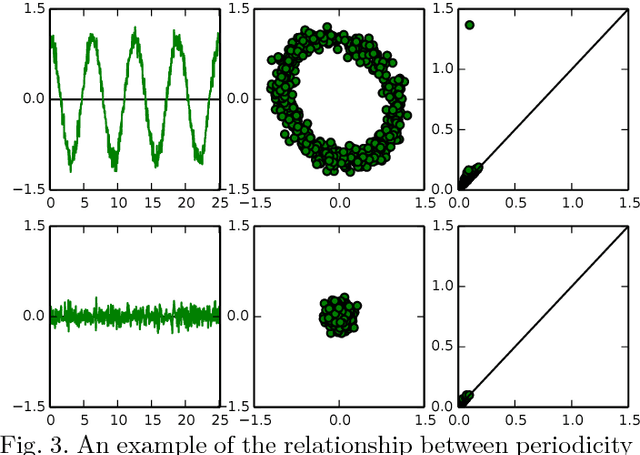
This work introduces a novel framework for quantifying the presence and strength of recurrent dynamics in video data. Specifically, we provide continuous measures of periodicity (perfect repetition) and quasiperiodicity (superposition of periodic modes with non-commensurate periods), in a way which does not require segmentation, training, object tracking or 1-dimensional surrogate signals. Our methodology operates directly on video data. The approach combines ideas from nonlinear time series analysis (delay embeddings) and computational topology (persistent homology), by translating the problem of finding recurrent dynamics in video data, into the problem of determining the circularity or toroidality of an associated geometric space. Through extensive testing, we show the robustness of our scores with respect to several noise models/levels, we show that our periodicity score is superior to other methods when compared to human-generated periodicity rankings, and furthermore, we show that our quasiperiodicity score clearly indicates the presence of biphonation in videos of vibrating vocal folds, which has never before been accomplished end to end quantitatively.