Topological Signatures of ReLU Neural Network Activation Patterns

This paper explores the topological signatures of ReLU neural network activation patterns. We consider feedforward neural networks with ReLU activation functions and analyze the polytope decomposition of the feature space induced by the network. Mainly, we investigate how the Fiedler partition of the dual graph and show that it appears to correlate with the decision boundary -- in the case of binary classification. Additionally, we compute the homology of the cellular decomposition -- in a regression task -- to draw similar patterns in behavior between the training loss and polyhedral cell-count, as the model is trained.

Learning on Persistence Diagrams as Radon Measures

Persistence diagrams are common descriptors of the topological structure of data appearing in various classification and regression tasks. They can be generalized to Radon measures supported on the birth-death plane and endowed with an optimal transport distance. Examples of such measures are expectations of probability distributions on the space of persistence diagrams. In this paper, we develop methods for approximating continuous functions on the space of Radon measures supported on the birth-death plane, as well as their utilization in supervised learning tasks. Indeed, we show that any continuous function defined on a compact subset of the space of such measures (e.g., a classifier or regressor) can be approximated arbitrarily well by polynomial combinations of features computed using a continuous compactly supported function on the birth-death plane (a template). We provide insights into the structure of relatively compact subsets of the space of Radon measures, and test our approximation methodology on various data sets and supervised learning tasks.

Toroidal Coordinates: Decorrelating Circular Coordinates With Lattice Reduction

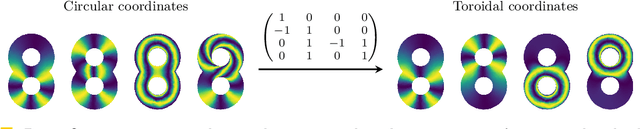
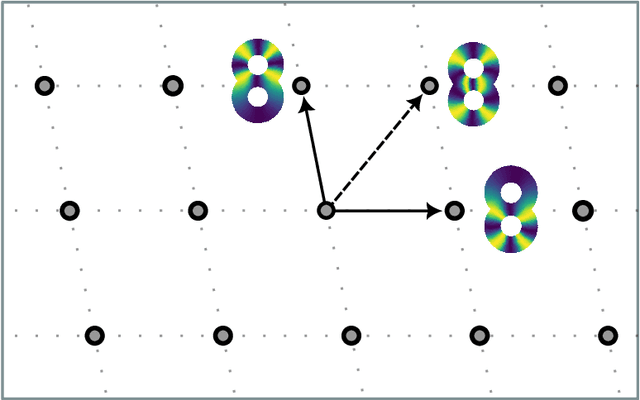
The circular coordinates algorithm of de Silva, Morozov, and Vejdemo-Johansson takes as input a dataset together with a cohomology class representing a $1$-dimensional hole in the data; the output is a map from the data into the circle that captures this hole, and that is of minimum energy in a suitable sense. However, when applied to several cohomology classes, the output circle-valued maps can be "geometrically correlated" even if the chosen cohomology classes are linearly independent. It is shown in the original work that less correlated maps can be obtained with suitable integer linear combinations of the cohomology classes, with the linear combinations being chosen by inspection. In this paper, we identify a formal notion of geometric correlation between circle-valued maps which, in the Riemannian manifold case, corresponds to the Dirichlet form, a bilinear form derived from the Dirichlet energy. We describe a systematic procedure for constructing low energy torus-valued maps on data, starting from a set of linearly independent cohomology classes. We showcase our procedure with computational examples. Our main algorithm is based on the Lenstra--Lenstra--Lov\'asz algorithm from computational number theory.