Toroidal Coordinates: Decorrelating Circular Coordinates With Lattice Reduction

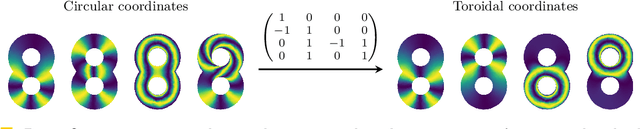
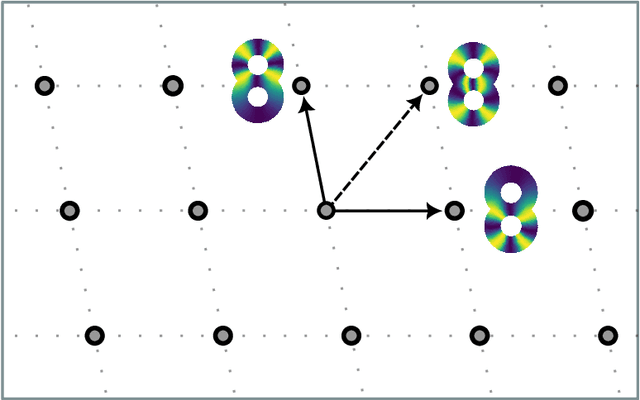
The circular coordinates algorithm of de Silva, Morozov, and Vejdemo-Johansson takes as input a dataset together with a cohomology class representing a $1$-dimensional hole in the data; the output is a map from the data into the circle that captures this hole, and that is of minimum energy in a suitable sense. However, when applied to several cohomology classes, the output circle-valued maps can be "geometrically correlated" even if the chosen cohomology classes are linearly independent. It is shown in the original work that less correlated maps can be obtained with suitable integer linear combinations of the cohomology classes, with the linear combinations being chosen by inspection. In this paper, we identify a formal notion of geometric correlation between circle-valued maps which, in the Riemannian manifold case, corresponds to the Dirichlet form, a bilinear form derived from the Dirichlet energy. We describe a systematic procedure for constructing low energy torus-valued maps on data, starting from a set of linearly independent cohomology classes. We showcase our procedure with computational examples. Our main algorithm is based on the Lenstra--Lenstra--Lov\'asz algorithm from computational number theory.

On the Nonlinear Statistics of Optical Flow

In "A naturalistic open source movie for optical flow evaluation," Butler et al. create a database of ground-truth optical flow from the computer-generated video Sintel. We study the high-contrast $3\times 3$ patches from this video, and provide evidence that this dataset is well-modeled by a torus (a nonlinear 2-dimensional manifold). Our main tools are persistent homology and zigzag persistence, which are popular techniques from the field of computational topology. We show that the optical flow torus model is naturally equipped with the structure of a fiber bundle, which is furthermore related to the statistics of range images.