A Primer on Topological Data Analysis to Support Image Analysis Tasks in Environmental Science

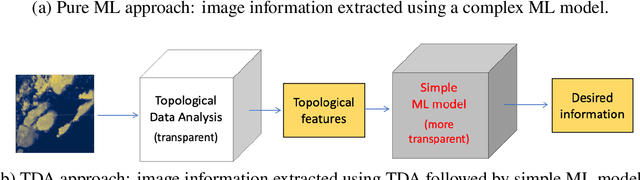
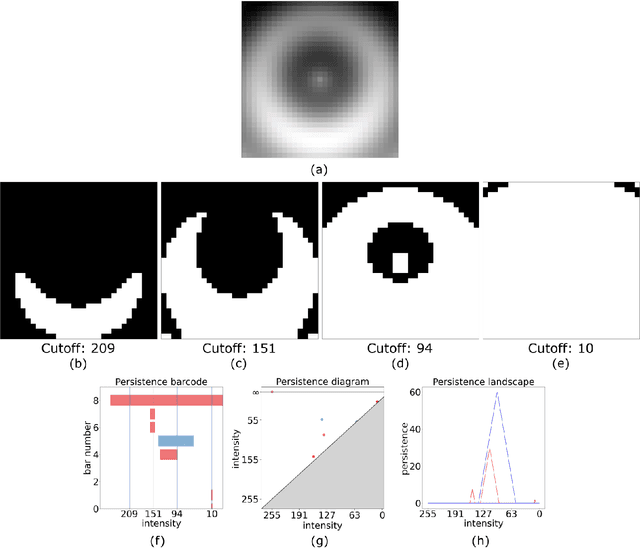
Topological data analysis (TDA) is a tool from data science and mathematics that is beginning to make waves in environmental science. In this work, we seek to provide an intuitive and understandable introduction to a tool from TDA that is particularly useful for the analysis of imagery, namely persistent homology. We briefly discuss the theoretical background but focus primarily on understanding the output of this tool and discussing what information it can glean. To this end, we frame our discussion around a guiding example of classifying satellite images from the Sugar, Fish, Flower, and Gravel Dataset produced for the study of mesocale organization of clouds by Rasp et. al. in 2020 (arXiv:1906:01906). We demonstrate how persistent homology and its vectorization, persistence landscapes, can be used in a workflow with a simple machine learning algorithm to obtain good results, and explore in detail how we can explain this behavior in terms of image-level features. One of the core strengths of persistent homology is how interpretable it can be, so throughout this paper we discuss not just the patterns we find, but why those results are to be expected given what we know about the theory of persistent homology. Our goal is that a reader of this paper will leave with a better understanding of TDA and persistent homology, be able to identify problems and datasets of their own for which persistent homology could be helpful, and gain an understanding of results they obtain from applying the included GitHub example code.

Topology Applied to Machine Learning: From Global to Local

Through the use of examples, we explain one way in which applied topology has evolved since the birth of persistent homology in the early 2000s. The first applications of topology to data emphasized the global shape of a dataset, such as the three-circle model for $3 \times 3$ pixel patches from natural images, or the configuration space of the cyclo-octane molecule, which is a sphere with a Klein bottle attached via two circles of singularity. In these studies of global shape, short persistent homology bars are disregarded as sampling noise. More recently, however, persistent homology has been used to address questions about the local geometry of data. For instance, how can local geometry be vectorized for use in machine learning problems? Persistent homology and its vectorization methods, including persistence landscapes and persistence images, provide popular techniques for incorporating both local geometry and global topology into machine learning. Our meta-hypothesis is that the short bars are as important as the long bars for many machine learning tasks. In defense of this claim, we survey applications of persistent homology to shape recognition, agent-based modeling, materials science, archaeology, and biology. Additionally, we survey work connecting persistent homology to geometric features of spaces, including curvature and fractal dimension, and various methods that have been used to incorporate persistent homology into machine learning.

Support Vector Machines and Radon's Theorem

A support vector machine (SVM) is an algorithm which finds a hyperplane that optimally separates labeled data points in $\mathbb{R}^n$ into positive and negative classes. The data points on the margin of this separating hyperplane are called support vectors. We study the possible configurations of support vectors for points in general position. In particular, we connect the possible configurations to Radon's theorem, which provides guarantees for when a set of points can be divided into two classes (positive and negative) whose convex hulls intersect. If the positive and negative support vectors in a generic SVM configuration are projected to the separating hyperplane, then these projected points will form a Radon configuration. Further, with a particular type of general position, we show there are at most $n+1$ support vectors. This can be used to test the level of machine precision needed in a support vector machine implementation. We also show the projections of the convex hulls of the support vectors intersect in a single Radon point, and under a small enough perturbation, the points labeled as support vectors remain labeled as support vectors. We furthermore consider computations studying the expected number of support vectors for randomly generated data.

Capturing Dynamics of Time-Varying Data via Topology

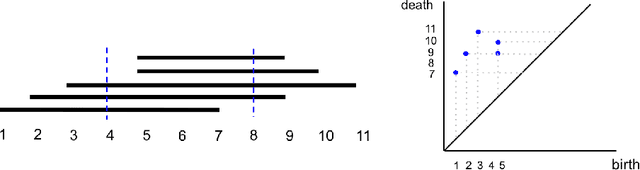
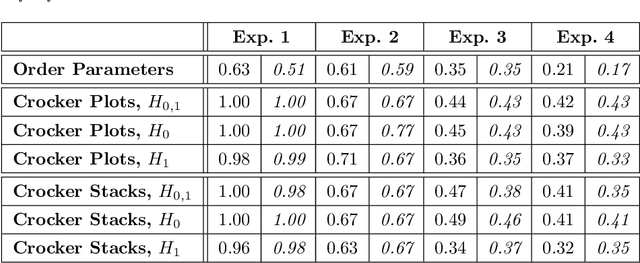
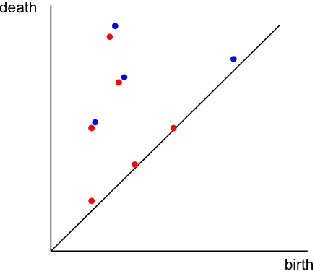
One approach to understanding complex data is to study its shape through the lens of algebraic topology. While the early development of topological data analysis focused primarily on static data, in recent years, theoretical and applied studies have turned to data that varies in time. A time-varying collection of metric spaces as formed, for example, by a moving school of fish or flock of birds, can contain a vast amount of information. There is often a need to simplify or summarize the dynamic behavior. We provide an introduction to topological summaries of time-varying metric spaces including vineyards [17], crocker plots [52], and multiparameter rank functions [34]. We then introduce a new tool to summarize time-varying metric spaces: a crocker stack. Crocker stacks are convenient for visualization, amenable to machine learning, and satisfy a desirable stability property which we prove. We demonstrate the utility of crocker stacks for a parameter identification task involving an influential model of biological aggregations [54]. Altogether, we aim to bring the broader applied mathematics community up-to-date on topological summaries of time-varying metric spaces.

On the Nonlinear Statistics of Optical Flow

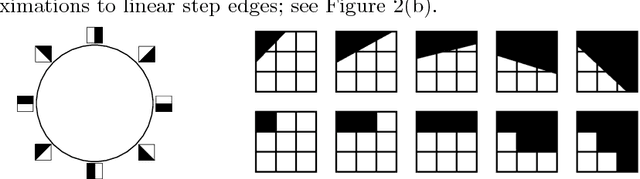
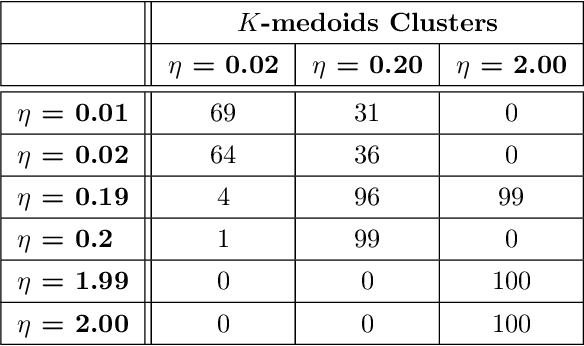
In "A naturalistic open source movie for optical flow evaluation," Butler et al. create a database of ground-truth optical flow from the computer-generated video Sintel. We study the high-contrast $3\times 3$ patches from this video, and provide evidence that this dataset is well-modeled by a torus (a nonlinear 2-dimensional manifold). Our main tools are persistent homology and zigzag persistence, which are popular techniques from the field of computational topology. We show that the optical flow torus model is naturally equipped with the structure of a fiber bundle, which is furthermore related to the statistics of range images.

Persistence Images: A Stable Vector Representation of Persistent Homology

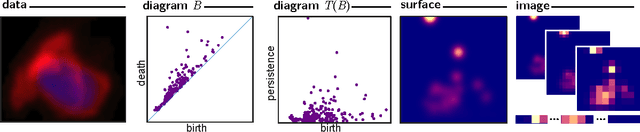
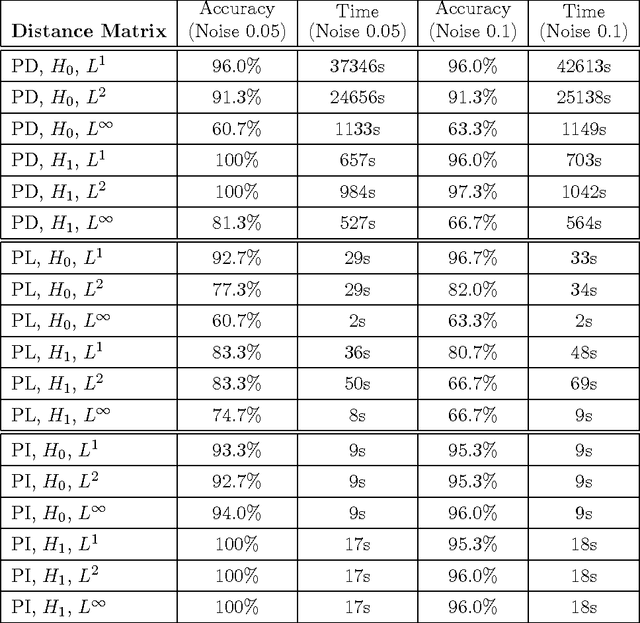
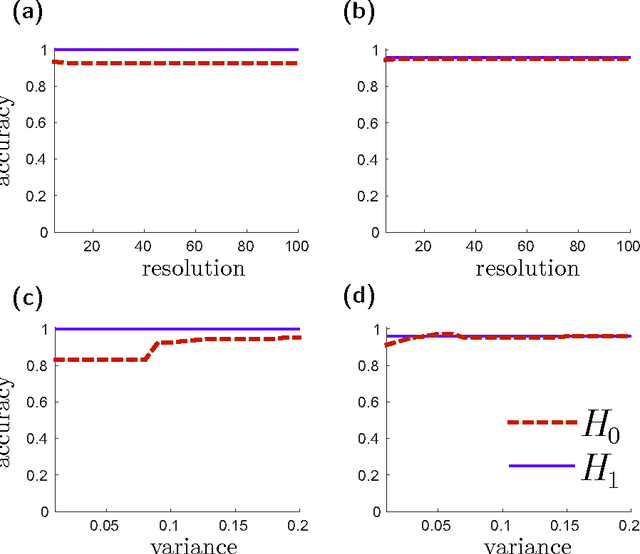
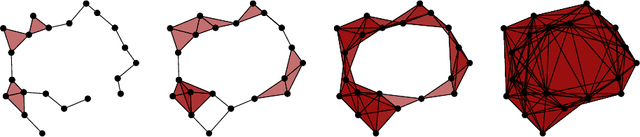
Many datasets can be viewed as a noisy sampling of an underlying space, and tools from topological data analysis can characterize this structure for the purpose of knowledge discovery. One such tool is persistent homology, which provides a multiscale description of the homological features within a dataset. A useful representation of this homological information is a persistence diagram (PD). Efforts have been made to map PDs into spaces with additional structure valuable to machine learning tasks. We convert a PD to a finite-dimensional vector representation which we call a persistence image (PI), and prove the stability of this transformation with respect to small perturbations in the inputs. The discriminatory power of PIs is compared against existing methods, showing significant performance gains. We explore the use of PIs with vector-based machine learning tools, such as linear sparse support vector machines, which identify features containing discriminating topological information. Finally, high accuracy inference of parameter values from the dynamic output of a discrete dynamical system (the linked twist map) and a partial differential equation (the anisotropic Kuramoto-Sivashinsky equation) provide a novel application of the discriminatory power of PIs.

Evasion Paths in Mobile Sensor Networks

Suppose that ball-shaped sensors wander in a bounded domain. A sensor doesn't know its location but does know when it overlaps a nearby sensor. We say that an evasion path exists in this sensor network if a moving intruder can avoid detection. In "Coordinate-free coverage in sensor networks with controlled boundaries via homology", Vin deSilva and Robert Ghrist give a necessary condition, depending only on the time-varying connectivity data of the sensors, for an evasion path to exist. Using zigzag persistent homology, we provide an equivalent condition that moreover can be computed in a streaming fashion. However, no method with time-varying connectivity data as input can give necessary and sufficient conditions for the existence of an evasion path. Indeed, we show that the existence of an evasion path depends not only on the fibrewise homotopy type of the region covered by sensors but also on its embedding in spacetime. For planar sensors that also measure weak rotation and distance information, we provide necessary and sufficient conditions for the existence of an evasion path.