Support Vector Machines and Radon's Theorem

A support vector machine (SVM) is an algorithm which finds a hyperplane that optimally separates labeled data points in $\mathbb{R}^n$ into positive and negative classes. The data points on the margin of this separating hyperplane are called support vectors. We study the possible configurations of support vectors for points in general position. In particular, we connect the possible configurations to Radon's theorem, which provides guarantees for when a set of points can be divided into two classes (positive and negative) whose convex hulls intersect. If the positive and negative support vectors in a generic SVM configuration are projected to the separating hyperplane, then these projected points will form a Radon configuration. Further, with a particular type of general position, we show there are at most $n+1$ support vectors. This can be used to test the level of machine precision needed in a support vector machine implementation. We also show the projections of the convex hulls of the support vectors intersect in a single Radon point, and under a small enough perturbation, the points labeled as support vectors remain labeled as support vectors. We furthermore consider computations studying the expected number of support vectors for randomly generated data.

More chemical detection through less sampling: amplifying chemical signals in hyperspectral data cubes through compressive sensing

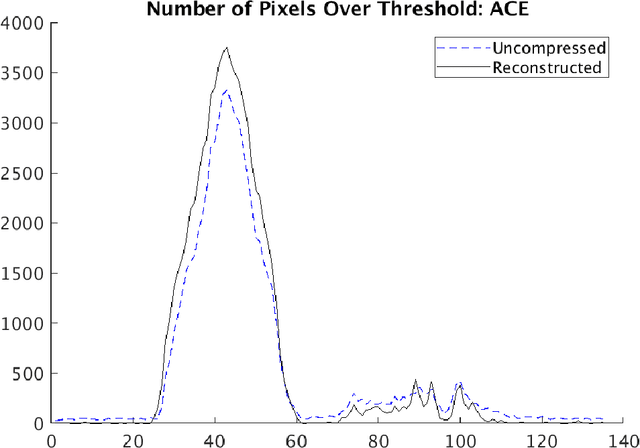
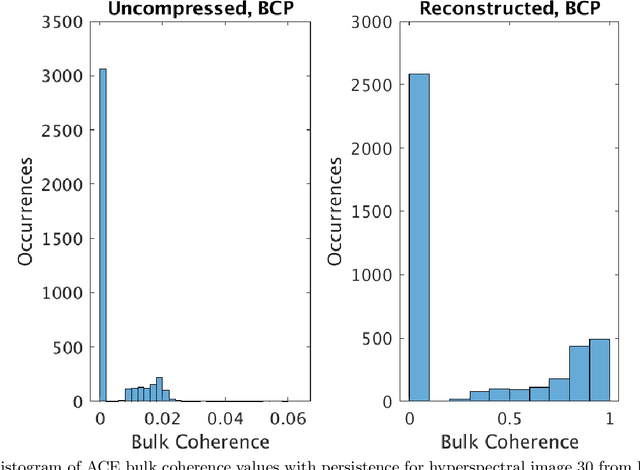
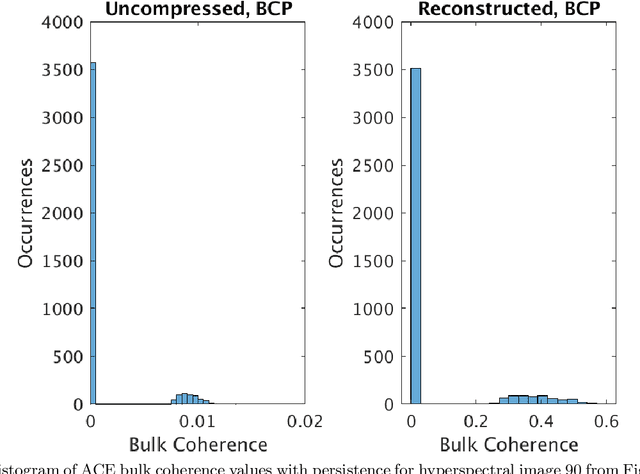
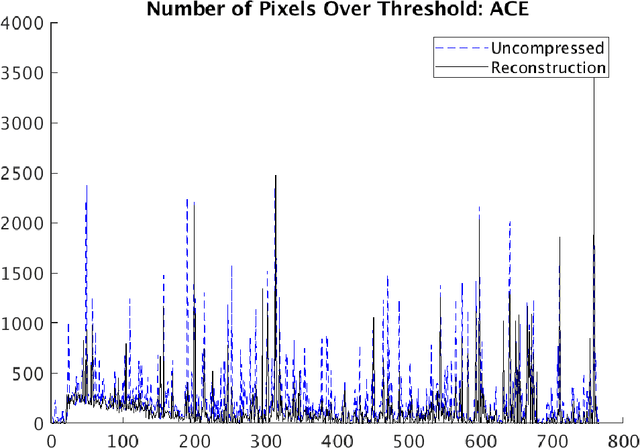
Compressive sensing (CS) is a method of sampling which permits some classes of signals to be reconstructed with high accuracy even when they were under-sampled. In this paper we explore a phenomenon in which bandwise CS sampling of a hyperspectral data cube followed by reconstruction can actually result in amplification of chemical signals contained in the cube. Perhaps most surprisingly, chemical signal amplification generally seems to increase as the level of sampling decreases. In some examples, the chemical signal is significantly stronger in a data cube reconstructed from 10% CS sampling than it is in the raw, 100% sampled data cube. We explore this phenomenon in two real-world datasets including the Physical Sciences Inc. Fabry-P\'{e}rot interferometer sensor multispectral dataset and the Johns Hopkins Applied Physics Lab FTIR-based longwave infrared sensor hyperspectral dataset. Each of these datasets contains the release of a chemical simulant, such as glacial acetic acid, triethyl phospate, and sulfur hexafluoride, and in all cases we use the adaptive coherence estimator (ACE) to detect a target signal in the hyperspectral data cube. We end the paper by suggesting some theoretical justifications for why chemical signals would be amplified in CS sampled and reconstructed hyperspectral data cubes and discuss some practical implications.

A data-driven approach to sampling matrix selection for compressive sensing

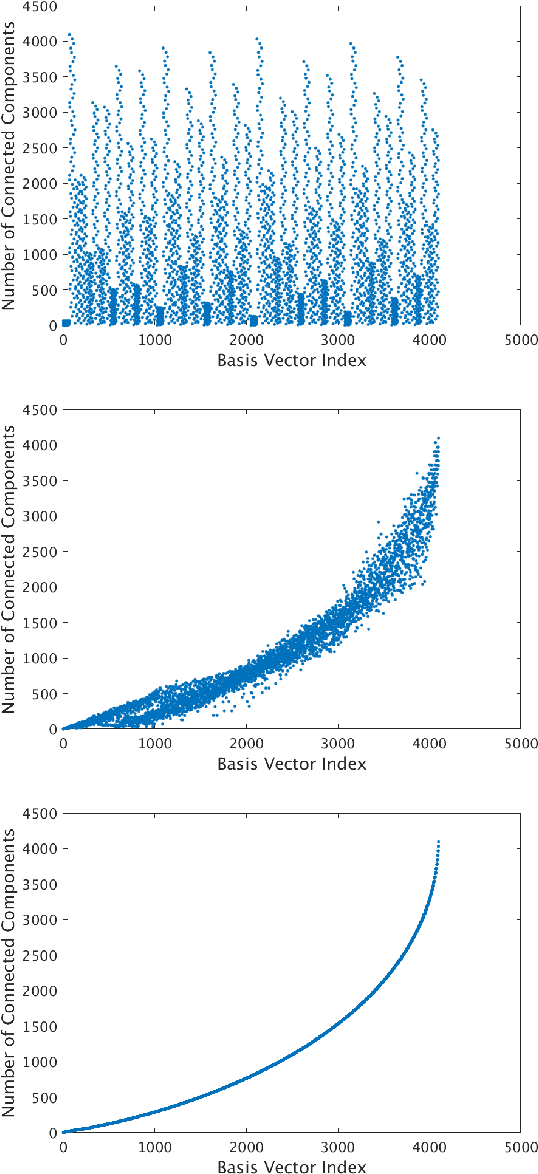
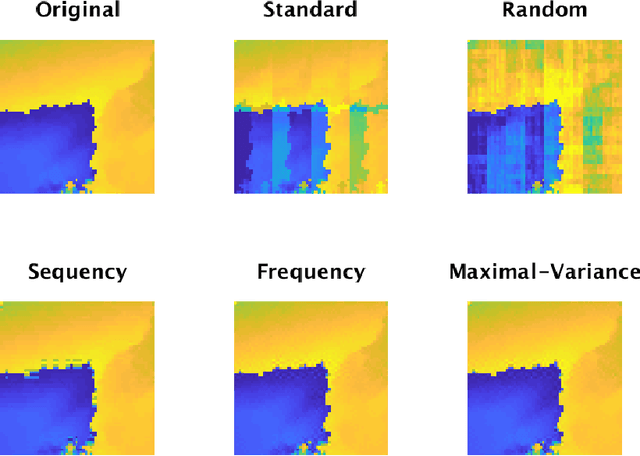
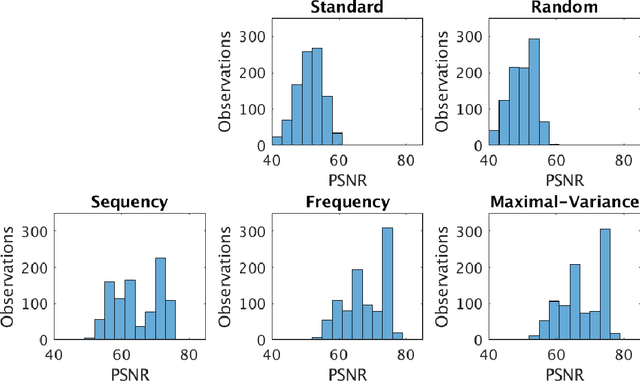
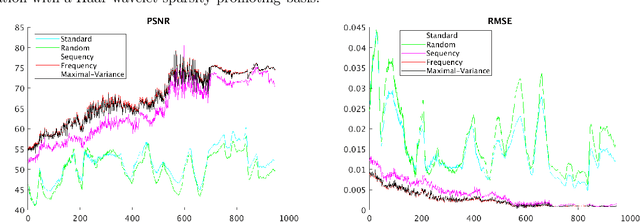
Sampling is a fundamental aspect of any implementation of compressive sensing. Typically, the choice of sampling method is guided by the reconstruction basis. However, this approach can be problematic with respect to certain hardware constraints and is not responsive to domain-specific context. We propose a method for defining an order for a sampling basis that is optimal with respect to capturing variance in data, thus allowing for meaningful sensing at any desired level of compression. We focus on the Walsh-Hadamard sampling basis for its relevance to hardware constraints, but our approach applies to any sampling basis of interest. We illustrate the effectiveness of our method on the Physical Sciences Inc. Fabry-P\'{e}rot interferometer sensor multispectral dataset, the Johns Hopkins Applied Physics Lab FTIR-based longwave infrared sensor hyperspectral dataset, and a Colorado State University Swiss Ranger depth image dataset. The spectral datasets consist of simulant experiments, including releases of chemicals such as GAA and SF6. We combine our sampling and reconstruction with the adaptive coherence estimator (ACE) and bulk coherence for chemical detection and we incorporate an algorithmic threshold for ACE values to determine the presence or absence of a chemical. We compare results across sampling methods in this context. We have successful chemical detection at a compression rate of 90%. For all three datasets, we compare our sampling approach to standard orderings of sampling basis such as random, sequency, and an analog of sequency that we term `frequency.' In one instance, the peak signal to noise ratio was improved by over 30% across a test set of depth images.

Rare geometries: revealing rare categories via dimension-driven statistics

In many situations, the classes of data points of primary interest also happen to be those that are least numerous. A well-known example is detection of fraudulent transactions among the collection of all transactions, the majority of which are legitimate. These types of problems fall under the label of `rare category detection'. One challenging aspect of these problems is that a rare class may not be easily separable from the majority class (at least in terms of available features). Statistics related to the geometry of the rare class (such as its intrinsic dimension) can be significantly different from those for the majority class, reflecting the different dynamics driving variation in the different classes. In this paper we present a new supervised learning algorithm that uses a dimension-driven statistic, called the $\kappa$-profile, to classify unlabeled points as likely to belong to a rare class.

Monitoring the shape of weather, soundscapes, and dynamical systems: a new statistic for dimension-driven data analysis on large data sets

Dimensionality-reduction methods are a fundamental tool in the analysis of large data sets. These algorithms work on the assumption that the "intrinsic dimension" of the data is generally much smaller than the ambient dimension in which it is collected. Alongside their usual purpose of mapping data into a smaller dimension with minimal information loss, dimensionality-reduction techniques implicitly or explicitly provide information about the dimension of the data set. In this paper, we propose a new statistic that we call the $\kappa$-profile for analysis of large data sets. The $\kappa$-profile arises from a dimensionality-reduction optimization problem: namely that of finding a projection into $k$-dimensions that optimally preserves the secants between points in the data set. From this optimal projection we extract $\kappa,$ the norm of the shortest projected secant from among the set of all normalized secants. This $\kappa$ can be computed for any $k$; thus the tuple of $\kappa$ values (indexed by dimension) becomes a $\kappa$-profile. Algorithms such as the Secant-Avoidance Projection algorithm and the Hierarchical Secant-Avoidance Projection algorithm, provide a computationally feasible means of estimating the $\kappa$-profile for large data sets, and thus a method of understanding and monitoring their behavior. As we demonstrate in this paper, the $\kappa$-profile serves as a useful statistic in several representative settings: weather data, soundscape data, and dynamical systems data.

Too many secants: a hierarchical approach to secant-based dimensionality reduction on large data sets

A fundamental question in many data analysis settings is the problem of discerning the "natural" dimension of a data set. That is, when a data set is drawn from a manifold (possibly with noise), a meaningful aspect of the data is the dimension of that manifold. Various approaches exist for estimating this dimension, such as the method of Secant-Avoidance Projection (SAP). Intuitively, the SAP algorithm seeks to determine a projection which best preserves the lengths of all secants between points in a data set; by applying the algorithm to find the best projections to vector spaces of various dimensions, one may infer the dimension of the manifold of origination. That is, one may learn the dimension at which it is possible to construct a diffeomorphic copy of the data in a lower-dimensional Euclidean space. Using Whitney's embedding theorem, we can relate this information to the natural dimension of the data. A drawback of the SAP algorithm is that a data set with $T$ points has $O(T^2)$ secants, making the computation and storage of all secants infeasible for very large data sets. In this paper, we propose a novel algorithm that generalizes the SAP algorithm with an emphasis on addressing this issue. That is, we propose a hierarchical secant-based dimensionality-reduction method, which can be employed for data sets where explicitly calculating all secants is not feasible.

A GPU-Oriented Algorithm Design for Secant-Based Dimensionality Reduction

Dimensionality-reduction techniques are a fundamental tool for extracting useful information from high-dimensional data sets. Because secant sets encode manifold geometry, they are a useful tool for designing meaningful data-reduction algorithms. In one such approach, the goal is to construct a projection that maximally avoids secant directions and hence ensures that distinct data points are not mapped too close together in the reduced space. This type of algorithm is based on a mathematical framework inspired by the constructive proof of Whitney's embedding theorem from differential topology. Computing all (unit) secants for a set of points is by nature computationally expensive, thus opening the door for exploitation of GPU architecture for achieving fast versions of these algorithms. We present a polynomial-time data-reduction algorithm that produces a meaningful low-dimensional representation of a data set by iteratively constructing improved projections within the framework described above. Key to our algorithm design and implementation is the use of GPUs which, among other things, minimizes the computational time required for the calculation of all secant lines. One goal of this report is to share ideas with GPU experts and to discuss a class of mathematical algorithms that may be of interest to the broader GPU community.

Endmember Extraction on the Grassmannian

Endmember extraction plays a prominent role in a variety of data analysis problems as endmembers often correspond to data representing the purest or best representative of some feature. Identifying endmembers then can be useful for further identification and classification tasks. In settings with high-dimensional data, such as hyperspectral imagery, it can be useful to consider endmembers that are subspaces as they are capable of capturing a wider range of variations of a signature. The endmember extraction problem in this setting thus translates to finding the vertices of the convex hull of a set of points on a Grassmannian. In the presence of noise, it can be less clear whether a point should be considered a vertex. In this paper, we propose an algorithm to extract endmembers on a Grassmannian, identify subspaces of interest that lie near the boundary of a convex hull, and demonstrate the use of the algorithm on a synthetic example and on the 220 spectral band AVIRIS Indian Pines hyperspectral image.