A data-driven approach to sampling matrix selection for compressive sensing
Paper and Code
Jun 20, 2019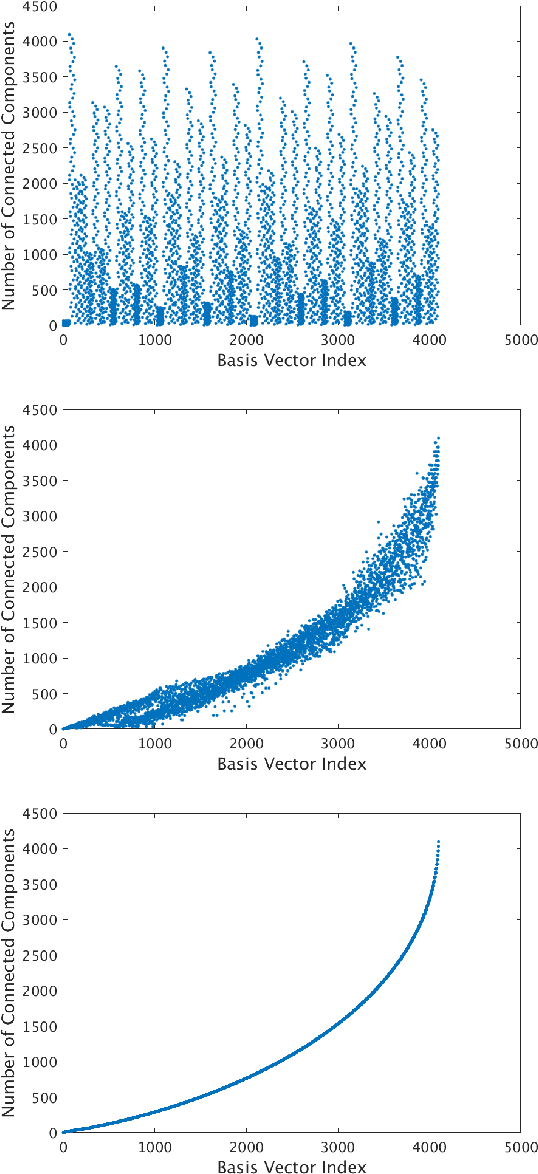
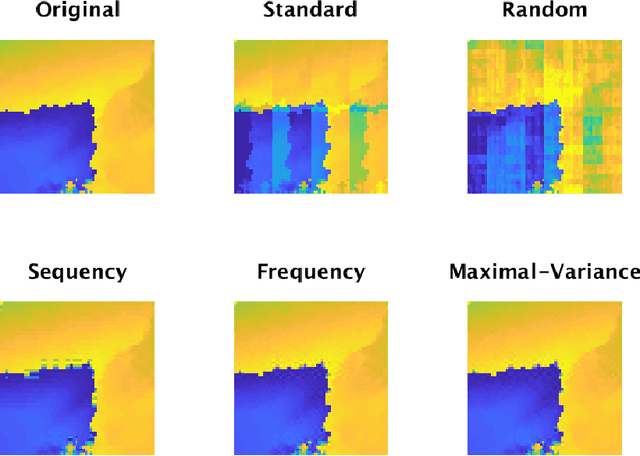
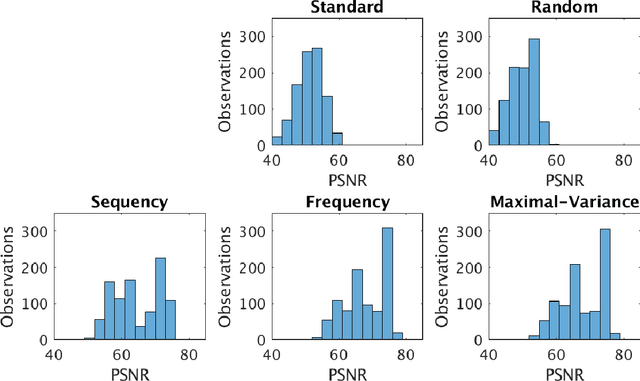
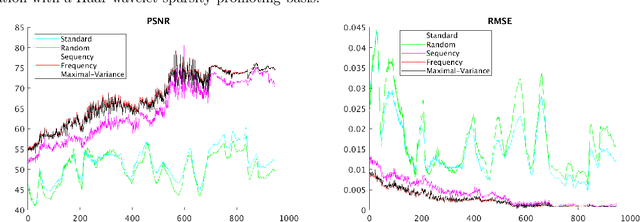
Sampling is a fundamental aspect of any implementation of compressive sensing. Typically, the choice of sampling method is guided by the reconstruction basis. However, this approach can be problematic with respect to certain hardware constraints and is not responsive to domain-specific context. We propose a method for defining an order for a sampling basis that is optimal with respect to capturing variance in data, thus allowing for meaningful sensing at any desired level of compression. We focus on the Walsh-Hadamard sampling basis for its relevance to hardware constraints, but our approach applies to any sampling basis of interest. We illustrate the effectiveness of our method on the Physical Sciences Inc. Fabry-P\'{e}rot interferometer sensor multispectral dataset, the Johns Hopkins Applied Physics Lab FTIR-based longwave infrared sensor hyperspectral dataset, and a Colorado State University Swiss Ranger depth image dataset. The spectral datasets consist of simulant experiments, including releases of chemicals such as GAA and SF6. We combine our sampling and reconstruction with the adaptive coherence estimator (ACE) and bulk coherence for chemical detection and we incorporate an algorithmic threshold for ACE values to determine the presence or absence of a chemical. We compare results across sampling methods in this context. We have successful chemical detection at a compression rate of 90%. For all three datasets, we compare our sampling approach to standard orderings of sampling basis such as random, sequency, and an analog of sequency that we term `frequency.' In one instance, the peak signal to noise ratio was improved by over 30% across a test set of depth images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge