Dual Graphs of Polyhedral Decompositions for the Detection of Adversarial Attacks

Previous work has shown that a neural network with the rectified linear unit (ReLU) activation function leads to a convex polyhedral decomposition of the input space. These decompositions can be represented by a dual graph with vertices corresponding to polyhedra and edges corresponding to polyhedra sharing a facet, which is a subgraph of a Hamming graph. This paper illustrates how one can utilize the dual graph to detect and analyze adversarial attacks in the context of digital images. When an image passes through a network containing ReLU nodes, the firing or non-firing at a node can be encoded as a bit ($1$ for ReLU activation, $0$ for ReLU non-activation). The sequence of all bit activations identifies the image with a bit vector, which identifies it with a polyhedron in the decomposition and, in turn, identifies it with a vertex in the dual graph. We identify ReLU bits that are discriminators between non-adversarial and adversarial images and examine how well collections of these discriminators can ensemble vote to build an adversarial image detector. Specifically, we examine the similarities and differences of ReLU bit vectors for adversarial images, and their non-adversarial counterparts, using a pre-trained ResNet-50 architecture. While this paper focuses on adversarial digital images, ResNet-50 architecture, and the ReLU activation function, our methods extend to other network architectures, activation functions, and types of datasets.

A Primer on Topological Data Analysis to Support Image Analysis Tasks in Environmental Science

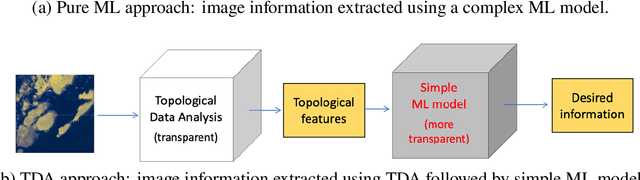
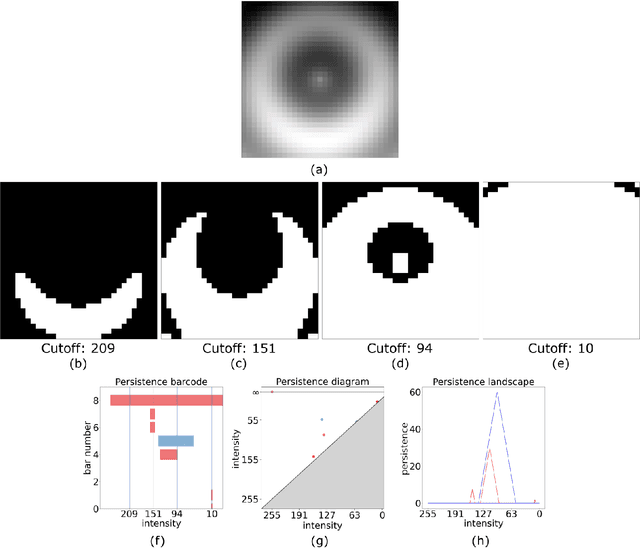
Topological data analysis (TDA) is a tool from data science and mathematics that is beginning to make waves in environmental science. In this work, we seek to provide an intuitive and understandable introduction to a tool from TDA that is particularly useful for the analysis of imagery, namely persistent homology. We briefly discuss the theoretical background but focus primarily on understanding the output of this tool and discussing what information it can glean. To this end, we frame our discussion around a guiding example of classifying satellite images from the Sugar, Fish, Flower, and Gravel Dataset produced for the study of mesocale organization of clouds by Rasp et. al. in 2020 (arXiv:1906:01906). We demonstrate how persistent homology and its vectorization, persistence landscapes, can be used in a workflow with a simple machine learning algorithm to obtain good results, and explore in detail how we can explain this behavior in terms of image-level features. One of the core strengths of persistent homology is how interpretable it can be, so throughout this paper we discuss not just the patterns we find, but why those results are to be expected given what we know about the theory of persistent homology. Our goal is that a reader of this paper will leave with a better understanding of TDA and persistent homology, be able to identify problems and datasets of their own for which persistent homology could be helpful, and gain an understanding of results they obtain from applying the included GitHub example code.

Formulating Beurling LASSO for Source Separation via Proximal Gradient Iteration

Beurling LASSO generalizes the LASSO problem to finite Radon measures regularized via their total variation. Despite its theoretical appeal, this space is hard to parametrize, which poses an algorithmic challenge. We propose a formulation of continuous convolutional source separation with Beurling LASSO that avoids the explicit computation of the measures and instead employs the duality transform of the proximal mapping.

Blind Source Separation in Polyphonic Music Recordings Using Deep Neural Networks Trained via Policy Gradients

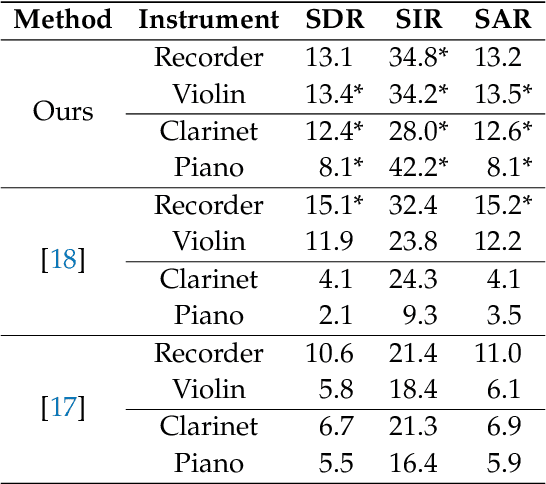
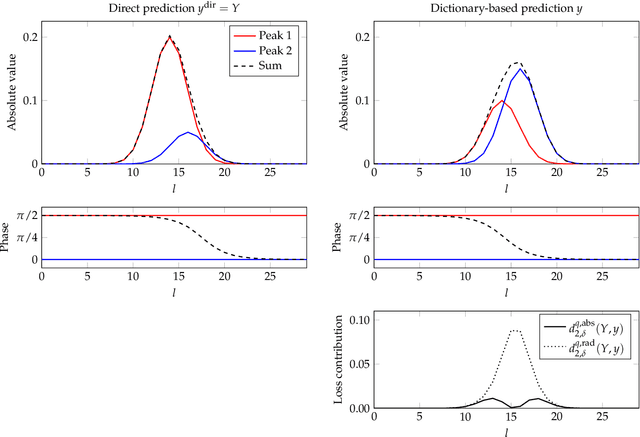
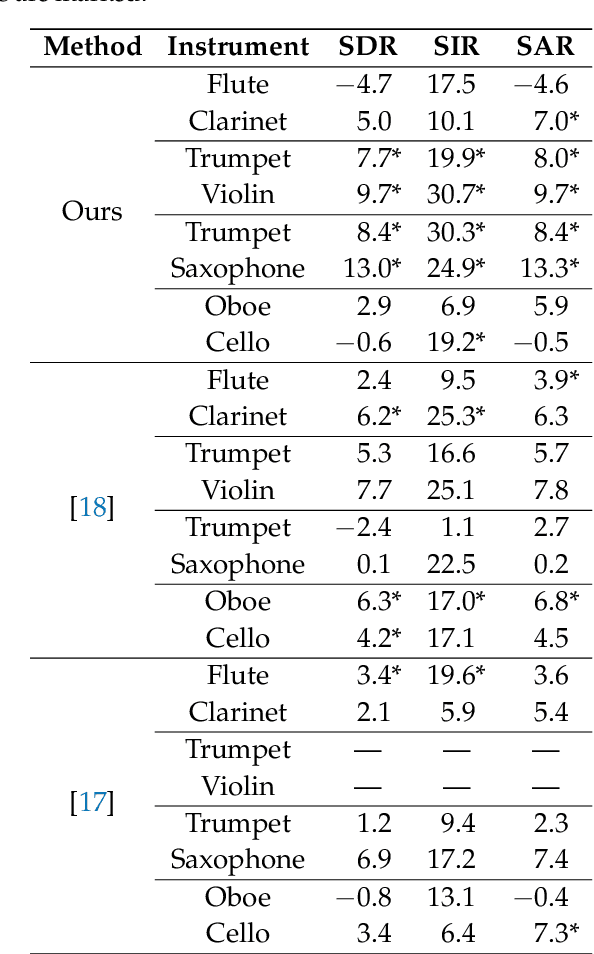
We propose a method for the blind separation of sounds of musical instruments in audio signals. We describe the individual tones via a parametric model, training a dictionary to capture the relative amplitudes of the harmonics. The model parameters are predicted via a U-Net, which is a type of deep neural network. The network is trained without ground truth information, based on the difference between the model prediction and the individual time frames of the short-time Fourier transform. Since some of the model parameters do not yield a useful backpropagation gradient, we model them stochastically and employ the policy gradient instead. To provide phase information and account for inaccuracies in the dictionary-based representation, we also let the network output a direct prediction, which we then use to resynthesize the audio signals for the individual instruments. Due to the flexibility of the neural network, inharmonicity can be incorporated seamlessly and no preprocessing of the input spectra is required. Our algorithm yields high-quality separation results with particularly low interference on a variety of different audio samples, both acoustic and synthetic, provided that the sample contains enough data for the training and that the spectral characteristics of the musical instruments are sufficiently stable to be approximated by the dictionary.

Edge, Ridge, and Blob Detection with Symmetric Molecules

We present a novel approach to the detection and characterization of edges, ridges, and blobs in two-dimensional images which exploits the symmetry properties of directionally sensitive analyzing functions in multiscale systems that are constructed in the framework of alpha-molecules. The proposed feature detectors are inspired by the notion of phase congruency, stable in the presence of noise, and by definition invariant to changes in contrast. We also show how the behavior of coefficients corresponding to differently scaled and oriented analyzing functions can be used to obtain a comprehensive characterization of the geometry of features in terms of local tangent directions, widths, and heights. The accuracy and robustness of the proposed measures are validated and compared to various state-of-the-art algorithms in extensive numerical experiments in which we consider sets of clean and distorted synthetic images that are associated with reliable ground truths. To further demonstrate the applicability, we show how the proposed ridge measure can be used to detect and characterize blood vessels in digital retinal images and how the proposed blob measure can be applied to automatically count the number of cell colonies in a Petri dish.

Singular Values for ReLU Layers

Despite their prevalence in neural networks we still lack a thorough theoretical characterization of ReLU layers. This paper aims to further our understanding of ReLU layers by studying how the activation function ReLU interacts with the linear component of the layer and what role this interaction plays in the success of the neural network in achieving its intended task. To this end, we introduce two new tools: ReLU singular values of operators and the Gaussian mean width of operators. By presenting on the one hand theoretical justifications, results, and interpretations of these two concepts and on the other hand numerical experiments and results of the ReLU singular values and the Gaussian mean width being applied to trained neural networks, we hope to give a comprehensive, singular-value-centric view of ReLU layers. We find that ReLU singular values and the Gaussian mean width do not only enable theoretical insights, but also provide one with metrics which seem promising for practical applications. In particular, these measures can be used to distinguish correctly and incorrectly classified data as it traverses the network. We conclude by introducing two tools based on our findings: double-layers and harmonic pruning.

Musical Instrument Separation on Shift-Invariant Spectrograms via Stochastic Dictionary Learning

We propose a novel method for the blind separation of audio signals produced by musical instruments. While the approach of applying non-negative matrix factorization (NMF) has been studied in many papers, it does not make use of the pitch-invariance that the sounds of instruments exhibit. This limitation can be overcome by using tensor factorization, in which context the use of log-frequency spectrograms was initiated, but this still requires the specific tuning of the instruments to be hard-coded into the algorithm. We develop a time-frequency representation that is both shift-invariant and frequency-aligned, with a variant that can also be used for wideband signals. Our separation algorithm exploits this shift-invariance in order to find patterns of peaks related to specific instruments, while non-linear optimization enables it to represent arbitrary frequencies and incorporate inharmonicity, and the reasonability of the representation is ensured by a sparsity condition. The relative amplitudes of the harmonics are saved in a dictionary, which is trained via a modified version of ADAM. For a realistic monaural piece with acoustic recorder and violin, we achieve qualitatively good separation with a signal-to-distortion ratio (SDR) of 12.5 dB, a signal-to-interference ratio (SIR) of 25.7 dB, and a signal-to-artifacts ratio (SAR) of 12.7 dB, averaged.

Shearlet-Based Detection of Flame Fronts

Identifying and characterizing flame fronts is the most common task in the computer-assisted analysis of data obtained from imaging techniques such as planar laser-induced fluorescence (PLIF), laser Rayleigh scattering (LRS), or particle imaging velocimetry (PIV). We present a novel edge and ridge (line) detection algorithm based on complex-valued wavelet-like analyzing functions -- so-called complex shearlets -- displaying several traits useful for the extraction of flame fronts. In addition to providing a unified approach to the detection of edges and ridges, our method inherently yields estimates of local tangent orientations and local curvatures. To examine the applicability for high-frequency recordings of combustion processes, the algorithm is applied to mock images distorted with varying degrees of noise and real-world PLIF images of both OH and CH radicals. Furthermore, we compare the performance of the newly proposed complex shearlet-based measure to well-established edge and ridge detection techniques such as the Canny edge detector, another shearlet-based edge detector, and the phase congruency measure.