Formulating Beurling LASSO for Source Separation via Proximal Gradient Iteration

Beurling LASSO generalizes the LASSO problem to finite Radon measures regularized via their total variation. Despite its theoretical appeal, this space is hard to parametrize, which poses an algorithmic challenge. We propose a formulation of continuous convolutional source separation with Beurling LASSO that avoids the explicit computation of the measures and instead employs the duality transform of the proximal mapping.

Blind Source Separation in Polyphonic Music Recordings Using Deep Neural Networks Trained via Policy Gradients

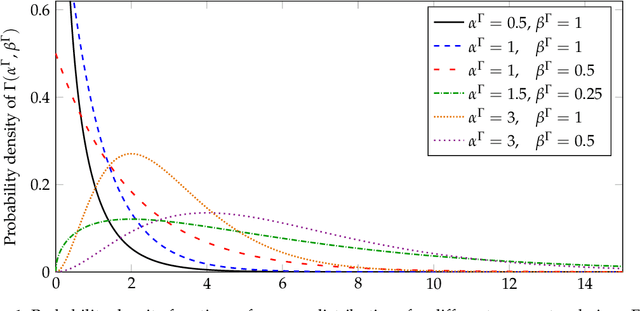
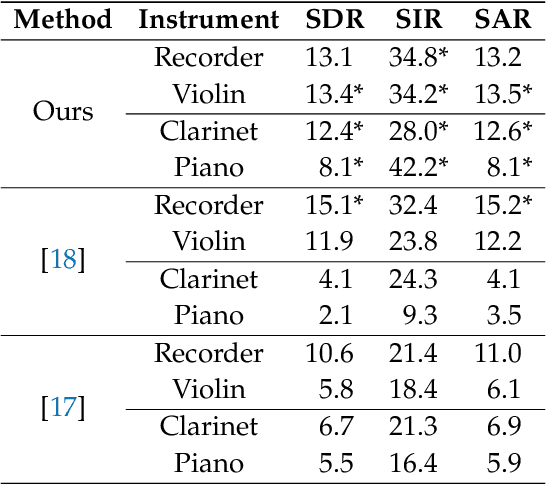
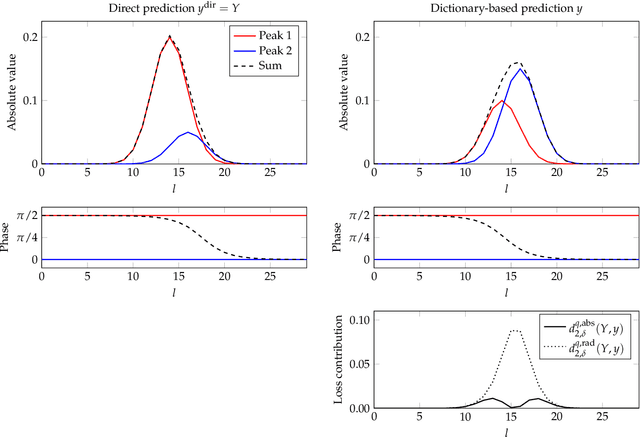
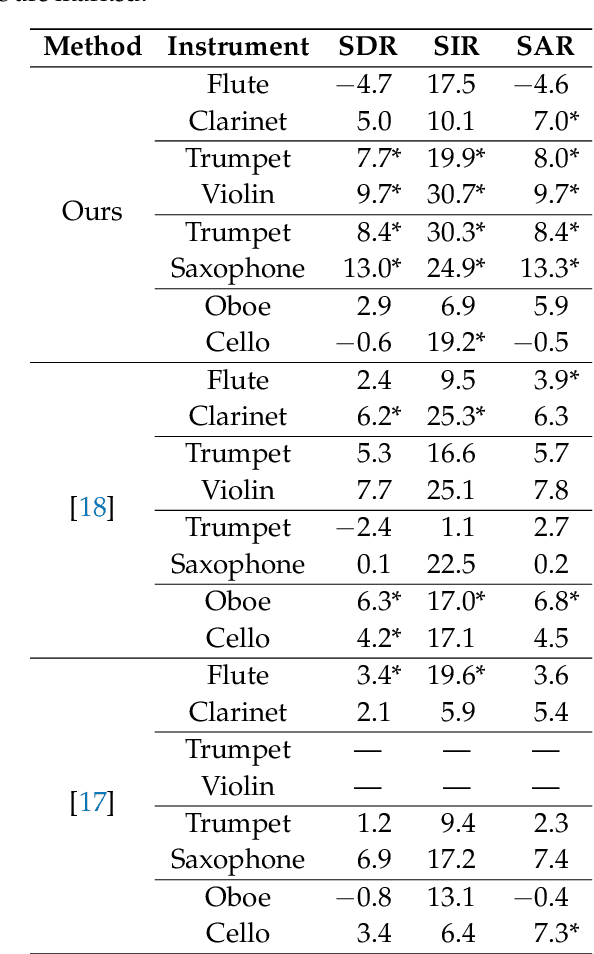
We propose a method for the blind separation of sounds of musical instruments in audio signals. We describe the individual tones via a parametric model, training a dictionary to capture the relative amplitudes of the harmonics. The model parameters are predicted via a U-Net, which is a type of deep neural network. The network is trained without ground truth information, based on the difference between the model prediction and the individual time frames of the short-time Fourier transform. Since some of the model parameters do not yield a useful backpropagation gradient, we model them stochastically and employ the policy gradient instead. To provide phase information and account for inaccuracies in the dictionary-based representation, we also let the network output a direct prediction, which we then use to resynthesize the audio signals for the individual instruments. Due to the flexibility of the neural network, inharmonicity can be incorporated seamlessly and no preprocessing of the input spectra is required. Our algorithm yields high-quality separation results with particularly low interference on a variety of different audio samples, both acoustic and synthetic, provided that the sample contains enough data for the training and that the spectral characteristics of the musical instruments are sufficiently stable to be approximated by the dictionary.

Musical Instrument Separation on Shift-Invariant Spectrograms via Stochastic Dictionary Learning

We propose a novel method for the blind separation of audio signals produced by musical instruments. While the approach of applying non-negative matrix factorization (NMF) has been studied in many papers, it does not make use of the pitch-invariance that the sounds of instruments exhibit. This limitation can be overcome by using tensor factorization, in which context the use of log-frequency spectrograms was initiated, but this still requires the specific tuning of the instruments to be hard-coded into the algorithm. We develop a time-frequency representation that is both shift-invariant and frequency-aligned, with a variant that can also be used for wideband signals. Our separation algorithm exploits this shift-invariance in order to find patterns of peaks related to specific instruments, while non-linear optimization enables it to represent arbitrary frequencies and incorporate inharmonicity, and the reasonability of the representation is ensured by a sparsity condition. The relative amplitudes of the harmonics are saved in a dictionary, which is trained via a modified version of ADAM. For a realistic monaural piece with acoustic recorder and violin, we achieve qualitatively good separation with a signal-to-distortion ratio (SDR) of 12.5 dB, a signal-to-interference ratio (SIR) of 25.7 dB, and a signal-to-artifacts ratio (SAR) of 12.7 dB, averaged.