Minimal Cycle Representatives in Persistent Homology using Linear Programming: an Empirical Study with User's Guide

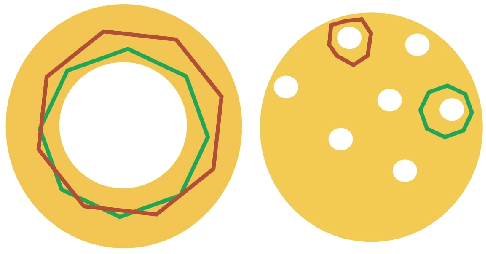
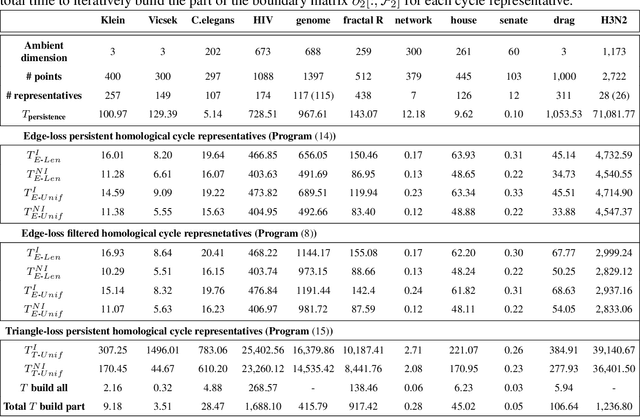
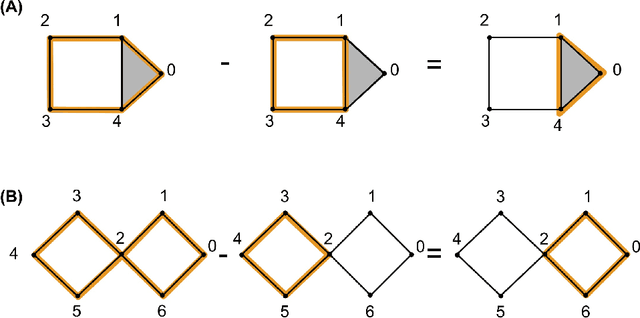
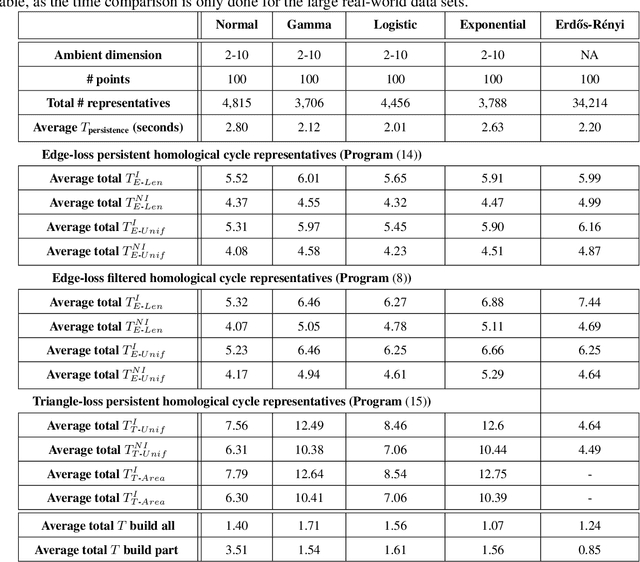
Cycle representatives of persistent homology classes can be used to provide descriptions of topological features in data. However, the non-uniqueness of these representatives creates ambiguity and can lead to many different interpretations of the same set of classes. One approach to solving this problem is to optimize the choice of representative against some measure that is meaningful in the context of the data. In this work, we provide a study of the effectiveness and computational cost of several $\ell_1$-minimization optimization procedures for constructing homological cycle bases for persistent homology with rational coefficients in dimension one, including uniform-weighted and length-weighted edge-loss algorithms as well as uniform-weighted and area-weighted triangle-loss algorithms. We conduct these optimizations via standard linear programming methods, applying general-purpose solvers to optimize over column bases of simplicial boundary matrices. Our key findings are: (i) optimization is effective in reducing the size of cycle representatives, (ii) the computational cost of optimizing a basis of cycle representatives exceeds the cost of computing such a basis in most data sets we consider, (iii) the choice of linear solvers matters a lot to the computation time of optimizing cycles, (iv) the computation time of solving an integer program is not significantly longer than the computation time of solving a linear program for most of the cycle representatives, using the Gurobi linear solver, (v) strikingly, whether requiring integer solutions or not, we almost always obtain a solution with the same cost and almost all solutions found have entries in {-1, 0, 1} and therefore, are also solutions to a restricted $\ell_0$ optimization problem, and (vi) we obtain qualitatively different results for generators in Erd\H{o}s-R\'enyi random clique complexes.

Capturing Dynamics of Time-Varying Data via Topology

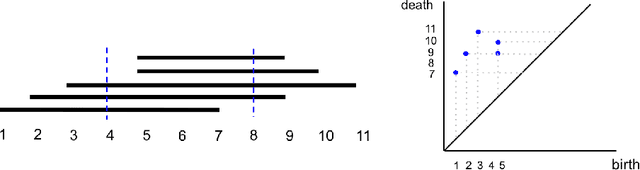
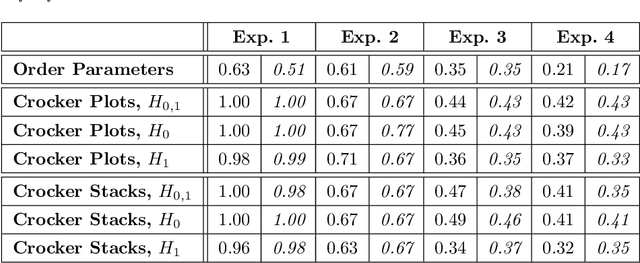
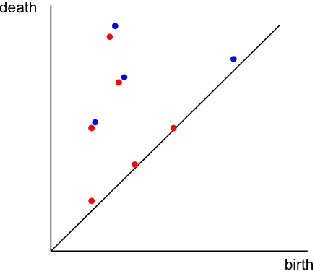
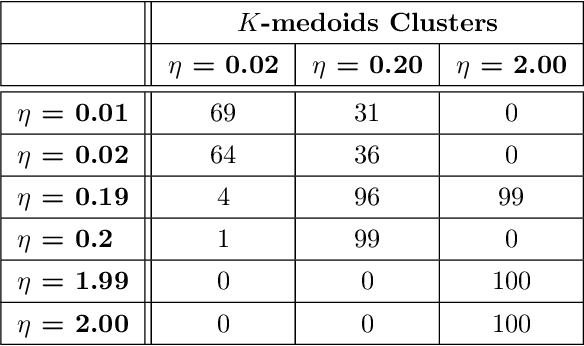
One approach to understanding complex data is to study its shape through the lens of algebraic topology. While the early development of topological data analysis focused primarily on static data, in recent years, theoretical and applied studies have turned to data that varies in time. A time-varying collection of metric spaces as formed, for example, by a moving school of fish or flock of birds, can contain a vast amount of information. There is often a need to simplify or summarize the dynamic behavior. We provide an introduction to topological summaries of time-varying metric spaces including vineyards [17], crocker plots [52], and multiparameter rank functions [34]. We then introduce a new tool to summarize time-varying metric spaces: a crocker stack. Crocker stacks are convenient for visualization, amenable to machine learning, and satisfy a desirable stability property which we prove. We demonstrate the utility of crocker stacks for a parameter identification task involving an influential model of biological aggregations [54]. Altogether, we aim to bring the broader applied mathematics community up-to-date on topological summaries of time-varying metric spaces.

Persistence Images: A Stable Vector Representation of Persistent Homology

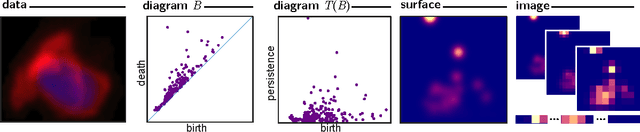
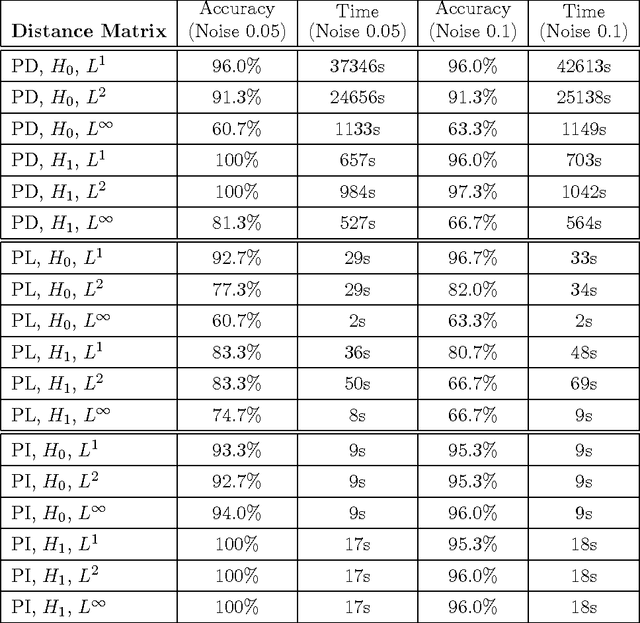
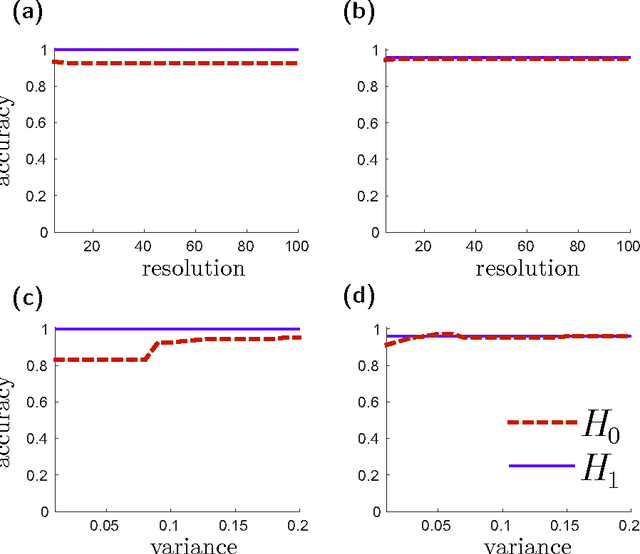
Many datasets can be viewed as a noisy sampling of an underlying space, and tools from topological data analysis can characterize this structure for the purpose of knowledge discovery. One such tool is persistent homology, which provides a multiscale description of the homological features within a dataset. A useful representation of this homological information is a persistence diagram (PD). Efforts have been made to map PDs into spaces with additional structure valuable to machine learning tasks. We convert a PD to a finite-dimensional vector representation which we call a persistence image (PI), and prove the stability of this transformation with respect to small perturbations in the inputs. The discriminatory power of PIs is compared against existing methods, showing significant performance gains. We explore the use of PIs with vector-based machine learning tools, such as linear sparse support vector machines, which identify features containing discriminating topological information. Finally, high accuracy inference of parameter values from the dynamic output of a discrete dynamical system (the linked twist map) and a partial differential equation (the anisotropic Kuramoto-Sivashinsky equation) provide a novel application of the discriminatory power of PIs.

Persistent Homology on Grassmann Manifolds for Analysis of Hyperspectral Movies

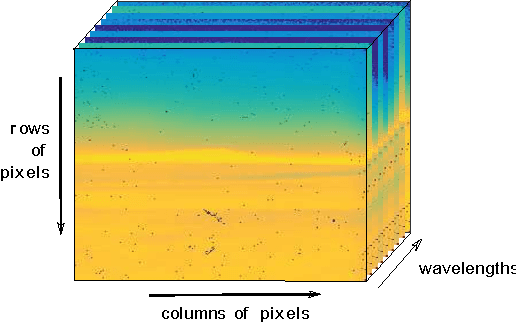
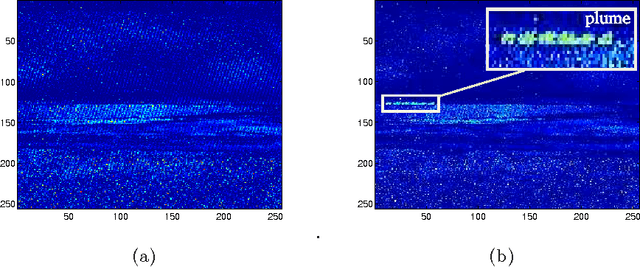
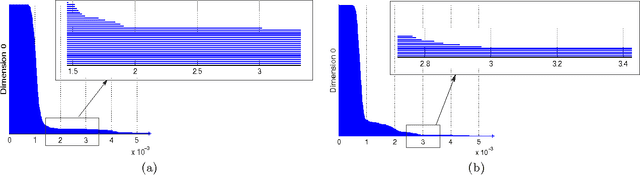
The existence of characteristic structure, or shape, in complex data sets has been recognized as increasingly important for mathematical data analysis. This realization has motivated the development of new tools such as persistent homology for exploring topological invariants, or features, in large data sets. In this paper we apply persistent homology to the characterization of gas plumes in time dependent sequences of hyperspectral cubes, i.e. the analysis of 4-way arrays. We investigate hyperspectral movies of Long-Wavelength Infrared data monitoring an experimental release of chemical simulant into the air. Our approach models regions of interest within the hyperspectral data cubes as points on the real Grassmann manifold $G(k, n)$ (whose points parameterize the $k$-dimensional subspaces of $\mathbb{R}^n$), contrasting our approach with the more standard framework in Euclidean space. An advantage of this approach is that it allows a sequence of time slices in a hyperspectral movie to be collapsed to a sequence of points in such a way that some of the key structure within and between the slices is encoded by the points on the Grassmann manifold. This motivates the search for topological features, associated with the evolution of the frames of a hyperspectral movie, within the corresponding points on the Grassmann manifold. The proposed mathematical model affords the processing of large data sets while retaining valuable discriminatory information. In this paper, we discuss how embedding our data in the Grassmann manifold, together with topological data analysis, captures dynamical events that occur as the chemical plume is released and evolves.

Locally Linear Embedding Clustering Algorithm for Natural Imagery

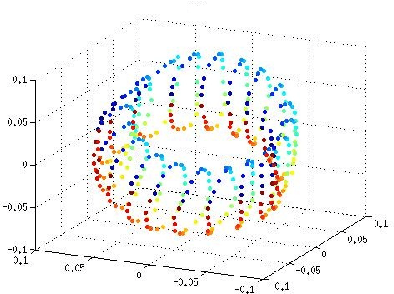
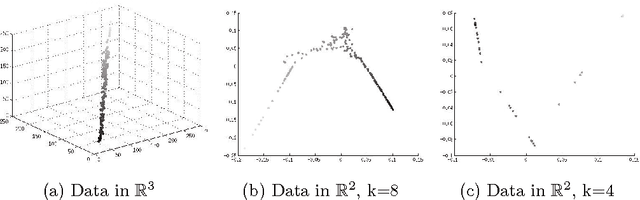
The ability to characterize the color content of natural imagery is an important application of image processing. The pixel by pixel coloring of images may be viewed naturally as points in color space, and the inherent structure and distribution of these points affords a quantization, through clustering, of the color information in the image. In this paper, we present a novel topologically driven clustering algorithm that permits segmentation of the color features in a digital image. The algorithm blends Locally Linear Embedding (LLE) and vector quantization by mapping color information to a lower dimensional space, identifying distinct color regions, and classifying pixels together based on both a proximity measure and color content. It is observed that these techniques permit a significant reduction in color resolution while maintaining the visually important features of images.