Persistence Images: A Stable Vector Representation of Persistent Homology

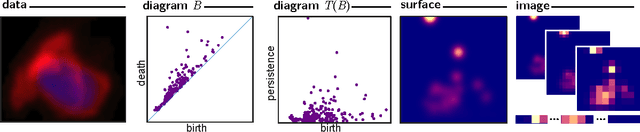
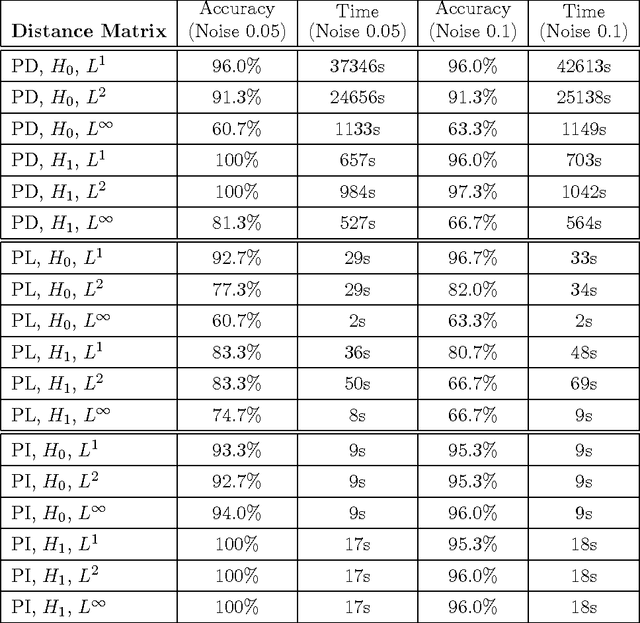
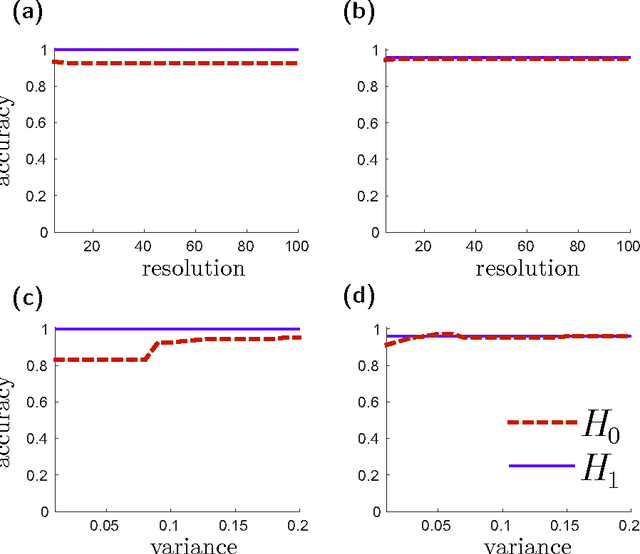
Many datasets can be viewed as a noisy sampling of an underlying space, and tools from topological data analysis can characterize this structure for the purpose of knowledge discovery. One such tool is persistent homology, which provides a multiscale description of the homological features within a dataset. A useful representation of this homological information is a persistence diagram (PD). Efforts have been made to map PDs into spaces with additional structure valuable to machine learning tasks. We convert a PD to a finite-dimensional vector representation which we call a persistence image (PI), and prove the stability of this transformation with respect to small perturbations in the inputs. The discriminatory power of PIs is compared against existing methods, showing significant performance gains. We explore the use of PIs with vector-based machine learning tools, such as linear sparse support vector machines, which identify features containing discriminating topological information. Finally, high accuracy inference of parameter values from the dynamic output of a discrete dynamical system (the linked twist map) and a partial differential equation (the anisotropic Kuramoto-Sivashinsky equation) provide a novel application of the discriminatory power of PIs.

Persistent Homology on Grassmann Manifolds for Analysis of Hyperspectral Movies

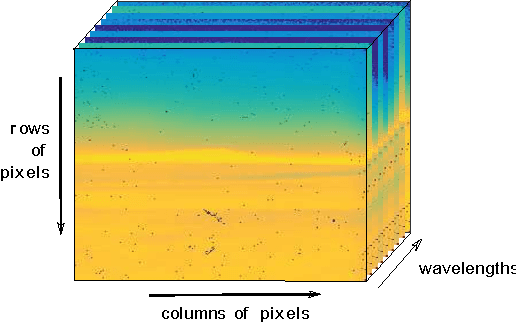
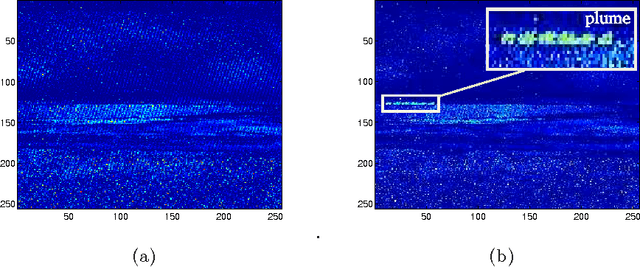
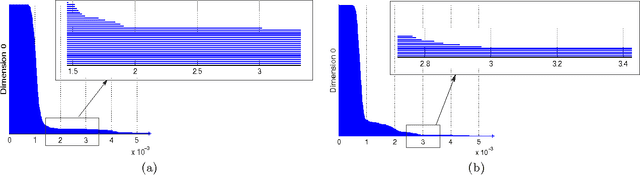
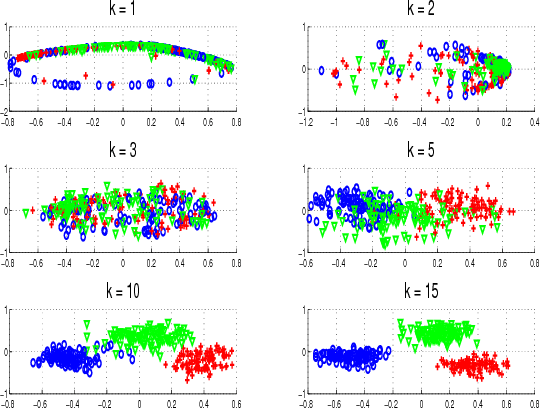
The existence of characteristic structure, or shape, in complex data sets has been recognized as increasingly important for mathematical data analysis. This realization has motivated the development of new tools such as persistent homology for exploring topological invariants, or features, in large data sets. In this paper we apply persistent homology to the characterization of gas plumes in time dependent sequences of hyperspectral cubes, i.e. the analysis of 4-way arrays. We investigate hyperspectral movies of Long-Wavelength Infrared data monitoring an experimental release of chemical simulant into the air. Our approach models regions of interest within the hyperspectral data cubes as points on the real Grassmann manifold $G(k, n)$ (whose points parameterize the $k$-dimensional subspaces of $\mathbb{R}^n$), contrasting our approach with the more standard framework in Euclidean space. An advantage of this approach is that it allows a sequence of time slices in a hyperspectral movie to be collapsed to a sequence of points in such a way that some of the key structure within and between the slices is encoded by the points on the Grassmann manifold. This motivates the search for topological features, associated with the evolution of the frames of a hyperspectral movie, within the corresponding points on the Grassmann manifold. The proposed mathematical model affords the processing of large data sets while retaining valuable discriminatory information. In this paper, we discuss how embedding our data in the Grassmann manifold, together with topological data analysis, captures dynamical events that occur as the chemical plume is released and evolves.

Classification of Hyperspectral Imagery on Embedded Grassmannians

We propose an approach for capturing the signal variability in hyperspectral imagery using the framework of the Grassmann manifold. Labeled points from each class are sampled and used to form abstract points on the Grassmannian. The resulting points on the Grassmannian have representations as orthonormal matrices and as such do not reside in Euclidean space in the usual sense. There are a variety of metrics which allow us to determine a distance matrices that can be used to realize the Grassmannian as an embedding in Euclidean space. We illustrate that we can achieve an approximately isometric embedding of the Grassmann manifold using the chordal metric while this is not the case with geodesic distances. However, non-isometric embeddings generated by using a pseudometric on the Grassmannian lead to the best classification results. We observe that as the dimension of the Grassmannian grows, the accuracy of the classification grows to 100% on two illustrative examples. We also observe a decrease in classification rates if the dimension of the points on the Grassmannian is too large for the dimension of the Euclidean space. We use sparse support vector machines to perform additional model reduction. The resulting classifier selects a subset of dimensions of the embedding without loss in classification performance.