Classification of Hyperspectral Imagery on Embedded Grassmannians
Paper and Code
Feb 03, 2015

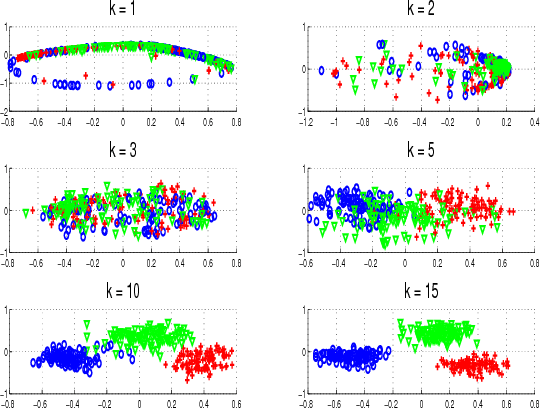

We propose an approach for capturing the signal variability in hyperspectral imagery using the framework of the Grassmann manifold. Labeled points from each class are sampled and used to form abstract points on the Grassmannian. The resulting points on the Grassmannian have representations as orthonormal matrices and as such do not reside in Euclidean space in the usual sense. There are a variety of metrics which allow us to determine a distance matrices that can be used to realize the Grassmannian as an embedding in Euclidean space. We illustrate that we can achieve an approximately isometric embedding of the Grassmann manifold using the chordal metric while this is not the case with geodesic distances. However, non-isometric embeddings generated by using a pseudometric on the Grassmannian lead to the best classification results. We observe that as the dimension of the Grassmannian grows, the accuracy of the classification grows to 100% on two illustrative examples. We also observe a decrease in classification rates if the dimension of the points on the Grassmannian is too large for the dimension of the Euclidean space. We use sparse support vector machines to perform additional model reduction. The resulting classifier selects a subset of dimensions of the embedding without loss in classification performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge