STARS: Sensor-agnostic Transformer Architecture for Remote Sensing

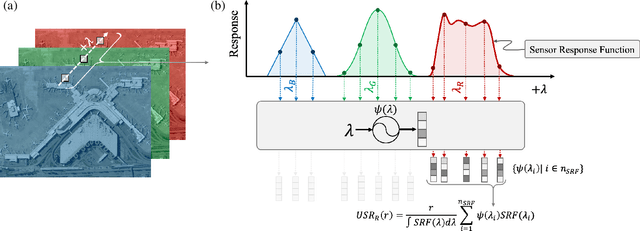
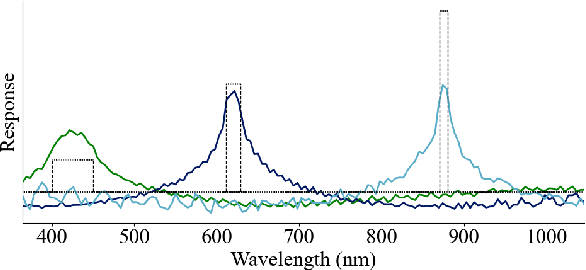
We present a sensor-agnostic spectral transformer as the basis for spectral foundation models. To that end, we introduce a Universal Spectral Representation (USR) that leverages sensor meta-data, such as sensing kernel specifications and sensing wavelengths, to encode spectra obtained from any spectral instrument into a common representation, such that a single model can ingest data from any sensor. Furthermore, we develop a methodology for pre-training such models in a self-supervised manner using a novel random sensor-augmentation and reconstruction pipeline to learn spectral features independent of the sensing paradigm. We demonstrate that our architecture can learn sensor independent spectral features that generalize effectively to sensors not seen during training. This work sets the stage for training foundation models that can both leverage and be effective for the growing diversity of spectral data.

ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

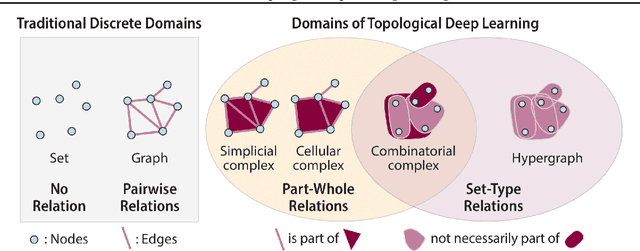
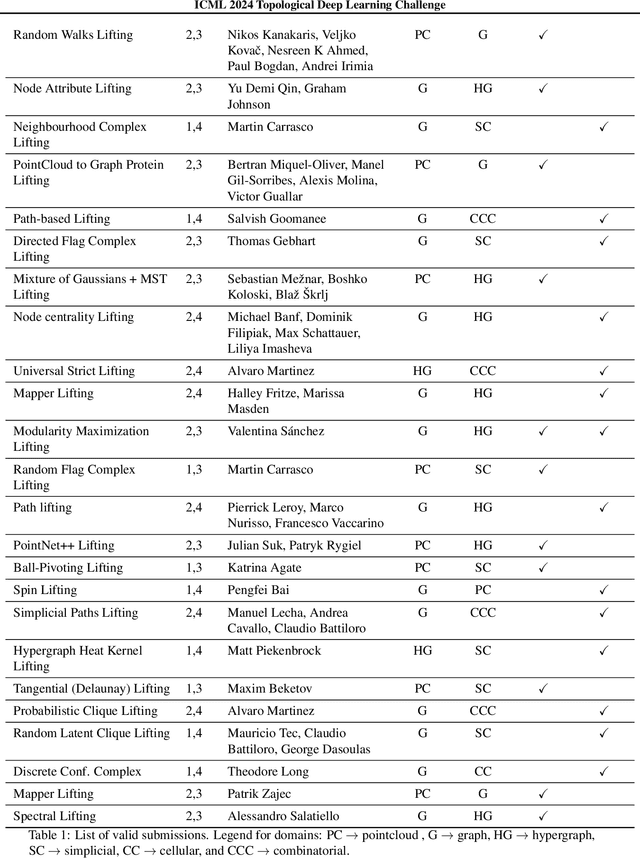
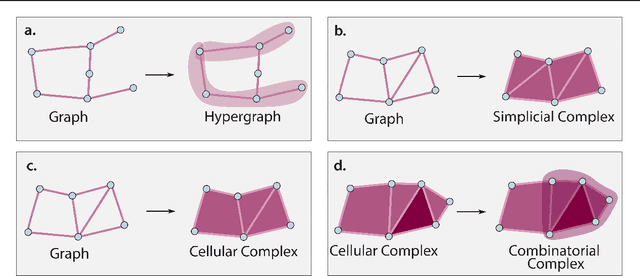
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

Generalist Multimodal AI: A Review of Architectures, Challenges and Opportunities

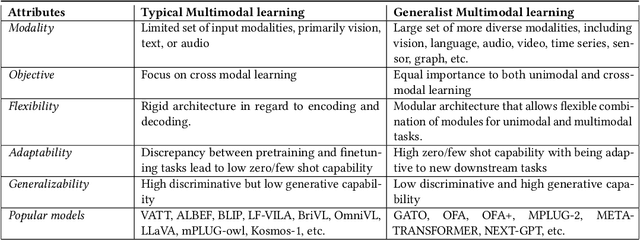
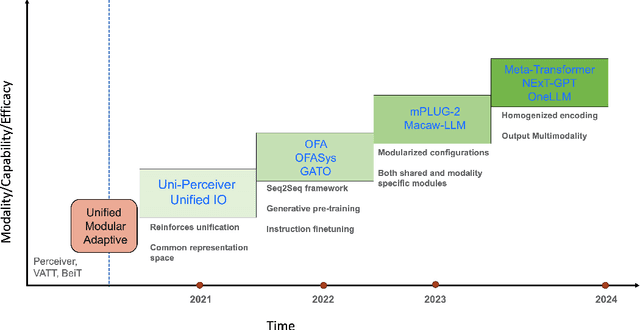
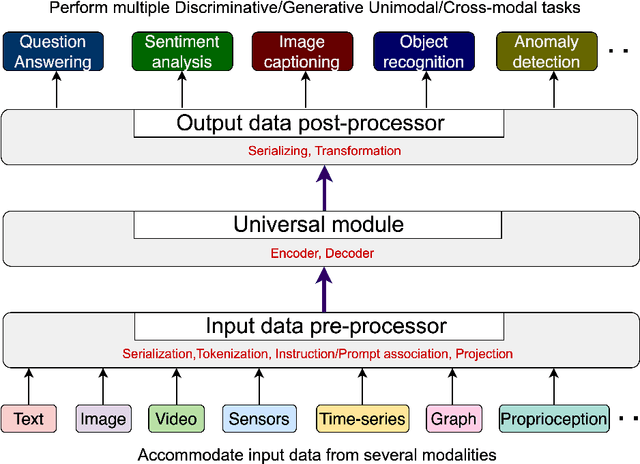
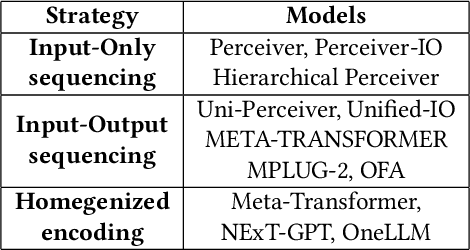
Multimodal models are expected to be a critical component to future advances in artificial intelligence. This field is starting to grow rapidly with a surge of new design elements motivated by the success of foundation models in natural language processing (NLP) and vision. It is widely hoped that further extending the foundation models to multiple modalities (e.g., text, image, video, sensor, time series, graph, etc.) will ultimately lead to generalist multimodal models, i.e. one model across different data modalities and tasks. However, there is little research that systematically analyzes recent multimodal models (particularly the ones that work beyond text and vision) with respect to the underling architecture proposed. Therefore, this work provides a fresh perspective on generalist multimodal models (GMMs) via a novel architecture and training configuration specific taxonomy. This includes factors such as Unifiability, Modularity, and Adaptability that are pertinent and essential to the wide adoption and application of GMMs. The review further highlights key challenges and prospects for the field and guide the researchers into the new advancements.

Data-Driven Invertible Neural Surrogates of Atmospheric Transmission

We present a framework for inferring an atmospheric transmission profile from a spectral scene. This framework leverages a lightweight, physics-based simulator that is automatically tuned - by virtue of autodifferentiation and differentiable programming - to construct a surrogate atmospheric profile to model the observed data. We demonstrate utility of the methodology by (i) performing atmospheric correction, (ii) recasting spectral data between various modalities (e.g. radiance and reflectance at the surface and at the sensor), and (iii) inferring atmospheric transmission profiles, such as absorbing bands and their relative magnitudes.

Haldane Bundles: A Dataset for Learning to Predict the Chern Number of Line Bundles on the Torus

Characteristic classes, which are abstract topological invariants associated with vector bundles, have become an important notion in modern physics with surprising real-world consequences. As a representative example, the incredible properties of topological insulators, which are insulators in their bulk but conductors on their surface, can be completely characterized by a specific characteristic class associated with their electronic band structure, the first Chern class. Given their importance to next generation computing and the computational challenge of calculating them using first-principles approaches, there is a need to develop machine learning approaches to predict the characteristic classes associated with a material system. To aid in this program we introduce the {\emph{Haldane bundle dataset}}, which consists of synthetically generated complex line bundles on the $2$-torus. We envision this dataset, which is not as challenging as noisy and sparsely measured real-world datasets but (as we show) still difficult for off-the-shelf architectures, to be a testing ground for architectures that incorporate the rich topological and geometric priors underlying characteristic classes.

ICML 2023 Topological Deep Learning Challenge : Design and Results

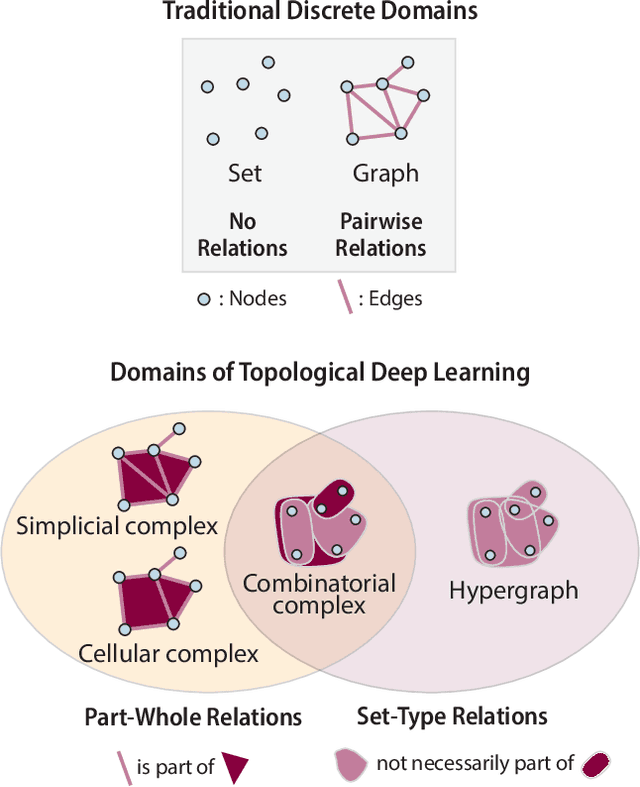
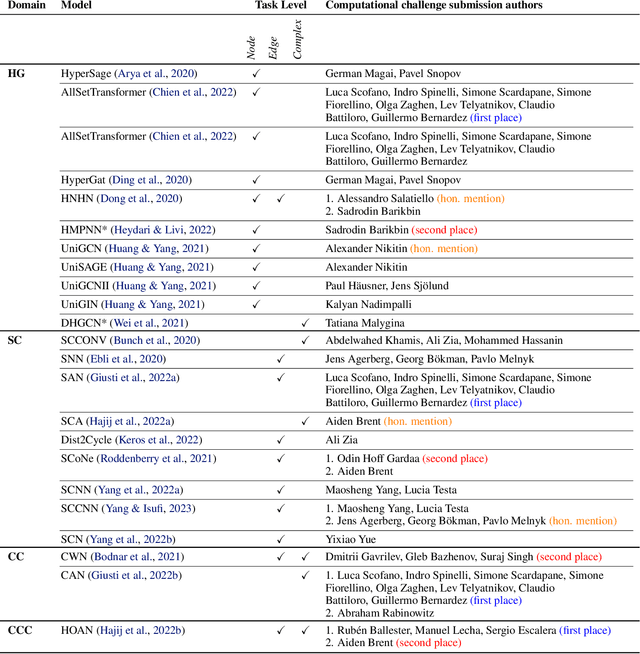
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.

Reproducing Kernel Hilbert Space Pruning for Sparse Hyperspectral Abundance Prediction

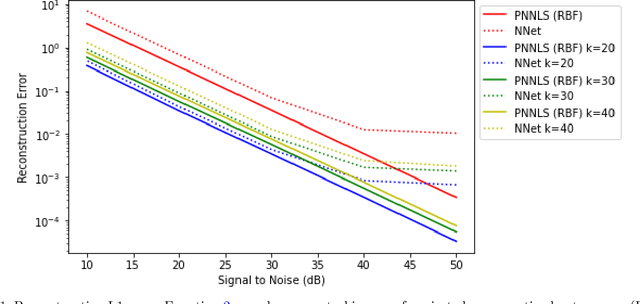
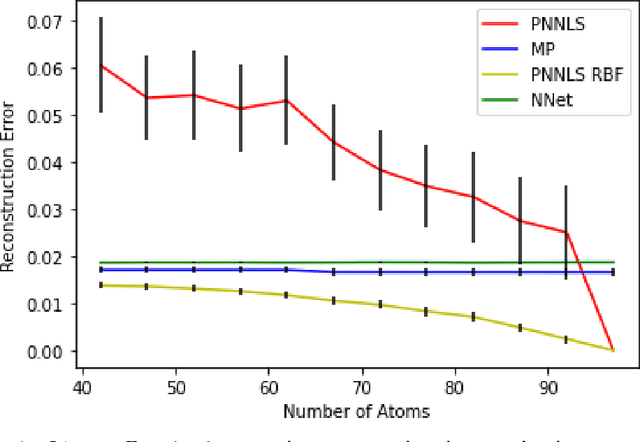
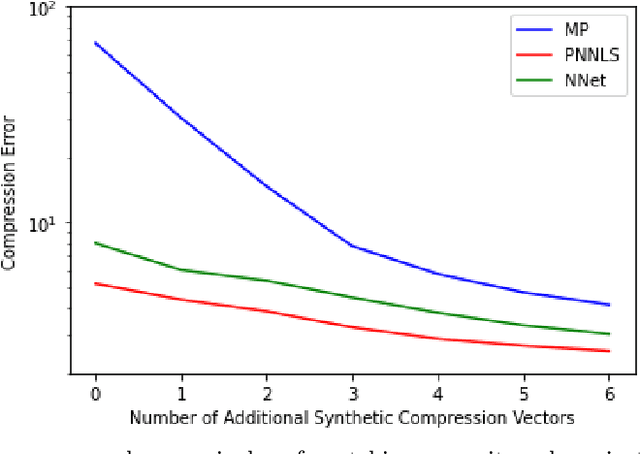
Hyperspectral measurements from long range sensors can give a detailed picture of the items, materials, and chemicals in a scene but analysis can be difficult, slow, and expensive due to high spatial and spectral resolutions of state-of-the-art sensors. As such, sparsity is important to enable the future of spectral compression and analytics. It has been observed that environmental and atmospheric effects, including scattering, can produce nonlinear effects posing challenges for existing source separation and compression methods. We present a novel transformation into Hilbert spaces for pruning and constructing sparse representations via non-negative least squares minimization. Then we introduce max likelihood compression vectors to decrease information loss. Our approach is benchmarked against standard pruning and least squares as well as deep learning methods. Our methods are evaluated in terms of overall spectral reconstruction error and compression rate using real and synthetic data. We find that pruning least squares methods converge quickly unlike matching pursuit methods. We find that Hilbert space pruning can reduce error by as much as 40% of the error of standard pruning and also outperform neural network autoencoders.

Neural frames: A Tool for Studying the Tangent Bundles Underlying Image Datasets and How Deep Learning Models Process Them

The assumption that many forms of high-dimensional data, such as images, actually live on low-dimensional manifolds, sometimes known as the manifold hypothesis, underlies much of our intuition for how and why deep learning works. Despite the central role that they play in our intuition, data manifolds are surprisingly hard to measure in the case of high-dimensional, sparsely sampled image datasets. This is particularly frustrating since the capability to measure data manifolds would provide a revealing window into the inner workings and dynamics of deep learning models. Motivated by this, we introduce neural frames, a novel and easy to use tool inspired by the notion of a frame from differential geometry. Neural frames can be used to explore the local neighborhoods of data manifolds as they pass through the hidden layers of neural networks even when one only has a single datapoint available. We present a mathematical framework for neural frames and explore some of their properties. We then use them to make a range of observations about how modern model architectures and training routines, such as heavy augmentation and adversarial training, affect the local behavior of a model.

Do Neural Networks Trained with Topological Features Learn Different Internal Representations?

There is a growing body of work that leverages features extracted via topological data analysis to train machine learning models. While this field, sometimes known as topological machine learning (TML), has seen some notable successes, an understanding of how the process of learning from topological features differs from the process of learning from raw data is still limited. In this work, we begin to address one component of this larger issue by asking whether a model trained with topological features learns internal representations of data that are fundamentally different than those learned by a model trained with the original raw data. To quantify ``different'', we exploit two popular metrics that can be used to measure the similarity of the hidden representations of data within neural networks, neural stitching and centered kernel alignment. From these we draw a range of conclusions about how training with topological features does and does not change the representations that a model learns. Perhaps unsurprisingly, we find that structurally, the hidden representations of models trained and evaluated on topological features differ substantially compared to those trained and evaluated on the corresponding raw data. On the other hand, our experiments show that in some cases, these representations can be reconciled (at least to the degree required to solve the corresponding task) using a simple affine transformation. We conjecture that this means that neural networks trained on raw data may extract some limited topological features in the process of making predictions.

On the Symmetries of Deep Learning Models and their Internal Representations

Symmetry has been a fundamental tool in the exploration of a broad range of complex systems. In machine learning, symmetry has been explored in both models and data. In this paper we seek to connect the symmetries arising from the architecture of a family of models with the symmetries of that family's internal representation of data. We do this by calculating a set of fundamental symmetry groups, which we call the \emph{intertwiner groups} of the model. Each of these arises from a particular nonlinear layer of the model and different nonlinearities result in different symmetry groups. These groups change the weights of a model in such a way that the underlying function that the model represents remains constant but the internal representations of data inside the model may change. We connect intertwiner groups to a model's internal representations of data through a range of experiments that probe similarities between hidden states across models with the same architecture. Our work suggests that the symmetries of a network are propagated into the symmetries in that network's representation of data, providing us with a better understanding of how architecture affects the learning and prediction process. Finally, we speculate that for ReLU networks, the intertwiner groups may provide a justification for the common practice of concentrating model interpretability exploration on the activation basis in hidden layers rather than arbitrary linear combinations thereof.