STARS: Sensor-agnostic Transformer Architecture for Remote Sensing

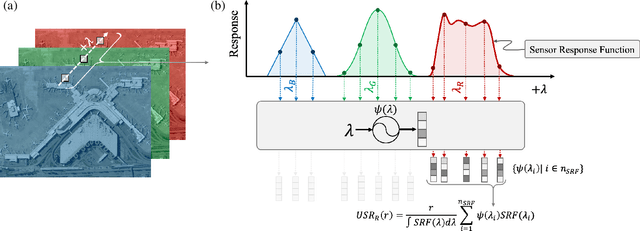
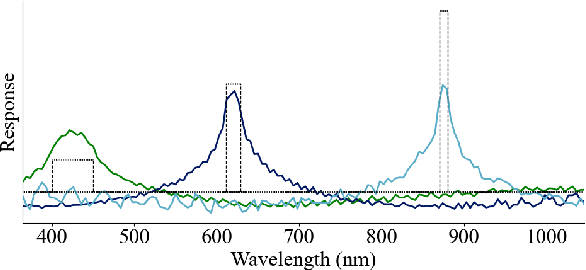
We present a sensor-agnostic spectral transformer as the basis for spectral foundation models. To that end, we introduce a Universal Spectral Representation (USR) that leverages sensor meta-data, such as sensing kernel specifications and sensing wavelengths, to encode spectra obtained from any spectral instrument into a common representation, such that a single model can ingest data from any sensor. Furthermore, we develop a methodology for pre-training such models in a self-supervised manner using a novel random sensor-augmentation and reconstruction pipeline to learn spectral features independent of the sensing paradigm. We demonstrate that our architecture can learn sensor independent spectral features that generalize effectively to sensors not seen during training. This work sets the stage for training foundation models that can both leverage and be effective for the growing diversity of spectral data.

Data-Driven Invertible Neural Surrogates of Atmospheric Transmission

We present a framework for inferring an atmospheric transmission profile from a spectral scene. This framework leverages a lightweight, physics-based simulator that is automatically tuned - by virtue of autodifferentiation and differentiable programming - to construct a surrogate atmospheric profile to model the observed data. We demonstrate utility of the methodology by (i) performing atmospheric correction, (ii) recasting spectral data between various modalities (e.g. radiance and reflectance at the surface and at the sensor), and (iii) inferring atmospheric transmission profiles, such as absorbing bands and their relative magnitudes.

Neural Differential Algebraic Equations

Differential-Algebraic Equations (DAEs) describe the temporal evolution of systems that obey both differential and algebraic constraints. Of particular interest are systems that contain implicit relationships between their components, such as conservation relationships. Here, we present Neural Differential-Algebraic Equations (NDAEs) suitable for data-driven modeling of DAEs. This methodology is built upon the concept of the Universal Differential Equation; that is, a model constructed as a system of Neural Ordinary Differential Equations informed by theory from particular science domains. In this work, we show that the proposed NDAEs abstraction is suitable for relevant system-theoretic data-driven modeling tasks. Presented examples include (i) the inverse problem of tank-manifold dynamics and (ii) discrepancy modeling of a network of pumps, tanks, and pipes. Our experiments demonstrate the proposed method's robustness to noise and extrapolation ability to (i) learn the behaviors of the system components and their interaction physics and (ii) disambiguate between data trends and mechanistic relationships contained in the system.

Neural Lumped Parameter Differential Equations with Application in Friction-Stir Processing

Lumped parameter methods aim to simplify the evolution of spatially-extended or continuous physical systems to that of a "lumped" element representative of the physical scales of the modeled system. For systems where the definition of a lumped element or its associated physics may be unknown, modeling tasks may be restricted to full-fidelity simulations of the physics of a system. In this work, we consider data-driven modeling tasks with limited point-wise measurements of otherwise continuous systems. We build upon the notion of the Universal Differential Equation (UDE) to construct data-driven models for reducing dynamics to that of a lumped parameter and inferring its properties. The flexibility of UDEs allow for composing various known physical priors suitable for application-specific modeling tasks, including lumped parameter methods. The motivating example for this work is the plunge and dwell stages for friction-stir welding; specifically, (i) mapping power input into the tool to a point-measurement of temperature and (ii) using this learned mapping for process control.

Physics-informed Machine Learning of Parameterized Fundamental Diagrams

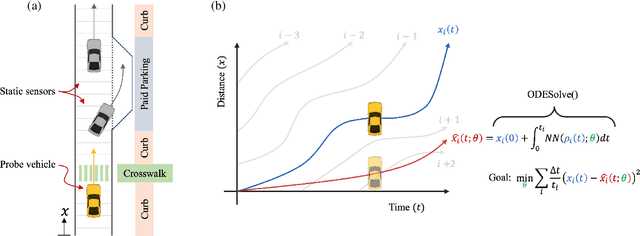
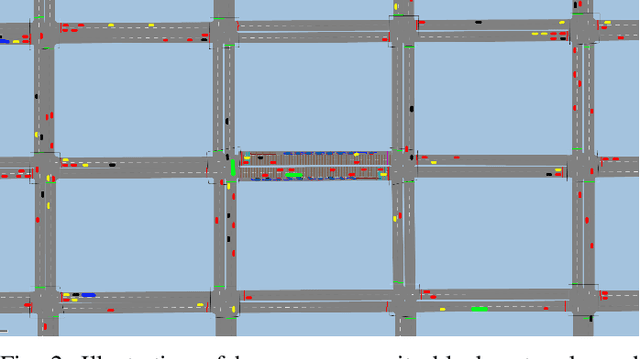
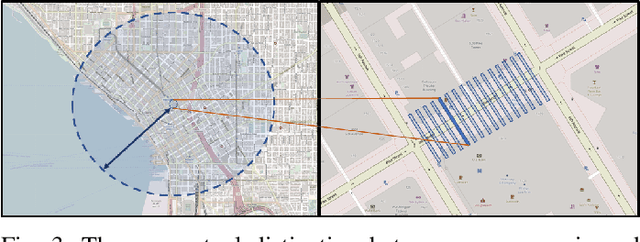
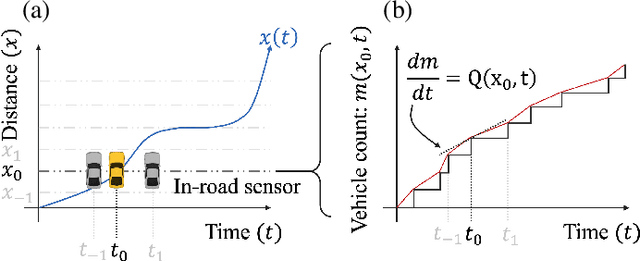
Fundamental diagrams describe the relationship between speed, flow, and density for some roadway (or set of roadway) configuration(s). These diagrams typically do not reflect, however, information on how speed-flow relationships change as a function of exogenous variables such as curb configuration, weather or other exogenous, contextual information. In this paper we present a machine learning methodology that respects known engineering constraints and physical laws of roadway flux - those that are captured in fundamental diagrams - and show how this can be used to introduce contextual information into the generation of these diagrams. The modeling task is formulated as a probe vehicle trajectory reconstruction problem with Neural Ordinary Differential Equations (Neural ODEs). With the presented methodology, we extend the fundamental diagram to non-idealized roadway segments with potentially obstructed traffic data. For simulated data, we generalize this relationship by introducing contextual information at the learning stage, i.e. vehicle composition, driver behavior, curb zoning configuration, etc, and show how the speed-flow relationship changes as a function of these exogenous factors independent of roadway design.

Structural Inference of Networked Dynamical Systems with Universal Differential Equations

Networked dynamical systems are common throughout science in engineering; e.g., biological networks, reaction networks, power systems, and the like. For many such systems, nonlinearity drives populations of identical (or near-identical) units to exhibit a wide range of nontrivial behaviors, such as the emergence of coherent structures (e.g., waves and patterns) or otherwise notable dynamics (e.g., synchrony and chaos). In this work, we seek to infer (i) the intrinsic physics of a base unit of a population, (ii) the underlying graphical structure shared between units, and (iii) the coupling physics of a given networked dynamical system given observations of nodal states. These tasks are formulated around the notion of the Universal Differential Equation, whereby unknown dynamical systems can be approximated with neural networks, mathematical terms known a priori (albeit with unknown parameterizations), or combinations of the two. We demonstrate the value of these inference tasks by investigating not only future state predictions but also the inference of system behavior on varied network topologies. The effectiveness and utility of these methods is shown with their application to canonical networked nonlinear coupled oscillators.