Differentiable Predictive Control for Robotics: A Data-Driven Predictive Safety Filter Approach

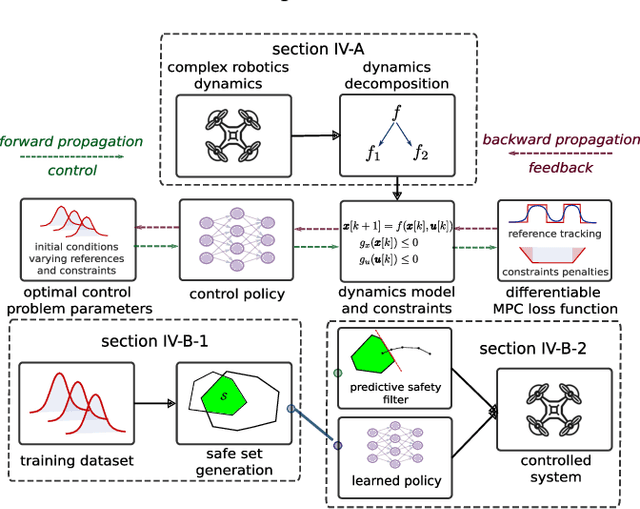
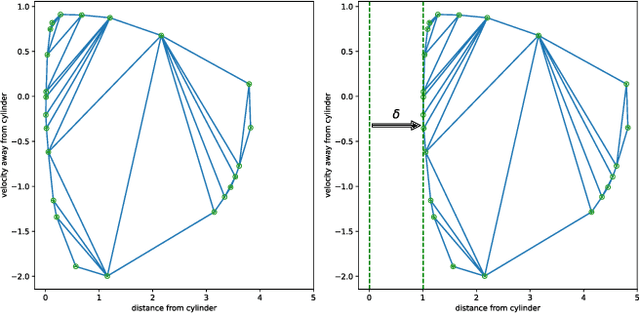
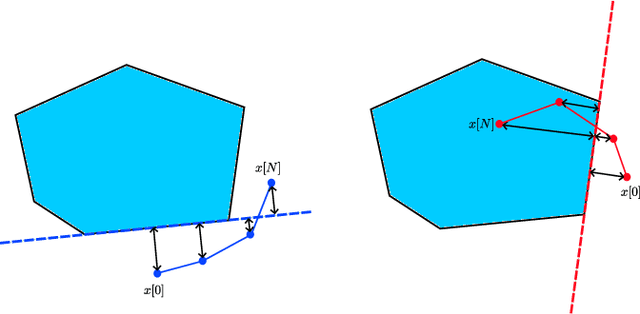
Model Predictive Control (MPC) is effective at generating safe control strategies in constrained scenarios, at the cost of computational complexity. This is especially the case in robots that require high sampling rates and have limited computing resources. Differentiable Predictive Control (DPC) trains offline a neural network approximation of the parametric MPC problem leading to computationally efficient online control laws at the cost of losing safety guarantees. DPC requires a differentiable model, and performs poorly when poorly conditioned. In this paper we propose a system decomposition technique based on relative degree to overcome this. We also develop a novel safe set generation technique based on the DPC training dataset and a novel event-triggered predictive safety filter which promotes convergence towards the safe set. Our empirical results on a quadcopter demonstrate that the DPC control laws have comparable performance to the state-of-the-art MPC whilst having up to three orders of magnitude reduction in computation time and satisfy safety requirements in a scenario that DPC was not trained on.

Metric Learning to Accelerate Convergence of Operator Splitting Methods for Differentiable Parametric Programming

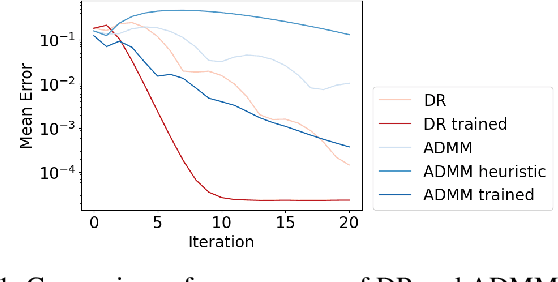
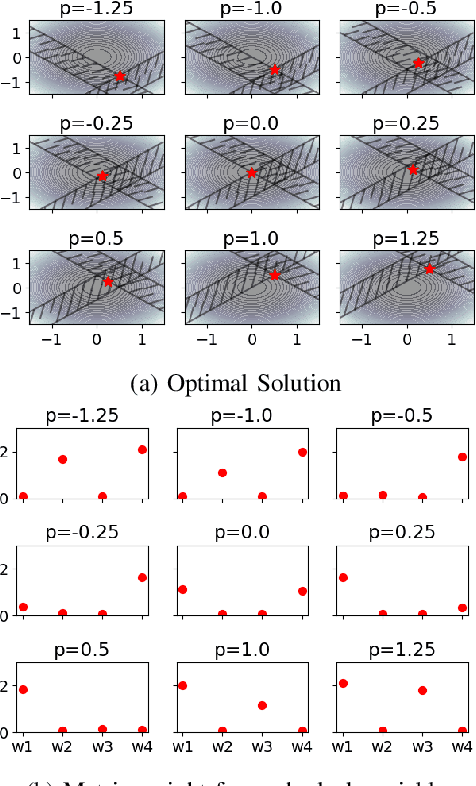
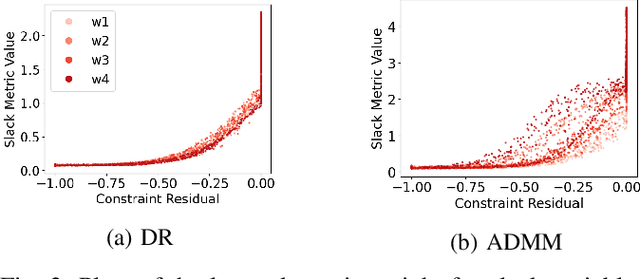
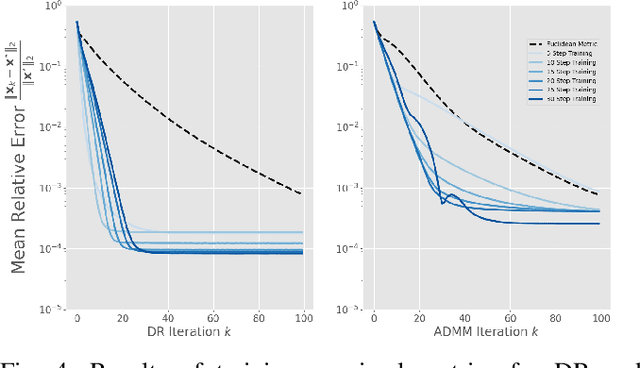
Recent work has shown a variety of ways in which machine learning can be used to accelerate the solution of constrained optimization problems. Increasing demand for real-time decision-making capabilities in applications such as artificial intelligence and optimal control has led to a variety of approaches, based on distinct strategies. This work proposes a novel approach to learning optimization, in which the underlying metric space of a proximal operator splitting algorithm is learned so as to maximize its convergence rate. While prior works in optimization theory have derived optimal metrics for limited classes of problems, the results do not extend to many practical problem forms including general Quadratic Programming (QP). This paper shows how differentiable optimization can enable the end-to-end learning of proximal metrics, enhancing the convergence of proximal algorithms for QP problems beyond what is possible based on known theory. Additionally, the results illustrate a strong connection between the learned proximal metrics and active constraints at the optima, leading to an interpretation in which the learning of proximal metrics can be viewed as a form of active set learning.

Neural Differential Algebraic Equations

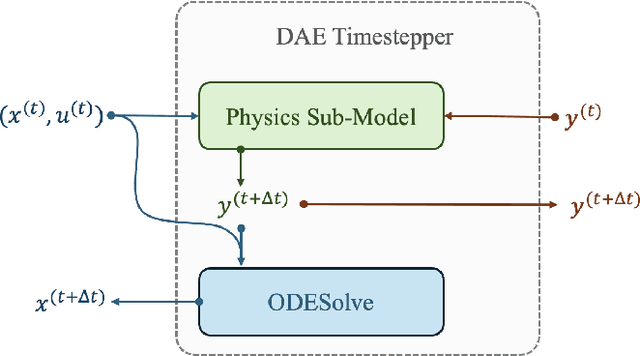
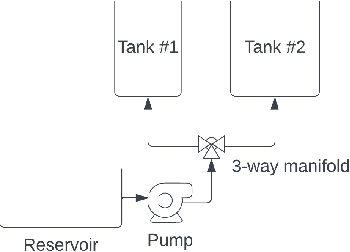
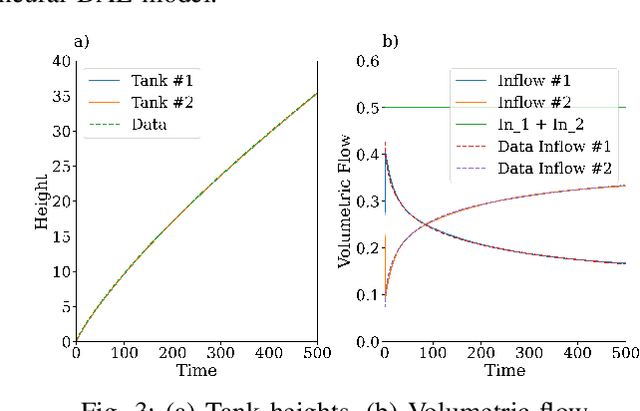
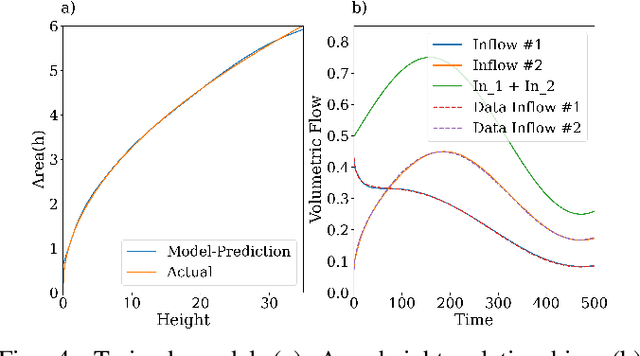
Differential-Algebraic Equations (DAEs) describe the temporal evolution of systems that obey both differential and algebraic constraints. Of particular interest are systems that contain implicit relationships between their components, such as conservation relationships. Here, we present Neural Differential-Algebraic Equations (NDAEs) suitable for data-driven modeling of DAEs. This methodology is built upon the concept of the Universal Differential Equation; that is, a model constructed as a system of Neural Ordinary Differential Equations informed by theory from particular science domains. In this work, we show that the proposed NDAEs abstraction is suitable for relevant system-theoretic data-driven modeling tasks. Presented examples include (i) the inverse problem of tank-manifold dynamics and (ii) discrepancy modeling of a network of pumps, tanks, and pipes. Our experiments demonstrate the proposed method's robustness to noise and extrapolation ability to (i) learn the behaviors of the system components and their interaction physics and (ii) disambiguate between data trends and mechanistic relationships contained in the system.

Semi-Supervised Learning of Dynamical Systems with Neural Ordinary Differential Equations: A Teacher-Student Model Approach

Modeling dynamical systems is crucial for a wide range of tasks, but it remains challenging due to complex nonlinear dynamics, limited observations, or lack of prior knowledge. Recently, data-driven approaches such as Neural Ordinary Differential Equations (NODE) have shown promising results by leveraging the expressive power of neural networks to model unknown dynamics. However, these approaches often suffer from limited labeled training data, leading to poor generalization and suboptimal predictions. On the other hand, semi-supervised algorithms can utilize abundant unlabeled data and have demonstrated good performance in classification and regression tasks. We propose TS-NODE, the first semi-supervised approach to modeling dynamical systems with NODE. TS-NODE explores cheaply generated synthetic pseudo rollouts to broaden exploration in the state space and to tackle the challenges brought by lack of ground-truth system data under a teacher-student model. TS-NODE employs an unified optimization framework that corrects the teacher model based on the student's feedback while mitigating the potential false system dynamics present in pseudo rollouts. TS-NODE demonstrates significant performance improvements over a baseline Neural ODE model on multiple dynamical system modeling tasks.

Extreme Risk Mitigation in Reinforcement Learning using Extreme Value Theory

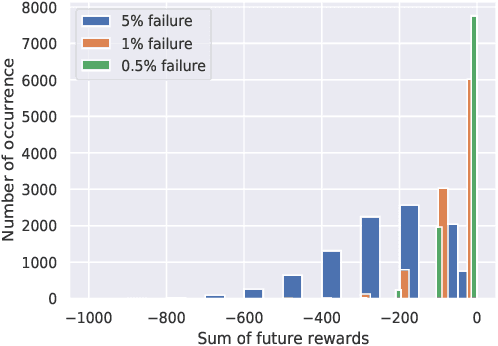
Risk-sensitive reinforcement learning (RL) has garnered significant attention in recent years due to the growing interest in deploying RL agents in real-world scenarios. A critical aspect of risk awareness involves modeling highly rare risk events (rewards) that could potentially lead to catastrophic outcomes. These infrequent occurrences present a formidable challenge for data-driven methods aiming to capture such risky events accurately. While risk-aware RL techniques do exist, their level of risk aversion heavily relies on the precision of the state-action value function estimation when modeling these rare occurrences. Our work proposes to enhance the resilience of RL agents when faced with very rare and risky events by focusing on refining the predictions of the extreme values predicted by the state-action value function distribution. To achieve this, we formulate the extreme values of the state-action value function distribution as parameterized distributions, drawing inspiration from the principles of extreme value theory (EVT). This approach effectively addresses the issue of infrequent occurrence by leveraging EVT-based parameterization. Importantly, we theoretically demonstrate the advantages of employing these parameterized distributions in contrast to other risk-averse algorithms. Our evaluations show that the proposed method outperforms other risk averse RL algorithms on a diverse range of benchmark tasks, each encompassing distinct risk scenarios.

Power Grid Behavioral Patterns and Risks of Generalization in Applied Machine Learning

Recent years have seen a rich literature of data-driven approaches designed for power grid applications. However, insufficient consideration of domain knowledge can impose a high risk to the practicality of the methods. Specifically, ignoring the grid-specific spatiotemporal patterns (in load, generation, and topology, etc.) can lead to outputting infeasible, unrealizable, or completely meaningless predictions on new inputs. To address this concern, this paper investigates real-world operational data to provide insights into power grid behavioral patterns, including the time-varying topology, load, and generation, as well as the spatial differences (in peak hours, diverse styles) between individual loads and generations. Then based on these observations, we evaluate the generalization risks in some existing ML works causedby ignoring these grid-specific patterns in model design and training.

Machine Learning for Smart and Energy-Efficient Buildings

Energy consumption in buildings, both residential and commercial, accounts for approximately 40% of all energy usage in the U.S., and similar numbers are being reported from countries around the world. This significant amount of energy is used to maintain a comfortable, secure, and productive environment for the occupants. So, it is crucial that the energy consumption in buildings must be optimized, all the while maintaining satisfactory levels of occupant comfort, health, and safety. Recently, Machine Learning has been proven to be an invaluable tool in deriving important insights from data and optimizing various systems. In this work, we review the ways in which machine learning has been leveraged to make buildings smart and energy-efficient. For the convenience of readers, we provide a brief introduction of several machine learning paradigms and the components and functioning of each smart building system we cover. Finally, we discuss challenges faced while implementing machine learning algorithms in smart buildings and provide future avenues for research at the intersection of smart buildings and machine learning.

Differentiable Predictive Control with Safety Guarantees: A Control Barrier Function Approach

We develop a novel form of differentiable predictive control (DPC) with safety and robustness guarantees based on control barrier functions. DPC is an unsupervised learning-based method for obtaining approximate solutions to explicit model predictive control (MPC) problems. In DPC, the predictive control policy parametrized by a neural network is optimized offline via direct policy gradients obtained by automatic differentiation of the MPC problem. The proposed approach exploits a new form of sampled-data barrier function to enforce offline and online safety requirements in DPC settings while only interrupting the neural network-based controller near the boundary of the safe set. The effectiveness of the proposed approach is demonstrated in simulation.

Structural Inference of Networked Dynamical Systems with Universal Differential Equations

Networked dynamical systems are common throughout science in engineering; e.g., biological networks, reaction networks, power systems, and the like. For many such systems, nonlinearity drives populations of identical (or near-identical) units to exhibit a wide range of nontrivial behaviors, such as the emergence of coherent structures (e.g., waves and patterns) or otherwise notable dynamics (e.g., synchrony and chaos). In this work, we seek to infer (i) the intrinsic physics of a base unit of a population, (ii) the underlying graphical structure shared between units, and (iii) the coupling physics of a given networked dynamical system given observations of nodal states. These tasks are formulated around the notion of the Universal Differential Equation, whereby unknown dynamical systems can be approximated with neural networks, mathematical terms known a priori (albeit with unknown parameterizations), or combinations of the two. We demonstrate the value of these inference tasks by investigating not only future state predictions but also the inference of system behavior on varied network topologies. The effectiveness and utility of these methods is shown with their application to canonical networked nonlinear coupled oscillators.

Neuro-physical dynamic load modeling using differentiable parametric optimization

In this work, we investigate a data-driven approach for obtaining a reduced equivalent load model of distribution systems for electromechanical transient stability analysis. The proposed reduced equivalent is a neuro-physical model comprising of a traditional ZIP load model augmented with a neural network. This neuro-physical model is trained through differentiable programming. We discuss the formulation, modeling details, and training of the proposed model set up as a differential parametric program. The performance and accuracy of this neurophysical ZIP load model is presented on a medium-scale 350-bus transmission-distribution network.