Differentiable Predictive Control for Robotics: A Data-Driven Predictive Safety Filter Approach

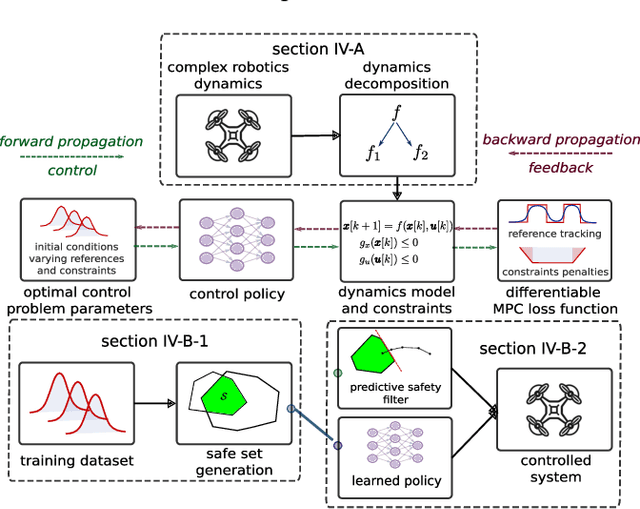
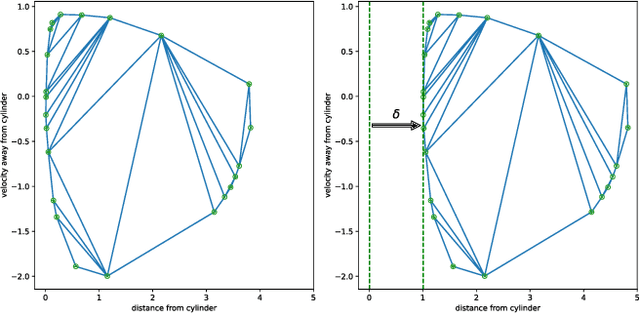
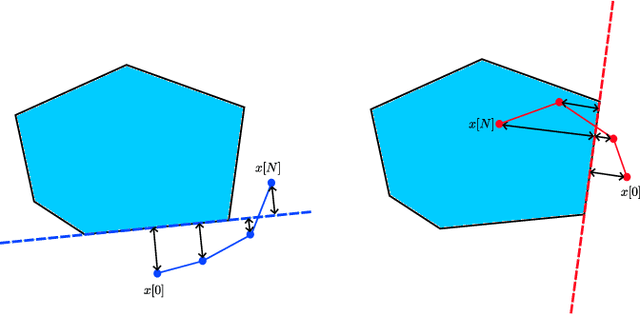
Model Predictive Control (MPC) is effective at generating safe control strategies in constrained scenarios, at the cost of computational complexity. This is especially the case in robots that require high sampling rates and have limited computing resources. Differentiable Predictive Control (DPC) trains offline a neural network approximation of the parametric MPC problem leading to computationally efficient online control laws at the cost of losing safety guarantees. DPC requires a differentiable model, and performs poorly when poorly conditioned. In this paper we propose a system decomposition technique based on relative degree to overcome this. We also develop a novel safe set generation technique based on the DPC training dataset and a novel event-triggered predictive safety filter which promotes convergence towards the safe set. Our empirical results on a quadcopter demonstrate that the DPC control laws have comparable performance to the state-of-the-art MPC whilst having up to three orders of magnitude reduction in computation time and satisfy safety requirements in a scenario that DPC was not trained on.

Differentiable Predictive Control for Large-Scale Urban Road Networks

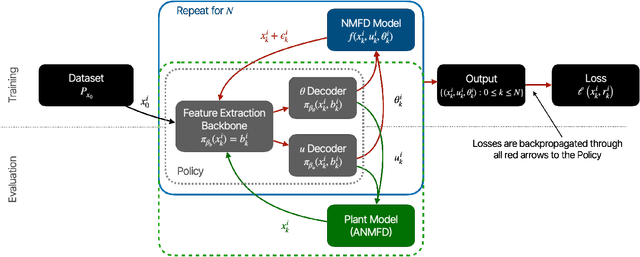
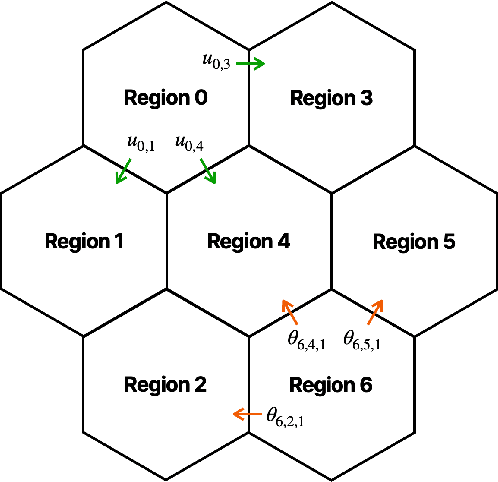
Transportation is a major contributor to CO2 emissions, making it essential to optimize traffic networks to reduce energy-related emissions. This paper presents a novel approach to traffic network control using Differentiable Predictive Control (DPC), a physics-informed machine learning methodology. We base our model on the Macroscopic Fundamental Diagram (MFD) and the Networked Macroscopic Fundamental Diagram (NMFD), offering a simplified representation of citywide traffic networks. Our approach ensures compliance with system constraints by construction. In empirical comparisons with existing state-of-the-art Model Predictive Control (MPC) methods, our approach demonstrates a 4 order of magnitude reduction in computation time and an up to 37% improvement in traffic performance. Furthermore, we assess the robustness of our controller to scenario shifts and find that it adapts well to changes in traffic patterns. This work proposes more efficient traffic control methods, particularly in large-scale urban networks, and aims to mitigate emissions and alleviate congestion in the future.

Physics-Informed Machine Learning for Modeling and Control of Dynamical Systems

Physics-informed machine learning (PIML) is a set of methods and tools that systematically integrate machine learning (ML) algorithms with physical constraints and abstract mathematical models developed in scientific and engineering domains. As opposed to purely data-driven methods, PIML models can be trained from additional information obtained by enforcing physical laws such as energy and mass conservation. More broadly, PIML models can include abstract properties and conditions such as stability, convexity, or invariance. The basic premise of PIML is that the integration of ML and physics can yield more effective, physically consistent, and data-efficient models. This paper aims to provide a tutorial-like overview of the recent advances in PIML for dynamical system modeling and control. Specifically, the paper covers an overview of the theory, fundamental concepts and methods, tools, and applications on topics of: 1) physics-informed learning for system identification; 2) physics-informed learning for control; 3) analysis and verification of PIML models; and 4) physics-informed digital twins. The paper is concluded with a perspective on open challenges and future research opportunities.

Domain-aware Control-oriented Neural Models for Autonomous Underwater Vehicles

Conventional physics-based modeling is a time-consuming bottleneck in control design for complex nonlinear systems like autonomous underwater vehicles (AUVs). In contrast, purely data-driven models, though convenient and quick to obtain, require a large number of observations and lack operational guarantees for safety-critical systems. Data-driven models leveraging available partially characterized dynamics have potential to provide reliable systems models in a typical data-limited scenario for high value complex systems, thereby avoiding months of expensive expert modeling time. In this work we explore this middle-ground between expert-modeled and pure data-driven modeling. We present control-oriented parametric models with varying levels of domain-awareness that exploit known system structure and prior physics knowledge to create constrained deep neural dynamical system models. We employ universal differential equations to construct data-driven blackbox and graybox representations of the AUV dynamics. In addition, we explore a hybrid formulation that explicitly models the residual error related to imperfect graybox models. We compare the prediction performance of the learned models for different distributions of initial conditions and control inputs to assess their accuracy, generalization, and suitability for control.

Differentiable Predictive Control with Safety Guarantees: A Control Barrier Function Approach

We develop a novel form of differentiable predictive control (DPC) with safety and robustness guarantees based on control barrier functions. DPC is an unsupervised learning-based method for obtaining approximate solutions to explicit model predictive control (MPC) problems. In DPC, the predictive control policy parametrized by a neural network is optimized offline via direct policy gradients obtained by automatic differentiation of the MPC problem. The proposed approach exploits a new form of sampled-data barrier function to enforce offline and online safety requirements in DPC settings while only interrupting the neural network-based controller near the boundary of the safe set. The effectiveness of the proposed approach is demonstrated in simulation.

Safe, Passive Control for Mechanical Systems with Application to Physical Human-Robot Interactions

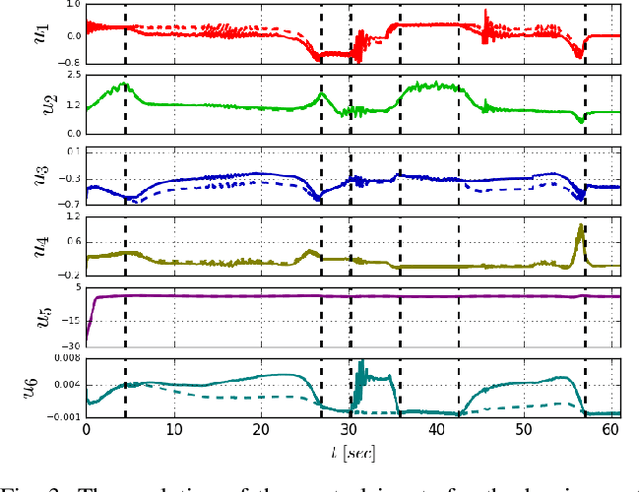
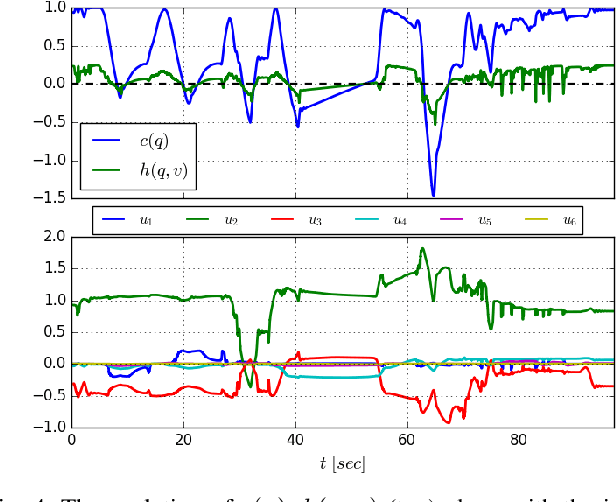
In this paper, we propose a novel safe, passive, and robust control law for mechanical systems. The proposed approach addresses safety from a physical human-robot interaction perspective, where a robot must not only stay inside a pre-defined region, but respect velocity constraints and ensure passivity with respect to external perturbations that may arise from a human or the environment. The proposed control is written in closed-form, behaves well even during singular configurations, and allows any nominal control law to be applied inside the operating region as long as the safety requirements (e.g., velocity) are adhered to. The proposed method is implemented on a 6-DOF robot to demonstrate its effectiveness during a physical human-robot interaction task.

Control Barrier Functions for Mechanical Systems: Theory and Application to Robotic Grasping

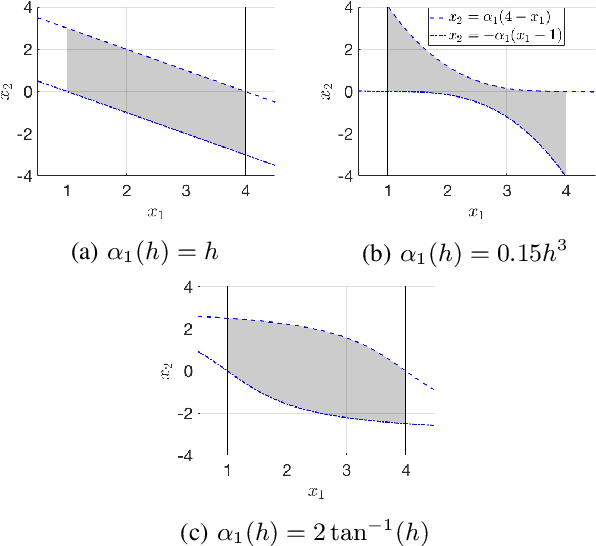
Control barrier functions have been demonstrated to be a useful method of ensuring constraint satisfaction for a wide class of controllers, however existing results are mostly restricted to continuous time systems of relative degree one. Mechanical systems, including robots, are typically second-order systems in which the control occurs at the force/torque level. These systems have velocity and position constraints (i.e. relative degree two) that are vital for safety and/or task execution. Additionally, mechanical systems are typically controlled digitally as sampled-data systems. The contribution of this work is two-fold. First, is the development of novel, robust control barrier functions that ensure constraint satisfaction for relative degree two, sampled-data systems in the presence of model uncertainty. Second, is the application of the proposed method to the challenging problem of robotic grasping in which a robotic hand must ensure an object remains inside the grasp while manipulating it to a desired reference trajectory. A grasp constraint satisfying controller is proposed that can admit existing nominal manipulation controllers from the literature, while simultaneously ensuring no slip, no over-extension (e.g. singular configurations), and no rolling off of the fingertips. Simulation and experimental results validate the proposed control for the robotic hand application.

Grasp Constraint Satisfaction for Object Manipulation using Robotic Hands

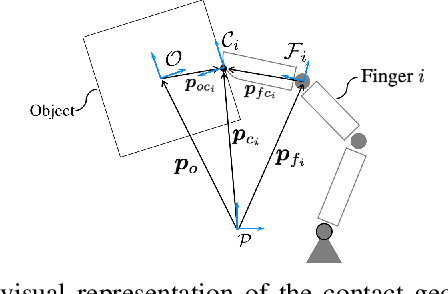
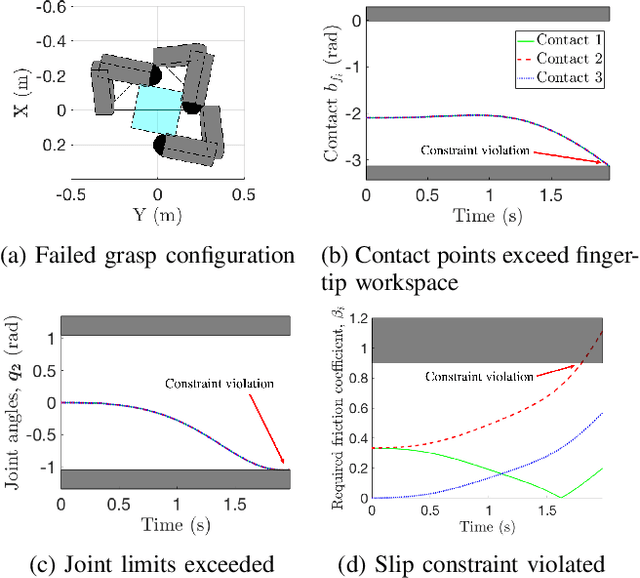
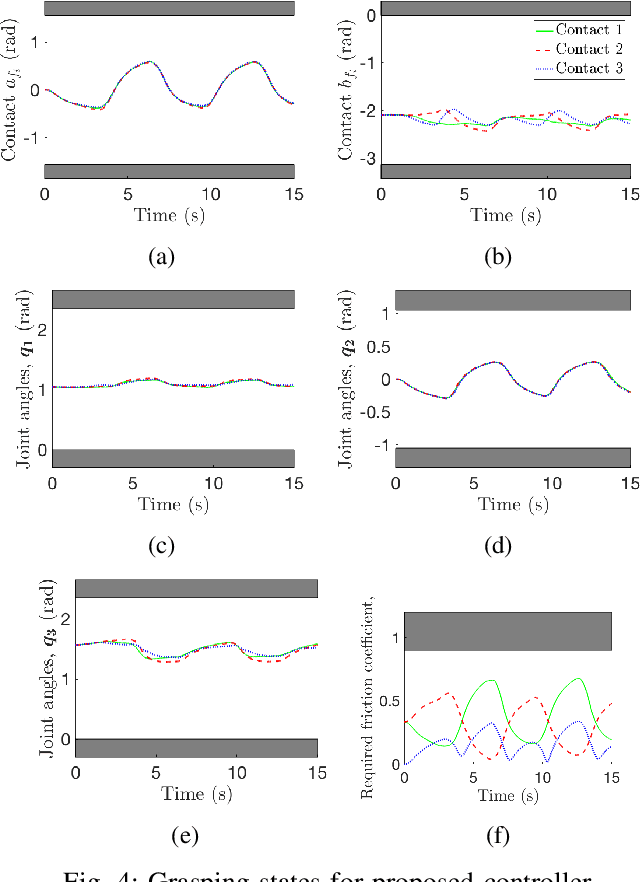
For successful object manipulation with robotic hands, it is important to ensure that the object remains in the grasp at all times. In addition to grasp constraints associated with slipping and singular hand configurations, excessive rolling is an important grasp concern where the contact points roll off of the fingertip surface. Related literature focus only on a subset of grasp constraints, or assume grasp constraint satisfaction without providing guarantees of such a claim. In this paper, we propose a control approach that systematically handles all grasp constraints. The proposed controller ensures that the object does not slip, joints do not exceed joint angle constraints (e.g. reach singular configurations), and the contact points remain in the fingertip workspace. The proposed controller accepts a nominal manipulation control, and ensures the grasping constraints are satisfied to support the assumptions made in the literature. Simulation results validate the proposed approach.