Safe Reinforcement Learning with Minimal Supervision

Reinforcement learning (RL) in the real world necessitates the development of procedures that enable agents to explore without causing harm to themselves or others. The most successful solutions to the problem of safe RL leverage offline data to learn a safe-set, enabling safe online exploration. However, this approach to safe-learning is often constrained by the demonstrations that are available for learning. In this paper we investigate the influence of the quantity and quality of data used to train the initial safe learning problem offline on the ability to learn safe-RL policies online. Specifically, we focus on tasks with spatially extended goal states where we have few or no demonstrations available. Classically this problem is addressed either by using hand-designed controllers to generate data or by collecting user-generated demonstrations. However, these methods are often expensive and do not scale to more complex tasks and environments. To address this limitation we propose an unsupervised RL-based offline data collection procedure, to learn complex and scalable policies without the need for hand-designed controllers or user demonstrations. Our research demonstrates the significance of providing sufficient demonstrations for agents to learn optimal safe-RL policies online, and as a result, we propose optimistic forgetting, a novel online safe-RL approach that is practical for scenarios with limited data. Further, our unsupervised data collection approach highlights the need to balance diversity and optimality for safe online exploration.

Differentiable Predictive Control for Robotics: A Data-Driven Predictive Safety Filter Approach

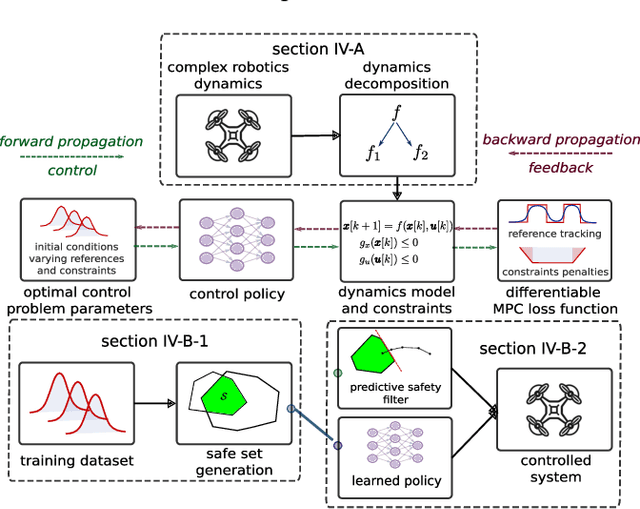
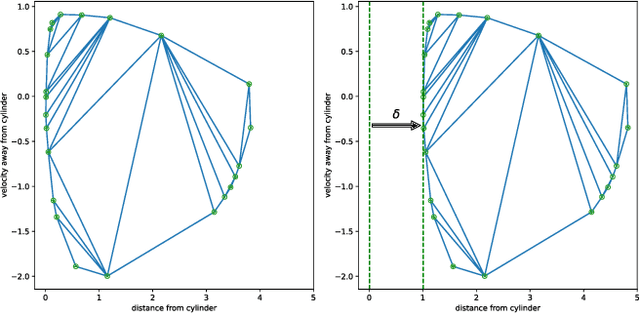
Model Predictive Control (MPC) is effective at generating safe control strategies in constrained scenarios, at the cost of computational complexity. This is especially the case in robots that require high sampling rates and have limited computing resources. Differentiable Predictive Control (DPC) trains offline a neural network approximation of the parametric MPC problem leading to computationally efficient online control laws at the cost of losing safety guarantees. DPC requires a differentiable model, and performs poorly when poorly conditioned. In this paper we propose a system decomposition technique based on relative degree to overcome this. We also develop a novel safe set generation technique based on the DPC training dataset and a novel event-triggered predictive safety filter which promotes convergence towards the safe set. Our empirical results on a quadcopter demonstrate that the DPC control laws have comparable performance to the state-of-the-art MPC whilst having up to three orders of magnitude reduction in computation time and satisfy safety requirements in a scenario that DPC was not trained on.

Imitation Learning of Stabilizing Policies for Nonlinear Systems

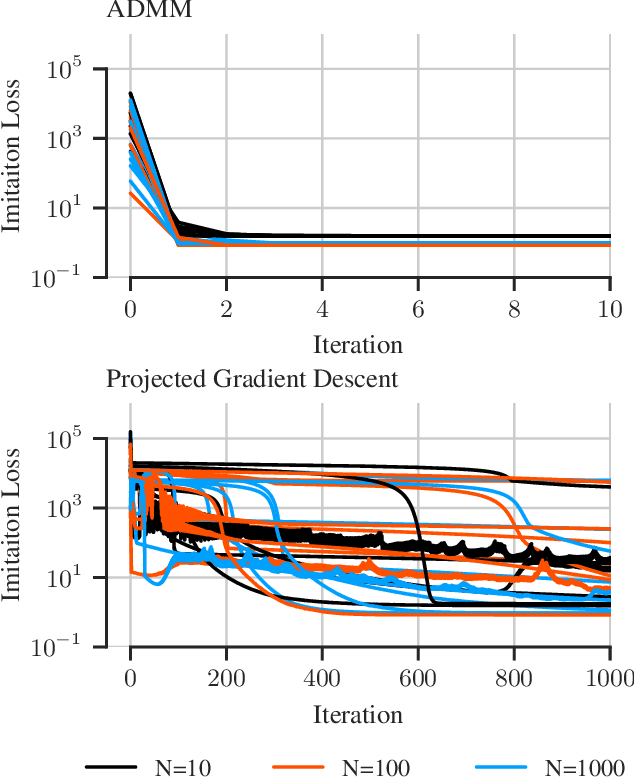
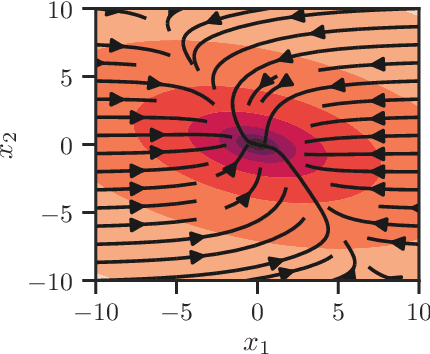
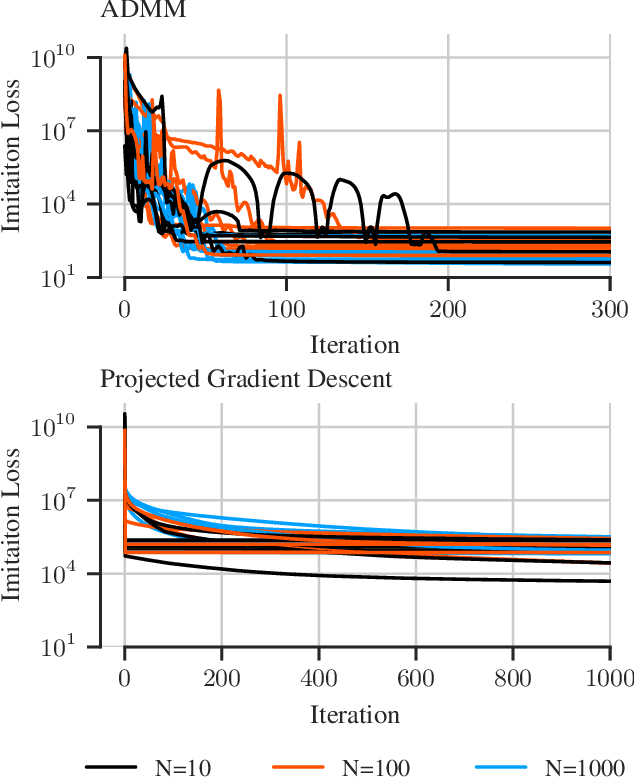
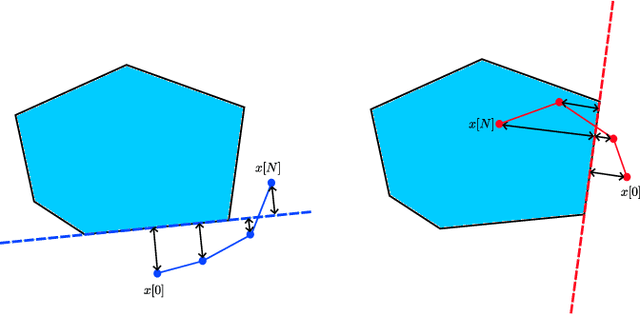
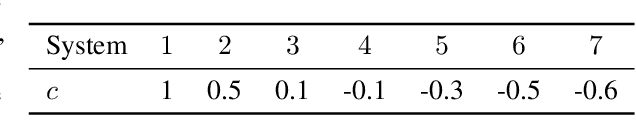
There has been a recent interest in imitation learning methods that are guaranteed to produce a stabilizing control law with respect to a known system. Work in this area has generally considered linear systems and controllers, for which stabilizing imitation learning takes the form of a biconvex optimization problem. In this paper it is demonstrated that the same methods developed for linear systems and controllers can be readily extended to polynomial systems and controllers using sum of squares techniques. A projected gradient descent algorithm and an alternating direction method of multipliers algorithm are proposed as heuristics for solving the stabilizing imitation learning problem, and their performance is illustrated through numerical experiments.

Infinite-Horizon Differentiable Model Predictive Control

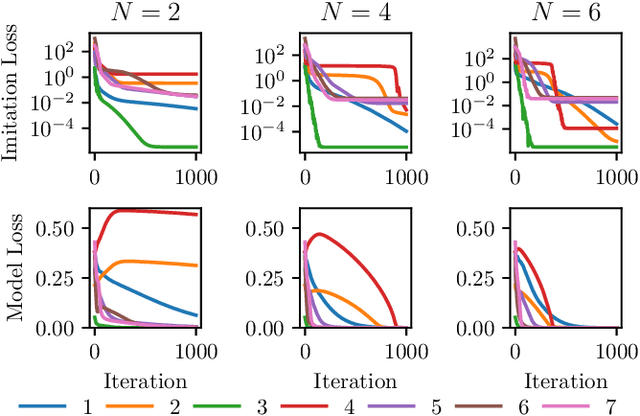
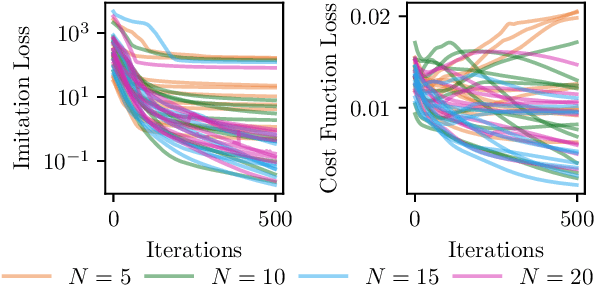
This paper proposes a differentiable linear quadratic Model Predictive Control (MPC) framework for safe imitation learning. The infinite-horizon cost is enforced using a terminal cost function obtained from the discrete-time algebraic Riccati equation (DARE), so that the learned controller can be proven to be stabilizing in closed-loop. A central contribution is the derivation of the analytical derivative of the solution of the DARE, thereby allowing the use of differentiation-based learning methods. A further contribution is the structure of the MPC optimization problem: an augmented Lagrangian method ensures that the MPC optimization is feasible throughout training whilst enforcing hard constraints on state and input, and a pre-stabilizing controller ensures that the MPC solution and derivatives are accurate at each iteration. The learning capabilities of the framework are demonstrated in a set of numerical studies.