Imitation Learning of Stabilizing Policies for Nonlinear Systems
Paper and Code
Sep 22, 2021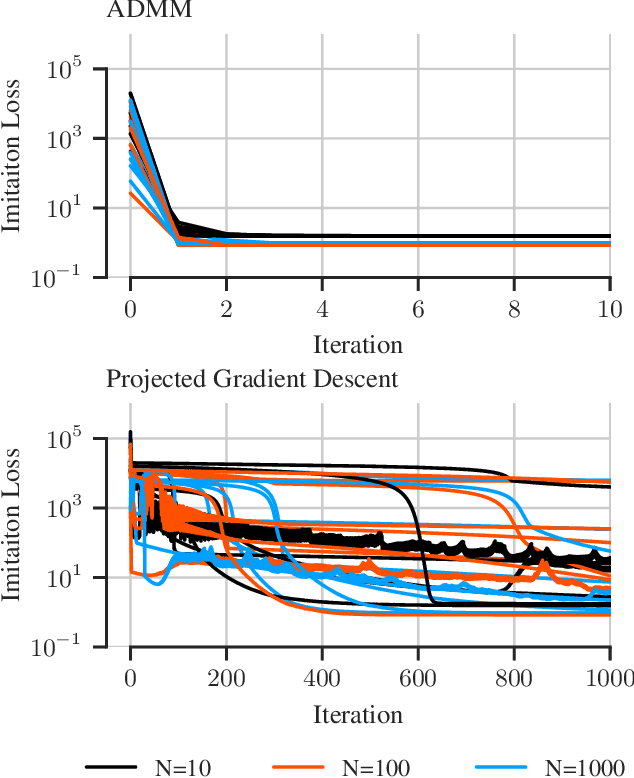
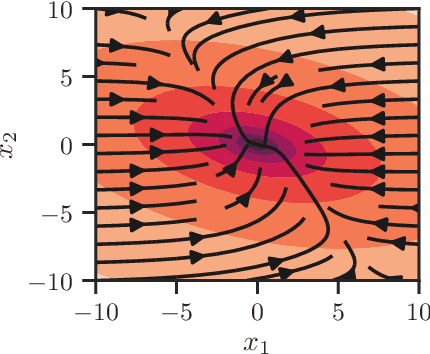
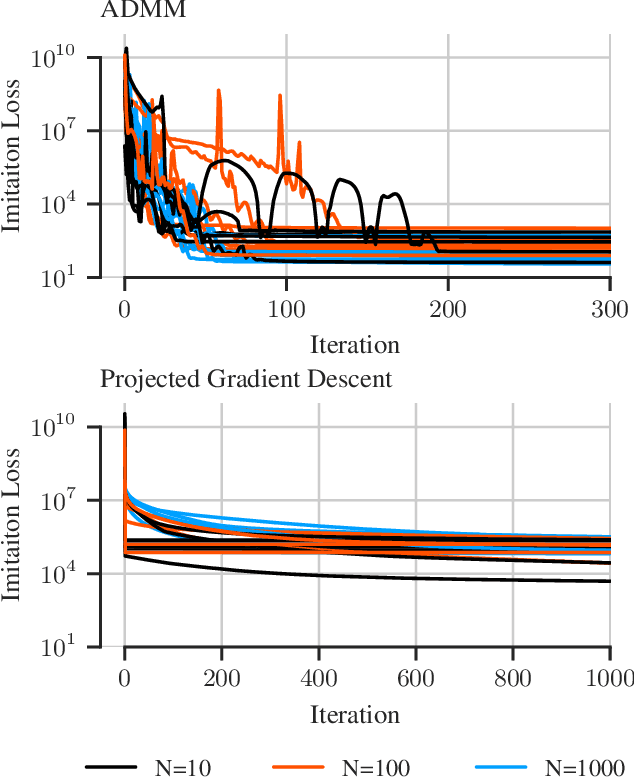
There has been a recent interest in imitation learning methods that are guaranteed to produce a stabilizing control law with respect to a known system. Work in this area has generally considered linear systems and controllers, for which stabilizing imitation learning takes the form of a biconvex optimization problem. In this paper it is demonstrated that the same methods developed for linear systems and controllers can be readily extended to polynomial systems and controllers using sum of squares techniques. A projected gradient descent algorithm and an alternating direction method of multipliers algorithm are proposed as heuristics for solving the stabilizing imitation learning problem, and their performance is illustrated through numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge