On the adaptation of recurrent neural networks for system identification

This paper presents a transfer learning approach which enables fast and efficient adaptation of Recurrent Neural Network (RNN) models of dynamical systems. A nominal RNN model is first identified using available measurements. The system dynamics are then assumed to change, leading to an unacceptable degradation of the nominal model performance on the perturbed system. To cope with the mismatch, the model is augmented with an additive correction term trained on fresh data from the new dynamic regime. The correction term is learned through a Jacobian Feature Regression (JFR) method defined in terms of the features spanned by the model's Jacobian with respect to its nominal parameters. A non-parametric view of the approach is also proposed, which extends recent work on Gaussian Process (GP) with Neural Tangent Kernel (NTK-GP) to the RNN case (RNTK-GP). This can be more efficient for very large networks or when only few data points are available. Implementation aspects for fast and efficient computation of the correction term, as well as the initial state estimation for the RNN model are described. Numerical examples show the effectiveness of the proposed methodology in presence of significant system variations.

Real-time Classification from Short Event-Camera Streams using Input-filtering Neural ODEs

Event-based cameras are novel, efficient sensors inspired by the human vision system, generating an asynchronous, pixel-wise stream of data. Learning from such data is generally performed through heavy preprocessing and event integration into images. This requires buffering of possibly long sequences and can limit the response time of the inference system. In this work, we instead propose to directly use events from a DVS camera, a stream of intensity changes and their spatial coordinates. This sequence is used as the input for a novel \emph{asynchronous} RNN-like architecture, the Input-filtering Neural ODEs (INODE). This is inspired by the dynamical systems and filtering literature. INODE is an extension of Neural ODEs (NODE) that allows for input signals to be continuously fed to the network, like in filtering. The approach naturally handles batches of time series with irregular time-stamps by implementing a batch forward Euler solver. INODE is trained like a standard RNN, it learns to discriminate short event sequences and to perform event-by-event online inference. We demonstrate our approach on a series of classification tasks, comparing against a set of LSTM baselines. We show that, independently of the camera resolution, INODE can outperform the baselines by a large margin on the ASL task and it's on par with a much larger LSTM for the NCALTECH task. Finally, we show that INODE is accurate even when provided with very few events.

Neural Lyapunov Model Predictive Control

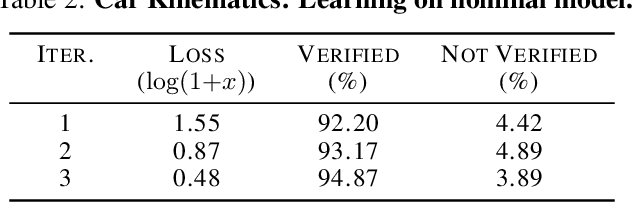
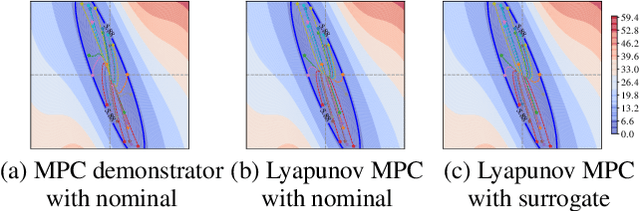
This paper presents Neural Lyapunov MPC, an algorithm to alternately train a Lyapunov neural network and a stabilising constrained Model Predictive Controller (MPC), given a neural network model of the system dynamics. This extends recent works on Lyapunov networks to be able to train solely from expert demonstrations of one-step transitions. The learned Lyapunov network is used as the value function for the MPC in order to guarantee stability and extend the stable region. Formal results are presented on the existence of a set of MPC parameters, such as discount factors, that guarantees stability with a horizon as short as one. Robustness margins are also discussed and existing performance bounds on value function MPC are extended to the case of imperfect models. The approach is tested on unstable non-linear continuous control tasks with hard constraints. Results demonstrate that, when a neural network trained on short sequences is used for predictions, a one-step horizon Neural Lyapunov MPC can successfully reproduce the expert behaviour and significantly outperform longer horizon MPCs.

Infinite-Horizon Differentiable Model Predictive Control

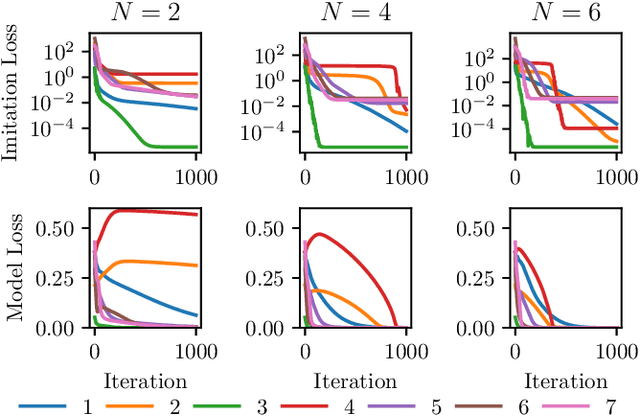
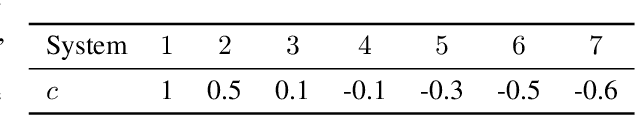
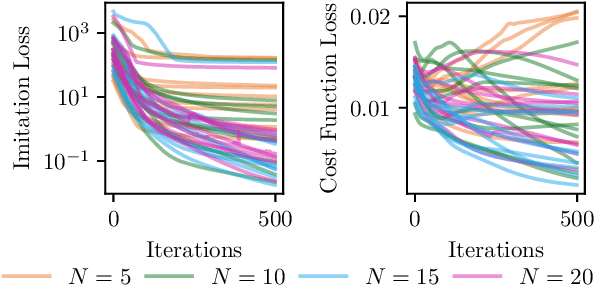
This paper proposes a differentiable linear quadratic Model Predictive Control (MPC) framework for safe imitation learning. The infinite-horizon cost is enforced using a terminal cost function obtained from the discrete-time algebraic Riccati equation (DARE), so that the learned controller can be proven to be stabilizing in closed-loop. A central contribution is the derivation of the analytical derivative of the solution of the DARE, thereby allowing the use of differentiation-based learning methods. A further contribution is the structure of the MPC optimization problem: an augmented Lagrangian method ensures that the MPC optimization is feasible throughout training whilst enforcing hard constraints on state and input, and a pre-stabilizing controller ensures that the MPC solution and derivatives are accurate at each iteration. The learning capabilities of the framework are demonstrated in a set of numerical studies.

Safe Interactive Model-Based Learning

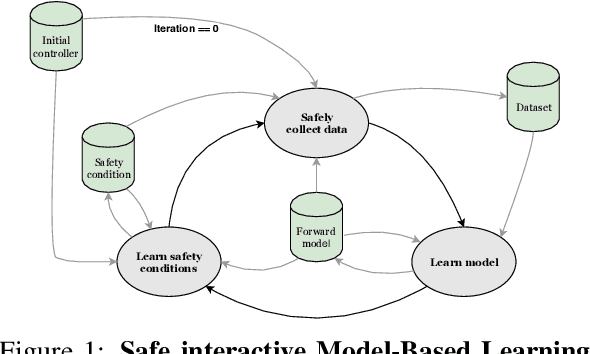
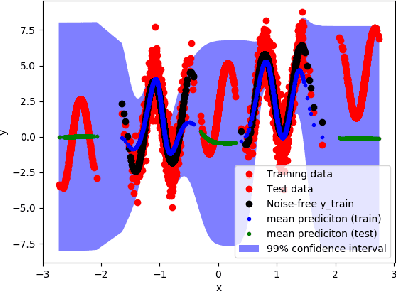
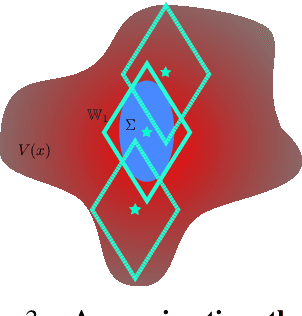
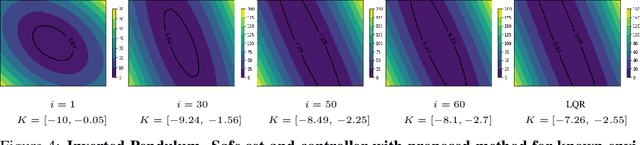
Control applications present hard operational constraints. A violation of these can result in unsafe behavior. This paper introduces Safe Interactive Model Based Learning (SiMBL), a framework to refine an existing controller and a system model while operating on the real environment. SiMBL is composed of the following trainable components: a Lyapunov function, which determines a safe set; a safe control policy; and a Bayesian RNN forward model. A min-max control framework, based on alternate minimisation and backpropagation through the forward model, is used for the offline computation of the controller and the safe set. Safety is formally verified a-posteriori with a probabilistic method that utilizes the Noise Contrastive Priors (NPC) idea to build a Bayesian RNN forward model with an additive state uncertainty estimate which is large outside the training data distribution. Iterative refinement of the model and the safe set is achieved thanks to a novel loss that conditions the uncertainty estimates of the new model to be close to the current one. The learned safe set and model can also be used for safe exploration, i.e., to collect data within the safe invariant set, for which a simple one-step MPC is proposed. The single components are tested on the simulation of an inverted pendulum with limited torque and stability region, showing that iteratively adding more data can improve the model, the controller and the size of the safe region.

Tustin neural networks: a class of recurrent nets for adaptive MPC of mechanical systems

The use of recurrent neural networks to represent the dynamics of unstable systems is difficult due to the need to properly initialize their internal states, which in most of the cases do not have any physical meaning, consequent to the non-smoothness of the optimization problem. For this reason, in this paper focus is placed on mechanical systems characterized by a number of degrees of freedom, each one represented by two states, namely position and velocity. For these systems, a new recurrent neural network is proposed: Tustin-Net. Inspired by second-order dynamics, the network hidden states can be straightforwardly estimated, as their differential relationships with the measured states are hardcoded in the forward pass. The proposed structure is used to model a double inverted pendulum and for model-based Reinforcement Learning, where an adaptive Model Predictive Controller scheme using the Unscented Kalman Filter is proposed to deal with parameter changes in the system.

Accelerating Neural ODEs with Spectral Elements

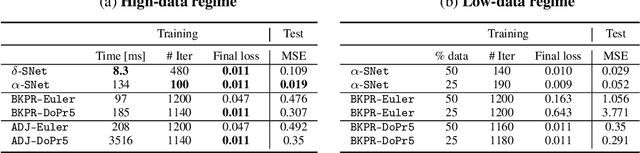
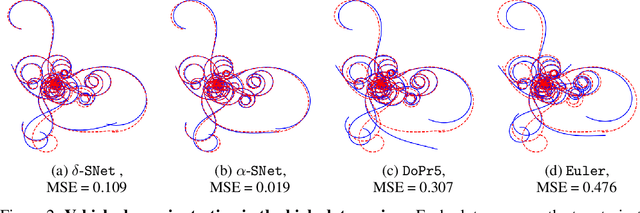
This paper proposes the use of spectral element methods \citep{canuto_spectral_1988} for fast and accurate training of Neural Ordinary Differential Equations (ODE-Nets; \citealp{Chen2018NeuralOD}). This is achieved by expressing their dynamics as truncated series of Legendre polynomials. The series coefficients, as well as the network weights, are computed by minimizing the weighted sum of the loss function and the violation of the ODE-Net dynamics. The problem is solved by coordinate descent that alternately minimizes, with respect to the coefficients and the weights, two unconstrained sub-problems using standard backpropagation and gradient methods. The resulting optimization scheme is fully time-parallel and results in a low memory footprint. Experimental comparison to standard methods, such as backpropagation through explicit solvers and the adjoint technique \citep{Chen2018NeuralOD}, on training surrogate models of small and medium-scale dynamical systems shows that it is at least one order of magnitude faster at reaching a comparable value of the loss function. The corresponding testing MSE is one order of magnitude smaller as well, suggesting generalization capabilities increase.

NAIS-Net: Stable Deep Networks from Non-Autonomous Differential Equations

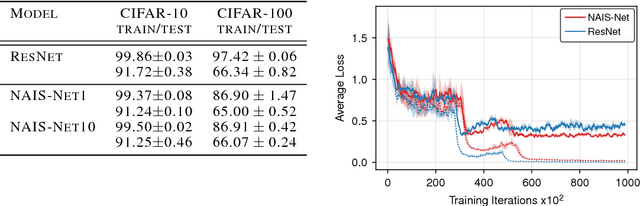
This paper introduces Non-Autonomous Input-Output Stable Network (NAIS-Net), a very deep architecture where each stacked processing block is derived from a time-invariant non-autonomous dynamical system. Non-autonomy is implemented by skip connections from the block input to each of the unrolled processing stages and allows stability to be enforced so that blocks can be unrolled adaptively to a pattern-dependent processing depth. NAIS-Net induces non-trivial, Lipschitz input-output maps, even for an infinite unroll length. We prove that the network is globally asymptotically stable so that for every initial condition there is exactly one input-dependent equilibrium assuming tanh units, and multiple stable equilibria for ReL units. An efficient implementation that enforces the stability under derived conditions for both fully-connected and convolutional layers is also presented. Experimental results show how NAIS-Net exhibits stability in practice, yielding a significant reduction in generalization gap compared to ResNets.