Neural Lyapunov Model Predictive Control

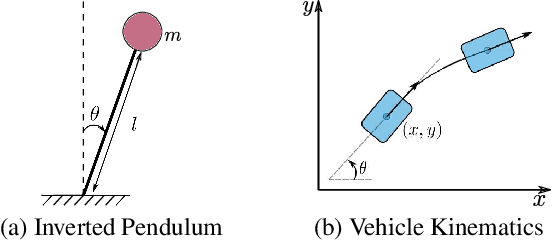
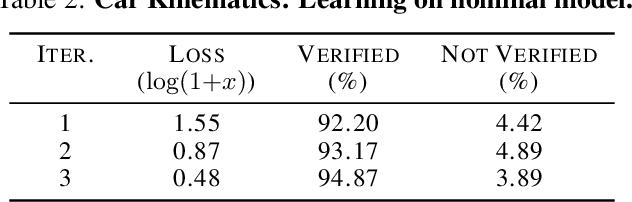
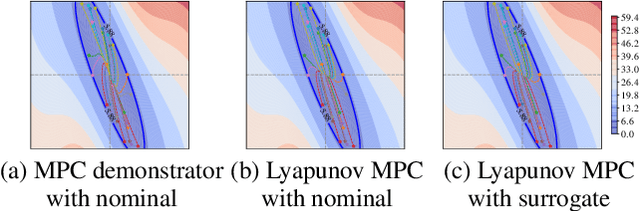
This paper presents Neural Lyapunov MPC, an algorithm to alternately train a Lyapunov neural network and a stabilising constrained Model Predictive Controller (MPC), given a neural network model of the system dynamics. This extends recent works on Lyapunov networks to be able to train solely from expert demonstrations of one-step transitions. The learned Lyapunov network is used as the value function for the MPC in order to guarantee stability and extend the stable region. Formal results are presented on the existence of a set of MPC parameters, such as discount factors, that guarantees stability with a horizon as short as one. Robustness margins are also discussed and existing performance bounds on value function MPC are extended to the case of imperfect models. The approach is tested on unstable non-linear continuous control tasks with hard constraints. Results demonstrate that, when a neural network trained on short sequences is used for predictions, a one-step horizon Neural Lyapunov MPC can successfully reproduce the expert behaviour and significantly outperform longer horizon MPCs.