Real-time Classification from Short Event-Camera Streams using Input-filtering Neural ODEs

Event-based cameras are novel, efficient sensors inspired by the human vision system, generating an asynchronous, pixel-wise stream of data. Learning from such data is generally performed through heavy preprocessing and event integration into images. This requires buffering of possibly long sequences and can limit the response time of the inference system. In this work, we instead propose to directly use events from a DVS camera, a stream of intensity changes and their spatial coordinates. This sequence is used as the input for a novel \emph{asynchronous} RNN-like architecture, the Input-filtering Neural ODEs (INODE). This is inspired by the dynamical systems and filtering literature. INODE is an extension of Neural ODEs (NODE) that allows for input signals to be continuously fed to the network, like in filtering. The approach naturally handles batches of time series with irregular time-stamps by implementing a batch forward Euler solver. INODE is trained like a standard RNN, it learns to discriminate short event sequences and to perform event-by-event online inference. We demonstrate our approach on a series of classification tasks, comparing against a set of LSTM baselines. We show that, independently of the camera resolution, INODE can outperform the baselines by a large margin on the ASL task and it's on par with a much larger LSTM for the NCALTECH task. Finally, we show that INODE is accurate even when provided with very few events.

Neural Lyapunov Model Predictive Control

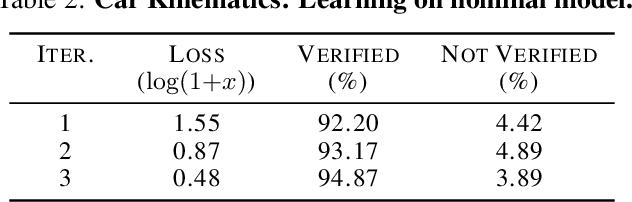
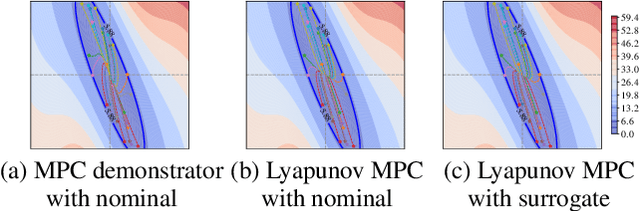
This paper presents Neural Lyapunov MPC, an algorithm to alternately train a Lyapunov neural network and a stabilising constrained Model Predictive Controller (MPC), given a neural network model of the system dynamics. This extends recent works on Lyapunov networks to be able to train solely from expert demonstrations of one-step transitions. The learned Lyapunov network is used as the value function for the MPC in order to guarantee stability and extend the stable region. Formal results are presented on the existence of a set of MPC parameters, such as discount factors, that guarantees stability with a horizon as short as one. Robustness margins are also discussed and existing performance bounds on value function MPC are extended to the case of imperfect models. The approach is tested on unstable non-linear continuous control tasks with hard constraints. Results demonstrate that, when a neural network trained on short sequences is used for predictions, a one-step horizon Neural Lyapunov MPC can successfully reproduce the expert behaviour and significantly outperform longer horizon MPCs.

Safe Interactive Model-Based Learning

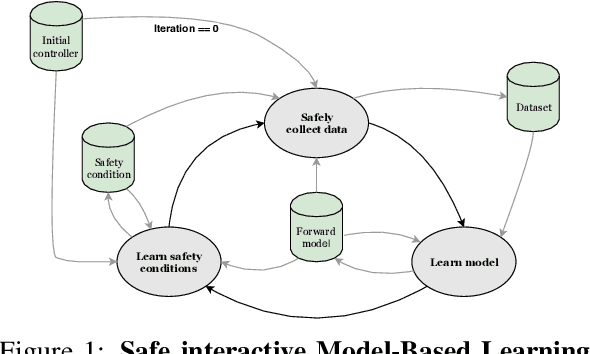
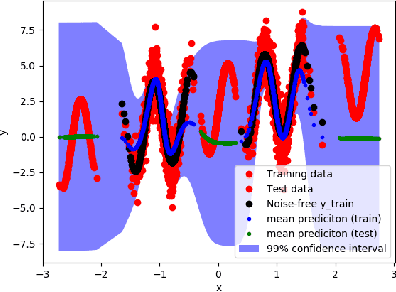
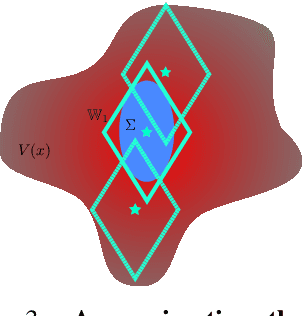
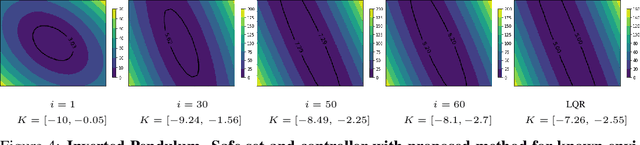
Control applications present hard operational constraints. A violation of these can result in unsafe behavior. This paper introduces Safe Interactive Model Based Learning (SiMBL), a framework to refine an existing controller and a system model while operating on the real environment. SiMBL is composed of the following trainable components: a Lyapunov function, which determines a safe set; a safe control policy; and a Bayesian RNN forward model. A min-max control framework, based on alternate minimisation and backpropagation through the forward model, is used for the offline computation of the controller and the safe set. Safety is formally verified a-posteriori with a probabilistic method that utilizes the Noise Contrastive Priors (NPC) idea to build a Bayesian RNN forward model with an additive state uncertainty estimate which is large outside the training data distribution. Iterative refinement of the model and the safe set is achieved thanks to a novel loss that conditions the uncertainty estimates of the new model to be close to the current one. The learned safe set and model can also be used for safe exploration, i.e., to collect data within the safe invariant set, for which a simple one-step MPC is proposed. The single components are tested on the simulation of an inverted pendulum with limited torque and stability region, showing that iteratively adding more data can improve the model, the controller and the size of the safe region.

Accelerating Neural ODEs with Spectral Elements

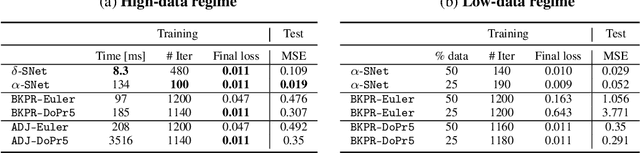
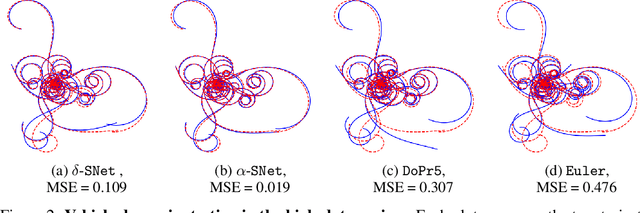
This paper proposes the use of spectral element methods \citep{canuto_spectral_1988} for fast and accurate training of Neural Ordinary Differential Equations (ODE-Nets; \citealp{Chen2018NeuralOD}). This is achieved by expressing their dynamics as truncated series of Legendre polynomials. The series coefficients, as well as the network weights, are computed by minimizing the weighted sum of the loss function and the violation of the ODE-Net dynamics. The problem is solved by coordinate descent that alternately minimizes, with respect to the coefficients and the weights, two unconstrained sub-problems using standard backpropagation and gradient methods. The resulting optimization scheme is fully time-parallel and results in a low memory footprint. Experimental comparison to standard methods, such as backpropagation through explicit solvers and the adjoint technique \citep{Chen2018NeuralOD}, on training surrogate models of small and medium-scale dynamical systems shows that it is at least one order of magnitude faster at reaching a comparable value of the loss function. The corresponding testing MSE is one order of magnitude smaller as well, suggesting generalization capabilities increase.

Smart energy models for atomistic simulations using a DFT-driven multifidelity approach

The reliability of atomistic simulations depends on the quality of the underlying energy models providing the source of physical information, for instance for the calculation of migration barriers in atomistic Kinetic Monte Carlo simulations. Accurate (high-fidelity) methods are often available, but since they are usually computationally expensive, they must be replaced by less accurate (low-fidelity) models that introduce some degrees of approximation. Machine-learning techniques such as artificial neural networks are usually employed to work around this limitation and extract the needed parameters from large databases of high-fidelity data, but the latter are often computationally expensive to produce. This work introduces an alternative method based on the multifidelity approach, where correlations between high-fidelity and low-fidelity outputs are exploited to make an educated guess of the high-fidelity outcome based only on quick low-fidelity estimations, hence without the need of running full expensive high-fidelity calculations. With respect to neural networks, this approach is expected to require less training data because of the lower amount of fitting parameters involved. The method is tested on the prediction of ab initio formation and migration energies of vacancy diffusion in iron-copper alloys, and compared with the neural networks trained on the same database.