Seyed Sina Mirrazavi Salehian
Neural Lyapunov Model Predictive Control
Feb 21, 2020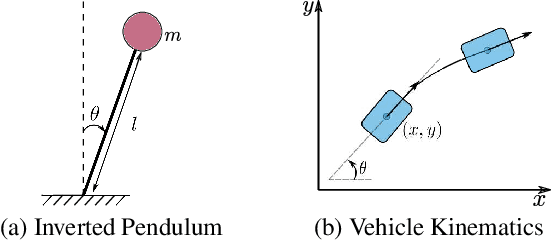

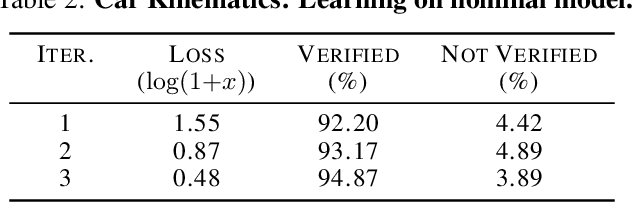
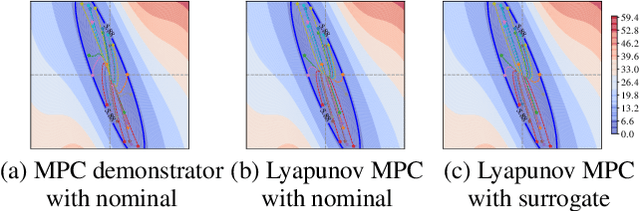
Abstract:This paper presents Neural Lyapunov MPC, an algorithm to alternately train a Lyapunov neural network and a stabilising constrained Model Predictive Controller (MPC), given a neural network model of the system dynamics. This extends recent works on Lyapunov networks to be able to train solely from expert demonstrations of one-step transitions. The learned Lyapunov network is used as the value function for the MPC in order to guarantee stability and extend the stable region. Formal results are presented on the existence of a set of MPC parameters, such as discount factors, that guarantees stability with a horizon as short as one. Robustness margins are also discussed and existing performance bounds on value function MPC are extended to the case of imperfect models. The approach is tested on unstable non-linear continuous control tasks with hard constraints. Results demonstrate that, when a neural network trained on short sequences is used for predictions, a one-step horizon Neural Lyapunov MPC can successfully reproduce the expert behaviour and significantly outperform longer horizon MPCs.
Safe Interactive Model-Based Learning
Nov 18, 2019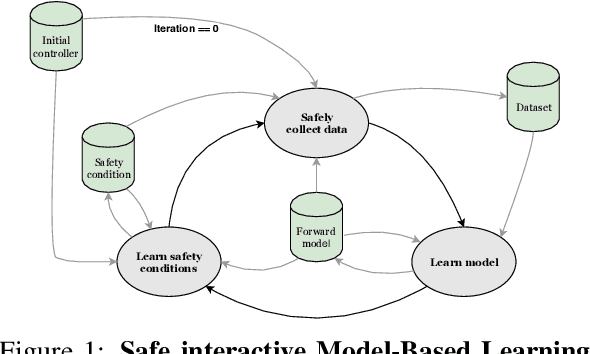
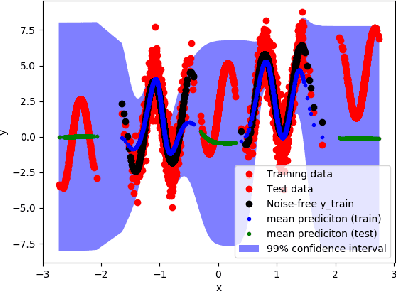
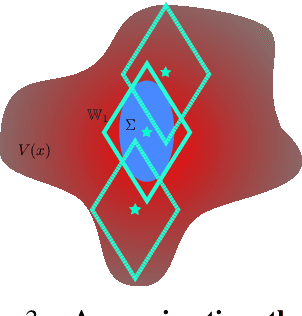
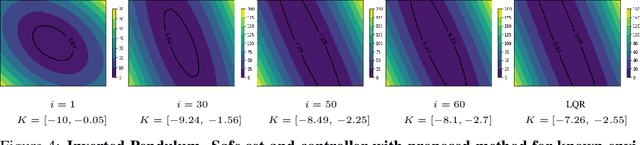
Abstract:Control applications present hard operational constraints. A violation of these can result in unsafe behavior. This paper introduces Safe Interactive Model Based Learning (SiMBL), a framework to refine an existing controller and a system model while operating on the real environment. SiMBL is composed of the following trainable components: a Lyapunov function, which determines a safe set; a safe control policy; and a Bayesian RNN forward model. A min-max control framework, based on alternate minimisation and backpropagation through the forward model, is used for the offline computation of the controller and the safe set. Safety is formally verified a-posteriori with a probabilistic method that utilizes the Noise Contrastive Priors (NPC) idea to build a Bayesian RNN forward model with an additive state uncertainty estimate which is large outside the training data distribution. Iterative refinement of the model and the safe set is achieved thanks to a novel loss that conditions the uncertainty estimates of the new model to be close to the current one. The learned safe set and model can also be used for safe exploration, i.e., to collect data within the safe invariant set, for which a simple one-step MPC is proposed. The single components are tested on the simulation of an inverted pendulum with limited torque and stability region, showing that iteratively adding more data can improve the model, the controller and the size of the safe region.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge