Parallel Trust-Region Approaches in Neural Network Training: Beyond Traditional Methods

We propose to train neural networks (NNs) using a novel variant of the ``Additively Preconditioned Trust-region Strategy'' (APTS). The proposed method is based on a parallelizable additive domain decomposition approach applied to the neural network's parameters. Built upon the TR framework, the APTS method ensures global convergence towards a minimizer. Moreover, it eliminates the need for computationally expensive hyper-parameter tuning, as the TR algorithm automatically determines the step size in each iteration. We demonstrate the capabilities, strengths, and limitations of the proposed APTS training method by performing a series of numerical experiments. The presented numerical study includes a comparison with widely used training methods such as SGD, Adam, LBFGS, and the standard TR method.

Shape of my heart: Cardiac models through learned signed distance functions

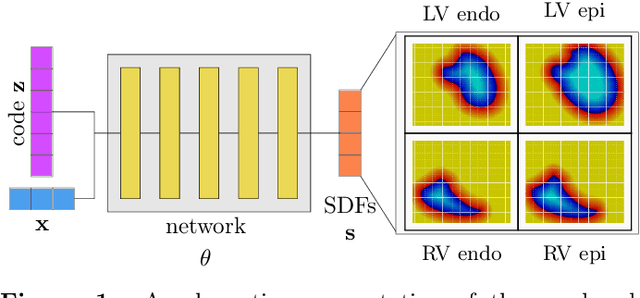
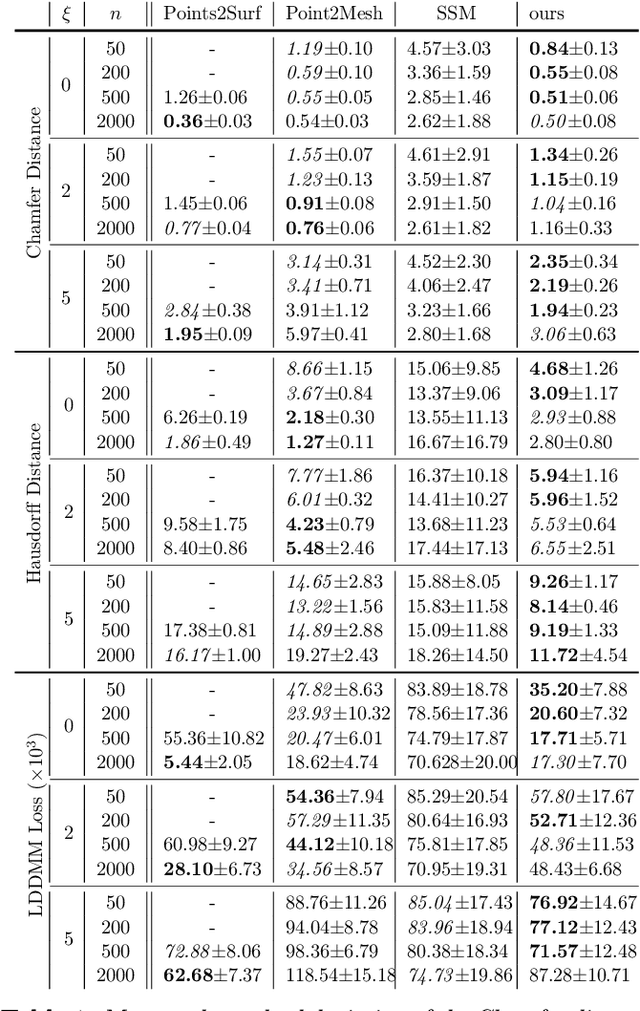
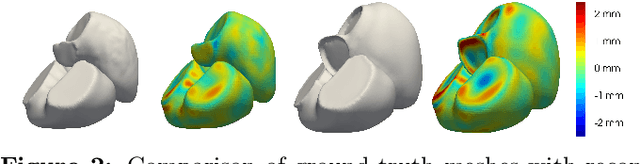
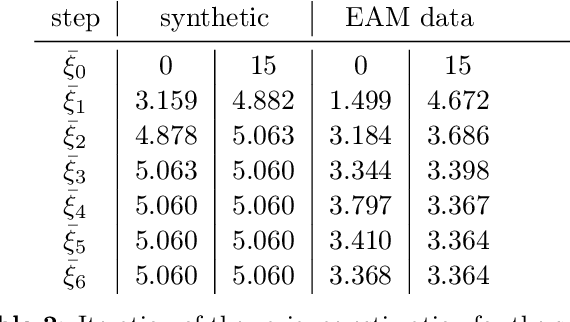
The efficient construction of an anatomical model is one of the major challenges of patient-specific in-silico models of the human heart. Current methods frequently rely on linear statistical models, allowing no advanced topological changes, or requiring medical image segmentation followed by a meshing pipeline, which strongly depends on image resolution, quality, and modality. These approaches are therefore limited in their transferability to other imaging domains. In this work, the cardiac shape is reconstructed by means of three-dimensional deep signed distance functions with Lipschitz regularity. For this purpose, the shapes of cardiac MRI reconstructions are learned from public databases to model the spatial relation of multiple chambers in Cartesian space. We demonstrate that this approach is also capable of reconstructing anatomical models from partial data, such as point clouds from a single ventricle, or modalities different from the trained MRI, such as electroanatomical mapping, and in addition, allows us to generate new anatomical shapes by randomly sampling latent vectors.

Enhancing training of physics-informed neural networks using domain-decomposition based preconditioning strategies

We propose to enhance the training of physics-informed neural networks (PINNs). To this aim, we introduce nonlinear additive and multiplicative preconditioning strategies for the widely used L-BFGS optimizer. The nonlinear preconditioners are constructed by utilizing the Schwarz domain-decomposition framework, where the parameters of the network are decomposed in a layer-wise manner. Through a series of numerical experiments, we demonstrate that both, additive and multiplicative preconditioners significantly improve the convergence of the standard L-BFGS optimizer, while providing more accurate solutions of the underlying partial differential equations. Moreover, the additive preconditioner is inherently parallel, thus giving rise to a novel approach to model parallelism.

Fast characterization of inducible regions of atrial fibrillation models with multi-fidelity Gaussian process classification

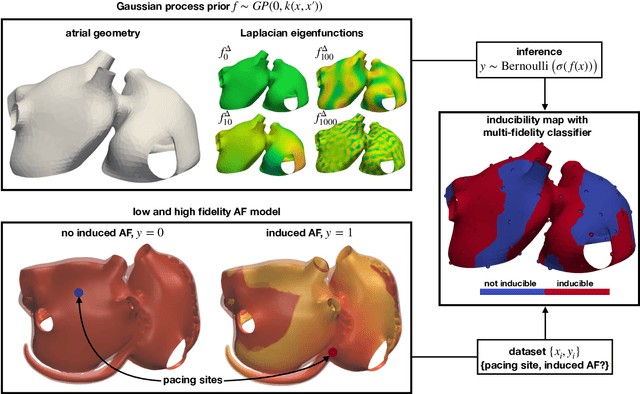
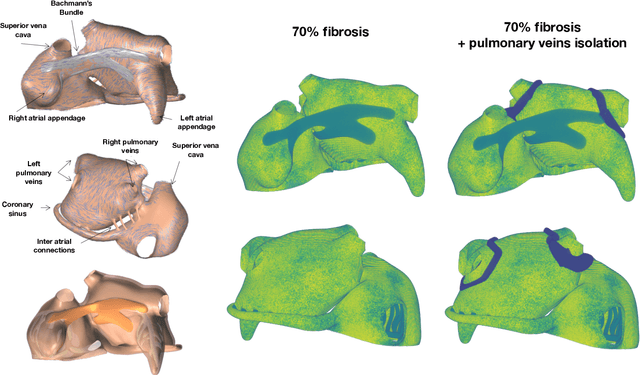
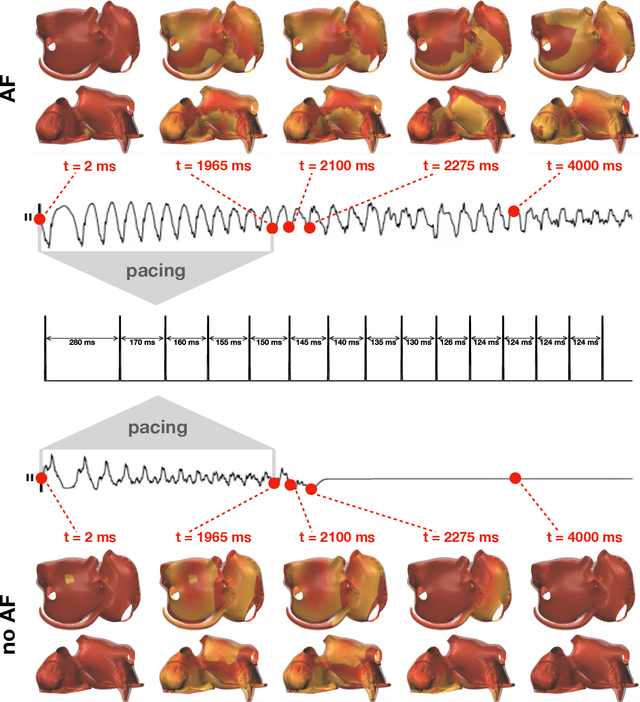
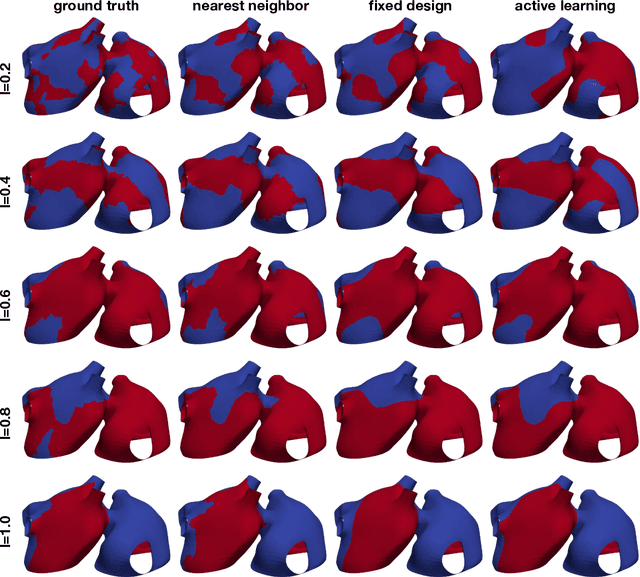
Computational models of atrial fibrillation have successfully been used to predict optimal ablation sites. A critical step to assess the effect of an ablation pattern is to pace the model from different, potentially random, locations to determine whether arrhythmias can be induced in the atria. In this work, we propose to use multi-fidelity Gaussian process classification on Riemannian manifolds to efficiently determine the regions in the atria where arrhythmias are inducible. We build a probabilistic classifier that operates directly on the atrial surface. We take advantage of lower resolution models to explore the atrial surface and combine seamlessly with high-resolution models to identify regions of inducibility. When trained with 40 samples, our multi-fidelity classifier shows a balanced accuracy that is 10% higher than a nearest neighbor classifier used as a baseline atrial fibrillation model, and 9% higher in presence of atrial fibrillation with ablations. We hope that this new technique will allow faster and more precise clinical applications of computational models for atrial fibrillation.

Construction of Grid Operators for Multilevel Solvers: a Neural Network Approach

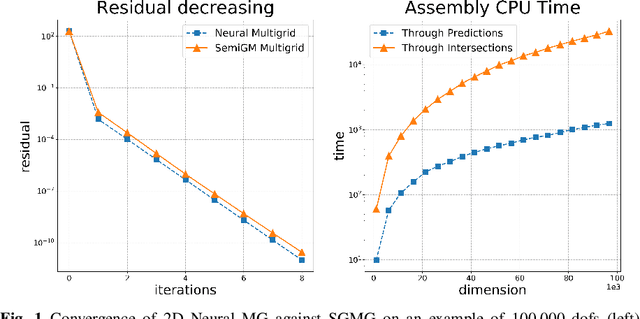
In this paper, we investigate the combination of multigrid methods and neural networks, starting from a Finite Element discretization of an elliptic PDE. Multigrid methods use interpolation operators to transfer information between different levels of approximation. These operators are crucial for fast convergence of multigrid, but they are generally unknown. We propose Deep Neural Network models for learning interpolation operators and we build a multilevel hierarchy based on the output of the network. We investigate the accuracy of the interpolation operator predicted by the Neural Network, testing it with different network architectures. This Neural Network approach for the construction of grid operators can then be extended for an automatic definition of multilevel solvers, allowing a portable solution in scientific computing

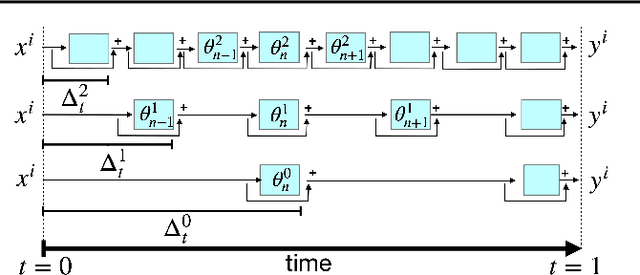
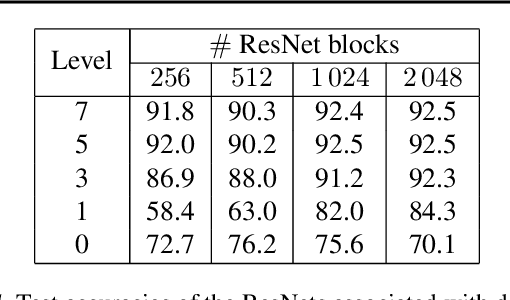
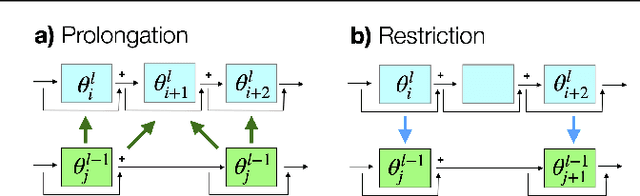
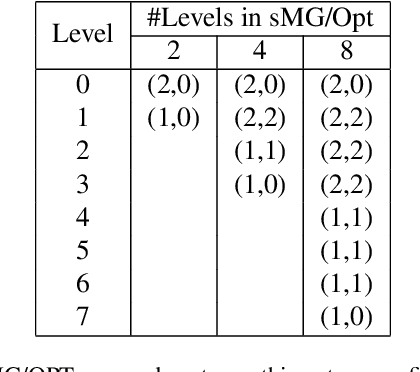
Training of deep residual networks with stochastic MG/OPT

We train deep residual networks with a stochastic variant of the nonlinear multigrid method MG/OPT. To build the multilevel hierarchy, we use the dynamical systems viewpoint specific to residual networks. We report significant speed-ups and additional robustness for training MNIST on deep residual networks. Our numerical experiments also indicate that multilevel training can be used as a pruning technique, as many of the auxiliary networks have accuracies comparable to the original network.

Globally Convergent Multilevel Training of Deep Residual Networks

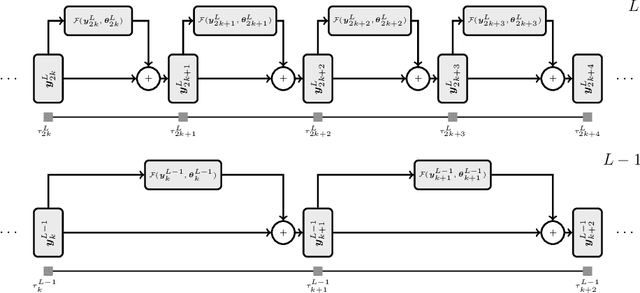
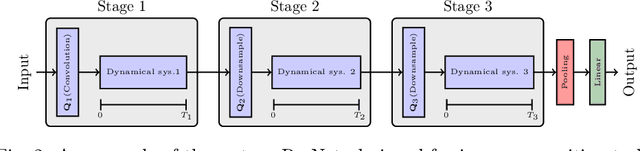
We propose a globally convergent multilevel training method for deep residual networks (ResNets). The devised method can be seen as a novel variant of the recursive multilevel trust-region (RMTR) method, which operates in hybrid (stochastic-deterministic) settings by adaptively adjusting mini-batch sizes during the training. The multilevel hierarchy and the transfer operators are constructed by exploiting a dynamical system's viewpoint, which interprets forward propagation through the ResNet as a forward Euler discretization of an initial value problem. In contrast to traditional training approaches, our novel RMTR method also incorporates curvature information on all levels of the multilevel hierarchy by means of the limited-memory SR1 method. The overall performance and the convergence properties of our multilevel training method are numerically investigated using examples from the field of classification and regression.

Learning atrial fiber orientations and conductivity tensors from intracardiac maps using physics-informed neural networks

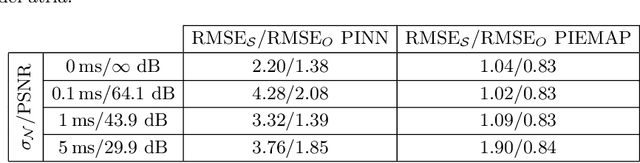
Electroanatomical maps are a key tool in the diagnosis and treatment of atrial fibrillation. Current approaches focus on the activation times recorded. However, more information can be extracted from the available data. The fibers in cardiac tissue conduct the electrical wave faster, and their direction could be inferred from activation times. In this work, we employ a recently developed approach, called physics informed neural networks, to learn the fiber orientations from electroanatomical maps, taking into account the physics of the electrical wave propagation. In particular, we train the neural network to weakly satisfy the anisotropic eikonal equation and to predict the measured activation times. We use a local basis for the anisotropic conductivity tensor, which encodes the fiber orientation. The methodology is tested both in a synthetic example and for patient data. Our approach shows good agreement in both cases and it outperforms a state of the art method in the patient data. The results show a first step towards learning the fiber orientations from electroanatomical maps with physics-informed neural networks.

A Multilevel Approach to Training

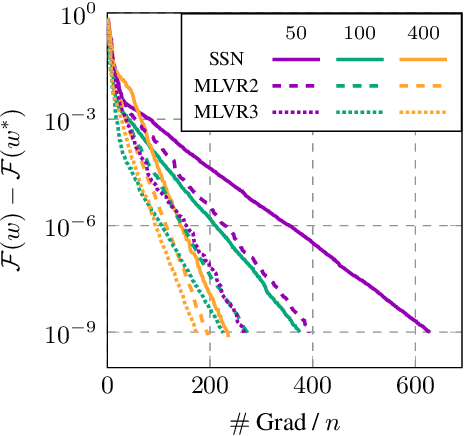
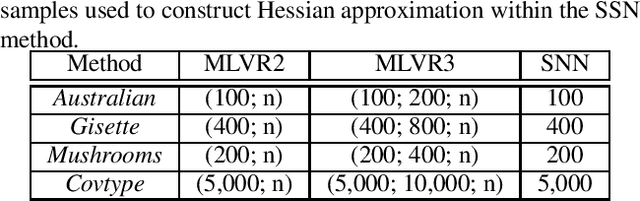
We propose a novel training method based on nonlinear multilevel minimization techniques, commonly used for solving discretized large scale partial differential equations. Our multilevel training method constructs a multilevel hierarchy by reducing the number of samples. The training of the original model is then enhanced by internally training surrogate models constructed with fewer samples. We construct the surrogate models using first-order consistency approach. This gives rise to surrogate models, whose gradients are stochastic estimators of the full gradient, but with reduced variance compared to standard stochastic gradient estimators. We illustrate the convergence behavior of the proposed multilevel method to machine learning applications based on logistic regression. A comparison with subsampled Newton's and variance reduction methods demonstrate the efficiency of our multilevel method.