Vanessa Braglia
A Multilevel Approach to Training
Jun 28, 2020

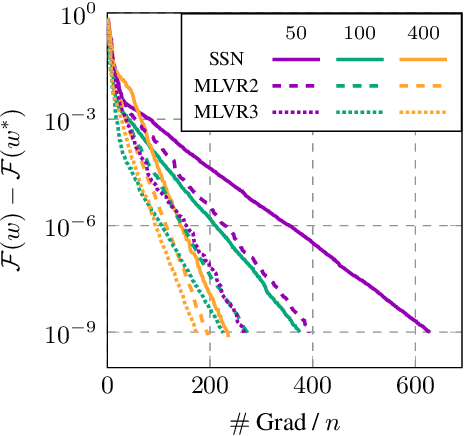
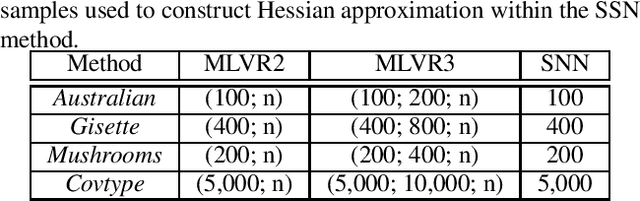
Abstract:We propose a novel training method based on nonlinear multilevel minimization techniques, commonly used for solving discretized large scale partial differential equations. Our multilevel training method constructs a multilevel hierarchy by reducing the number of samples. The training of the original model is then enhanced by internally training surrogate models constructed with fewer samples. We construct the surrogate models using first-order consistency approach. This gives rise to surrogate models, whose gradients are stochastic estimators of the full gradient, but with reduced variance compared to standard stochastic gradient estimators. We illustrate the convergence behavior of the proposed multilevel method to machine learning applications based on logistic regression. A comparison with subsampled Newton's and variance reduction methods demonstrate the efficiency of our multilevel method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge