Two-level overlapping additive Schwarz preconditioner for training scientific machine learning applications

We introduce a novel two-level overlapping additive Schwarz preconditioner for accelerating the training of scientific machine learning applications. The design of the proposed preconditioner is motivated by the nonlinear two-level overlapping additive Schwarz preconditioner. The neural network parameters are decomposed into groups (subdomains) with overlapping regions. In addition, the network's feed-forward structure is indirectly imposed through a novel subdomain-wise synchronization strategy and a coarse-level training step. Through a series of numerical experiments, which consider physics-informed neural networks and operator learning approaches, we demonstrate that the proposed two-level preconditioner significantly speeds up the convergence of the standard (LBFGS) optimizer while also yielding more accurate machine learning models. Moreover, the devised preconditioner is designed to take advantage of model-parallel computations, which can further reduce the training time.

Parallel Trust-Region Approaches in Neural Network Training: Beyond Traditional Methods

We propose to train neural networks (NNs) using a novel variant of the ``Additively Preconditioned Trust-region Strategy'' (APTS). The proposed method is based on a parallelizable additive domain decomposition approach applied to the neural network's parameters. Built upon the TR framework, the APTS method ensures global convergence towards a minimizer. Moreover, it eliminates the need for computationally expensive hyper-parameter tuning, as the TR algorithm automatically determines the step size in each iteration. We demonstrate the capabilities, strengths, and limitations of the proposed APTS training method by performing a series of numerical experiments. The presented numerical study includes a comparison with widely used training methods such as SGD, Adam, LBFGS, and the standard TR method.

Enhancing training of physics-informed neural networks using domain-decomposition based preconditioning strategies

We propose to enhance the training of physics-informed neural networks (PINNs). To this aim, we introduce nonlinear additive and multiplicative preconditioning strategies for the widely used L-BFGS optimizer. The nonlinear preconditioners are constructed by utilizing the Schwarz domain-decomposition framework, where the parameters of the network are decomposed in a layer-wise manner. Through a series of numerical experiments, we demonstrate that both, additive and multiplicative preconditioners significantly improve the convergence of the standard L-BFGS optimizer, while providing more accurate solutions of the underlying partial differential equations. Moreover, the additive preconditioner is inherently parallel, thus giving rise to a novel approach to model parallelism.

Globally Convergent Multilevel Training of Deep Residual Networks

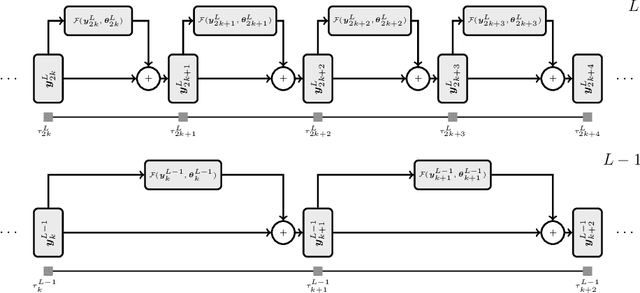
We propose a globally convergent multilevel training method for deep residual networks (ResNets). The devised method can be seen as a novel variant of the recursive multilevel trust-region (RMTR) method, which operates in hybrid (stochastic-deterministic) settings by adaptively adjusting mini-batch sizes during the training. The multilevel hierarchy and the transfer operators are constructed by exploiting a dynamical system's viewpoint, which interprets forward propagation through the ResNet as a forward Euler discretization of an initial value problem. In contrast to traditional training approaches, our novel RMTR method also incorporates curvature information on all levels of the multilevel hierarchy by means of the limited-memory SR1 method. The overall performance and the convergence properties of our multilevel training method are numerically investigated using examples from the field of classification and regression.

A Multilevel Approach to Training

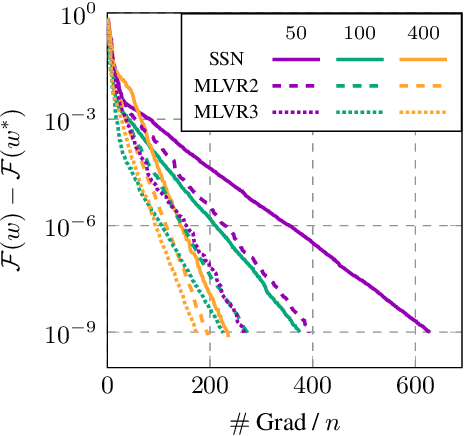
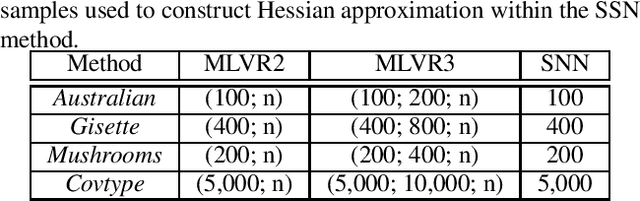
We propose a novel training method based on nonlinear multilevel minimization techniques, commonly used for solving discretized large scale partial differential equations. Our multilevel training method constructs a multilevel hierarchy by reducing the number of samples. The training of the original model is then enhanced by internally training surrogate models constructed with fewer samples. We construct the surrogate models using first-order consistency approach. This gives rise to surrogate models, whose gradients are stochastic estimators of the full gradient, but with reduced variance compared to standard stochastic gradient estimators. We illustrate the convergence behavior of the proposed multilevel method to machine learning applications based on logistic regression. A comparison with subsampled Newton's and variance reduction methods demonstrate the efficiency of our multilevel method.

Multilevel Minimization for Deep Residual Networks

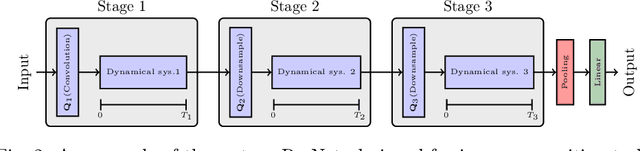
We present a new multilevel minimization framework for the training of deep residual networks (ResNets), which has the potential to significantly reduce training time and effort. Our framework is based on the dynamical system's viewpoint, which formulates a ResNet as the discretization of an initial value problem. The training process is then formulated as a time-dependent optimal control problem, which we discretize using different time-discretization parameters, eventually generating multilevel-hierarchy of auxiliary networks with different resolutions. The training of the original ResNet is then enhanced by training the auxiliary networks with reduced resolutions. By design, our framework is conveniently independent of the choice of the training strategy chosen on each level of the multilevel hierarchy. By means of numerical examples, we analyze the convergence behavior of the proposed method and demonstrate its robustness. For our examples we employ a multilevel gradient-based methods. Comparisons with standard single level methods show a speedup of more than factor three while achieving the same validation accuracy.