Finite element-based space-time total variation-type regularization of the inverse problem in electrocardiographic imaging

Reconstructing cardiac electrical activity from body surface electric potential measurements results in the severely ill-posed inverse problem in electrocardiography. Many different regularization approaches have been proposed to improve numerical results and provide unique results. This work presents a novel approach for reconstructing the epicardial potential from body surface potential maps based on a space-time total variation-type regularization using finite elements, where a first-order primal-dual algorithm solves the underlying convex optimization problem. In several numerical experiments, the superior performance of this method and the benefit of space-time regularization for the reconstruction of epicardial potential on two-dimensional torso data and a three-dimensional rabbit heart compared to state-of-the-art methods are demonstrated.

Gadolinium dose reduction for brain MRI using conditional deep learning

Recently, deep learning (DL)-based methods have been proposed for the computational reduction of gadolinium-based contrast agents (GBCAs) to mitigate adverse side effects while preserving diagnostic value. Currently, the two main challenges for these approaches are the accurate prediction of contrast enhancement and the synthesis of realistic images. In this work, we address both challenges by utilizing the contrast signal encoded in the subtraction images of pre-contrast and post-contrast image pairs. To avoid the synthesis of any noise or artifacts and solely focus on contrast signal extraction and enhancement from low-dose subtraction images, we train our DL model using noise-free standard-dose subtraction images as targets. As a result, our model predicts the contrast enhancement signal only; thereby enabling synthesization of images beyond the standard dose. Furthermore, we adapt the embedding idea of recent diffusion-based models to condition our model on physical parameters affecting the contrast enhancement behavior. We demonstrate the effectiveness of our approach on synthetic and real datasets using various scanners, field strengths, and contrast agents.

Shape of my heart: Cardiac models through learned signed distance functions

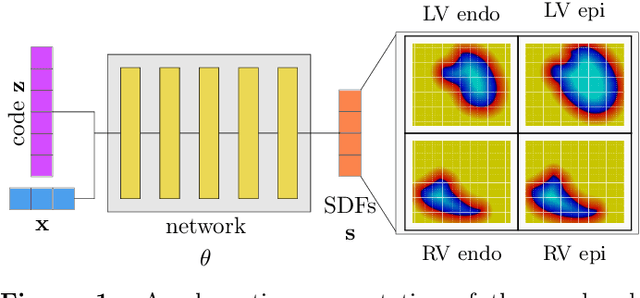
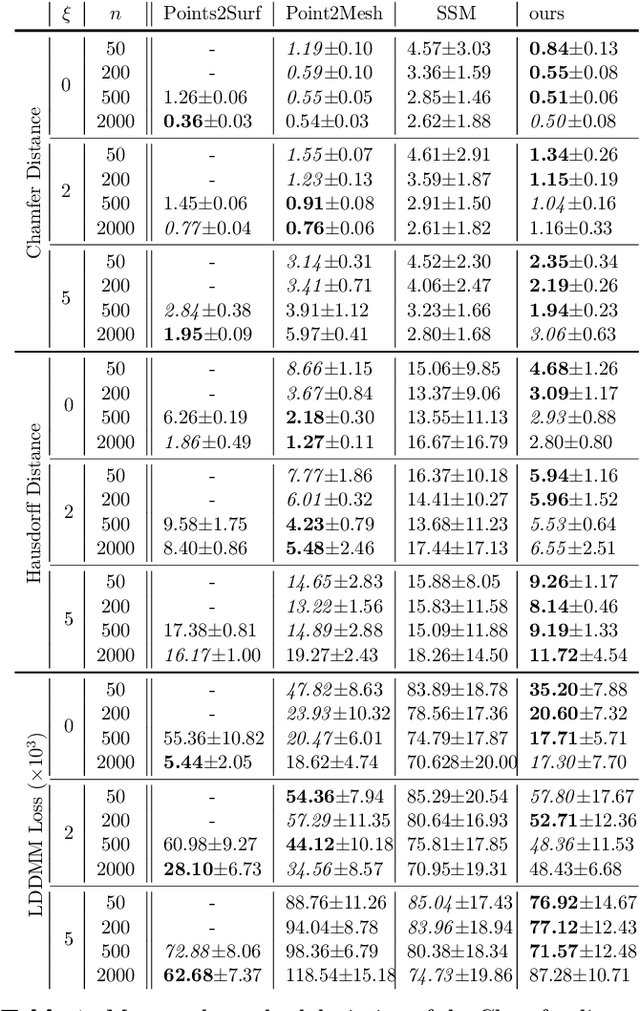
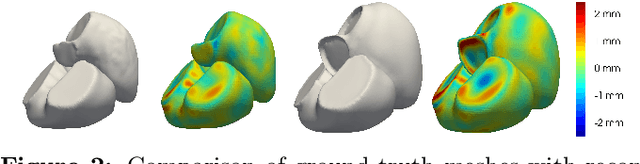
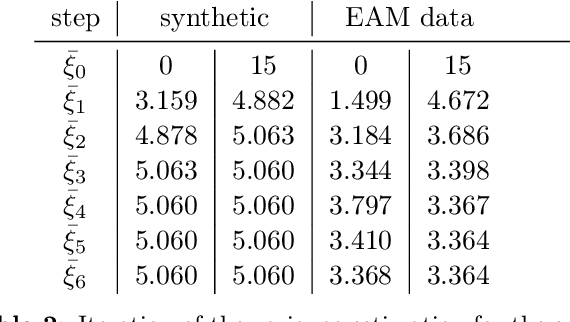
The efficient construction of an anatomical model is one of the major challenges of patient-specific in-silico models of the human heart. Current methods frequently rely on linear statistical models, allowing no advanced topological changes, or requiring medical image segmentation followed by a meshing pipeline, which strongly depends on image resolution, quality, and modality. These approaches are therefore limited in their transferability to other imaging domains. In this work, the cardiac shape is reconstructed by means of three-dimensional deep signed distance functions with Lipschitz regularity. For this purpose, the shapes of cardiac MRI reconstructions are learned from public databases to model the spatial relation of multiple chambers in Cartesian space. We demonstrate that this approach is also capable of reconstructing anatomical models from partial data, such as point clouds from a single ventricle, or modalities different from the trained MRI, such as electroanatomical mapping, and in addition, allows us to generate new anatomical shapes by randomly sampling latent vectors.

Digital twinning of cardiac electrophysiology models from the surface ECG: a geodesic backpropagation approach

The eikonal equation has become an indispensable tool for modeling cardiac electrical activation accurately and efficiently. In principle, by matching clinically recorded and eikonal-based electrocardiograms (ECGs), it is possible to build patient-specific models of cardiac electrophysiology in a purely non-invasive manner. Nonetheless, the fitting procedure remains a challenging task. The present study introduces a novel method, Geodesic-BP, to solve the inverse eikonal problem. Geodesic-BP is well-suited for GPU-accelerated machine learning frameworks, allowing us to optimize the parameters of the eikonal equation to reproduce a given ECG. We show that Geodesic-BP can reconstruct a simulated cardiac activation with high accuracy in a synthetic test case, even in the presence of modeling inaccuracies. Furthermore, we apply our algorithm to a publicly available dataset of a rabbit model, with very positive results. Given the future shift towards personalized medicine, Geodesic-BP has the potential to help in future functionalizations of cardiac models meeting clinical time constraints while maintaining the physiological accuracy of state-of-the-art cardiac models.

Faithful Synthesis of Low-dose Contrast-enhanced Brain MRI Scans using Noise-preserving Conditional GANs

Today Gadolinium-based contrast agents (GBCA) are indispensable in Magnetic Resonance Imaging (MRI) for diagnosing various diseases. However, GBCAs are expensive and may accumulate in patients with potential side effects, thus dose-reduction is recommended. Still, it is unclear to which extent the GBCA dose can be reduced while preserving the diagnostic value -- especially in pathological regions. To address this issue, we collected brain MRI scans at numerous non-standard GBCA dosages and developed a conditional GAN model for synthesizing corresponding images at fractional dose levels. Along with the adversarial loss, we advocate a novel content loss function based on the Wasserstein distance of locally paired patch statistics for the faithful preservation of noise. Our numerical experiments show that conditional GANs are suitable for generating images at different GBCA dose levels and can be used to augment datasets for virtual contrast models. Moreover, our model can be transferred to openly available datasets such as BraTS, where non-standard GBCA dosage images do not exist.

Bayesian Uncertainty Estimation of Learned Variational MRI Reconstruction

Recent deep learning approaches focus on improving quantitative scores of dedicated benchmarks, and therefore only reduce the observation-related (aleatoric) uncertainty. However, the model-immanent (epistemic) uncertainty is less frequently systematically analyzed. In this work, we introduce a Bayesian variational framework to quantify the epistemic uncertainty. To this end, we solve the linear inverse problem of undersampled MRI reconstruction in a variational setting. The associated energy functional is composed of a data fidelity term and the total deep variation (TDV) as a learned parametric regularizer. To estimate the epistemic uncertainty we draw the parameters of the TDV regularizer from a multivariate Gaussian distribution, whose mean and covariance matrix are learned in a stochastic optimal control problem. In several numerical experiments, we demonstrate that our approach yields competitive results for undersampled MRI reconstruction. Moreover, we can accurately quantify the pixelwise epistemic uncertainty, which can serve radiologists as an additional resource to visualize reconstruction reliability.

Shared Prior Learning of Energy-Based Models for Image Reconstruction

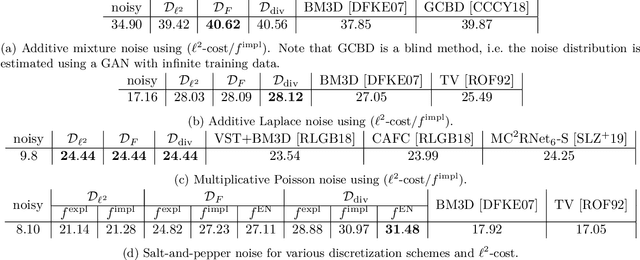
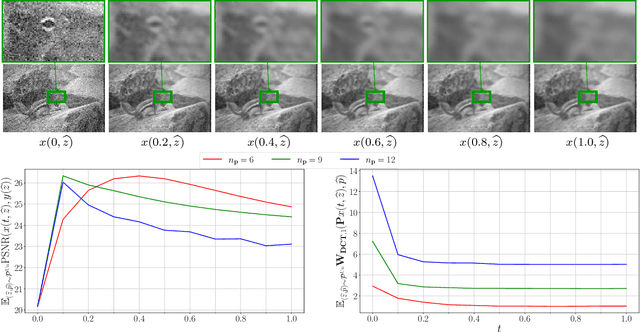
We propose a novel learning-based framework for image reconstruction particularly designed for training without ground truth data, which has three major building blocks: energy-based learning, a patch-based Wasserstein loss functional, and shared prior learning. In energy-based learning, the parameters of an energy functional composed of a learned data fidelity term and a data-driven regularizer are computed in a mean-field optimal control problem. In the absence of ground truth data, we change the loss functional to a patch-based Wasserstein functional, in which local statistics of the output images are compared to uncorrupted reference patches. Finally, in shared prior learning, both aforementioned optimal control problems are optimized simultaneously with shared learned parameters of the regularizer to further enhance unsupervised image reconstruction. We derive several time discretization schemes of the gradient flow and verify their consistency in terms of Mosco convergence. In numerous numerical experiments, we demonstrate that the proposed method generates state-of-the-art results for various image reconstruction applications--even if no ground truth images are available for training.

Total Deep Variation: A Stable Regularizer for Inverse Problems

Various problems in computer vision and medical imaging can be cast as inverse problems. A frequent method for solving inverse problems is the variational approach, which amounts to minimizing an energy composed of a data fidelity term and a regularizer. Classically, handcrafted regularizers are used, which are commonly outperformed by state-of-the-art deep learning approaches. In this work, we combine the variational formulation of inverse problems with deep learning by introducing the data-driven general-purpose total deep variation regularizer. In its core, a convolutional neural network extracts local features on multiple scales and in successive blocks. This combination allows for a rigorous mathematical analysis including an optimal control formulation of the training problem in a mean-field setting and a stability analysis with respect to the initial values and the parameters of the regularizer. In addition, we experimentally verify the robustness against adversarial attacks and numerically derive upper bounds for the generalization error. Finally, we achieve state-of-the-art results for numerous imaging tasks.

Total Deep Variation for Linear Inverse Problems

Diverse inverse problems in imaging can be cast as variational problems composed of a task-specific data fidelity term and a regularization term. In this paper, we propose a novel learnable general-purpose regularizer exploiting recent architectural design patterns from deep learning. We cast the learning problem as a discrete sampled optimal control problem, for which we derive the adjoint state equations and an optimality condition. By exploiting the variational structure of our approach, we perform a sensitivity analysis with respect to the learned parameters obtained from different training datasets. Moreover, we carry out a nonlinear eigenfunction analysis, which reveals interesting properties of the learned regularizer. We show state-of-the-art performance for classical image restoration and medical image reconstruction problems.

An Optimal Control Approach to Early Stopping Variational Methods for Image Restoration

We investigate a well-known phenomenon of variational approaches in image processing, where typically the best image quality is achieved when the gradient flow process is stopped before converging to a stationary point. This paradox originates from a tradeoff between optimization and modelling errors of the underlying variational model and holds true even if deep learning methods are used to learn highly expressive regularizers from data. In this paper, we take advantage of this paradox and introduce an optimal stopping time into the gradient flow process, which in turn is learned from data by means of an optimal control approach. As a result, we obtain highly efficient numerical schemes that achieve competitive results for image denoising and image deblurring. A nonlinear spectral analysis of the gradient of the learned regularizer gives enlightening insights about the different regularization properties.