Shared Prior Learning of Energy-Based Models for Image Reconstruction
Paper and Code
Nov 13, 2020

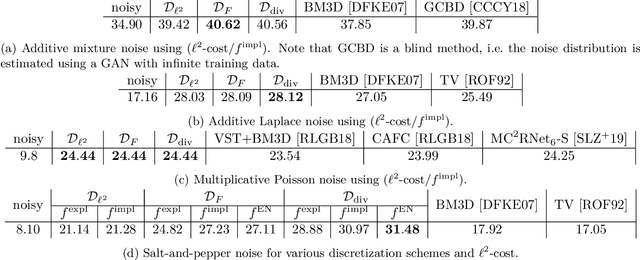
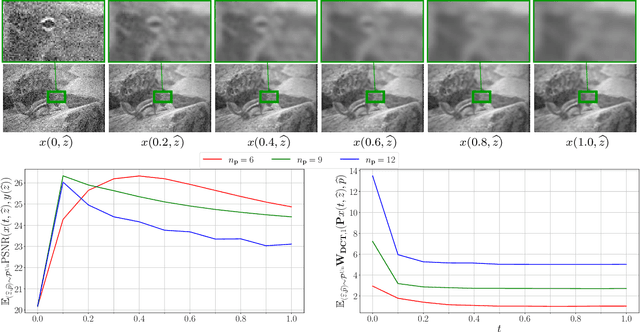
We propose a novel learning-based framework for image reconstruction particularly designed for training without ground truth data, which has three major building blocks: energy-based learning, a patch-based Wasserstein loss functional, and shared prior learning. In energy-based learning, the parameters of an energy functional composed of a learned data fidelity term and a data-driven regularizer are computed in a mean-field optimal control problem. In the absence of ground truth data, we change the loss functional to a patch-based Wasserstein functional, in which local statistics of the output images are compared to uncorrupted reference patches. Finally, in shared prior learning, both aforementioned optimal control problems are optimized simultaneously with shared learned parameters of the regularizer to further enhance unsupervised image reconstruction. We derive several time discretization schemes of the gradient flow and verify their consistency in terms of Mosco convergence. In numerous numerical experiments, we demonstrate that the proposed method generates state-of-the-art results for various image reconstruction applications--even if no ground truth images are available for training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge