Learning Regularization Functionals for Inverse Problems: A Comparative Study

In recent years, a variety of learned regularization frameworks for solving inverse problems in imaging have emerged. These offer flexible modeling together with mathematical insights. The proposed methods differ in their architectural design and training strategies, making direct comparison challenging due to non-modular implementations. We address this gap by collecting and unifying the available code into a common framework. This unified view allows us to systematically compare the approaches and highlight their strengths and limitations, providing valuable insights into their future potential. We also provide concise descriptions of each method, complemented by practical guidelines.

Synthesizing Accurate and Realistic T1-weighted Contrast-Enhanced MR Images using Posterior-Mean Rectified Flow

Contrast-enhanced (CE) T1-weighted MRI is central to neuro-oncologic diagnosis but requires gadolinium-based agents, which add cost and scan time, raise environmental concerns, and may pose risks to patients. In this work, we propose a two-stage Posterior-Mean Rectified Flow (PMRF) pipeline for synthesizing volumetric CE brain MRI from non-contrast inputs. First, a patch-based 3D U-Net predicts the voxel-wise posterior mean (minimizing MSE). Then, this initial estimate is refined by a time-conditioned 3D rectified flow to incorporate realistic textures without compromising structural fidelity. We train this model on a multi-institutional collection of paired pre- and post-contrast T1w volumes (BraTS 2023-2025). On a held-out test set of 360 diverse volumes, our best refined outputs achieve an axial FID of $12.46$ and KID of $0.007$ ($\sim 68.7\%$ lower FID than the posterior mean) while maintaining low volumetric MSE of $0.057$ ($\sim 27\%$ higher than the posterior mean). Qualitative comparisons confirm that our method restores lesion margins and vascular details realistically, effectively navigating the perception-distortion trade-off for clinical deployment.

DEALing with Image Reconstruction: Deep Attentive Least Squares

State-of-the-art image reconstruction often relies on complex, highly parameterized deep architectures. We propose an alternative: a data-driven reconstruction method inspired by the classic Tikhonov regularization. Our approach iteratively refines intermediate reconstructions by solving a sequence of quadratic problems. These updates have two key components: (i) learned filters to extract salient image features, and (ii) an attention mechanism that locally adjusts the penalty of filter responses. Our method achieves performance on par with leading plug-and-play and learned regularizer approaches while offering interpretability, robustness, and convergent behavior. In effect, we bridge traditional regularization and deep learning with a principled reconstruction approach.

Efficient MedSAMs: Segment Anything in Medical Images on Laptop

Promptable segmentation foundation models have emerged as a transformative approach to addressing the diverse needs in medical images, but most existing models require expensive computing, posing a big barrier to their adoption in clinical practice. In this work, we organized the first international competition dedicated to promptable medical image segmentation, featuring a large-scale dataset spanning nine common imaging modalities from over 20 different institutions. The top teams developed lightweight segmentation foundation models and implemented an efficient inference pipeline that substantially reduced computational requirements while maintaining state-of-the-art segmentation accuracy. Moreover, the post-challenge phase advanced the algorithms through the design of performance booster and reproducibility tasks, resulting in improved algorithms and validated reproducibility of the winning solution. Furthermore, the best-performing algorithms have been incorporated into the open-source software with a user-friendly interface to facilitate clinical adoption. The data and code are publicly available to foster the further development of medical image segmentation foundation models and pave the way for impactful real-world applications.

Gadolinium dose reduction for brain MRI using conditional deep learning

Recently, deep learning (DL)-based methods have been proposed for the computational reduction of gadolinium-based contrast agents (GBCAs) to mitigate adverse side effects while preserving diagnostic value. Currently, the two main challenges for these approaches are the accurate prediction of contrast enhancement and the synthesis of realistic images. In this work, we address both challenges by utilizing the contrast signal encoded in the subtraction images of pre-contrast and post-contrast image pairs. To avoid the synthesis of any noise or artifacts and solely focus on contrast signal extraction and enhancement from low-dose subtraction images, we train our DL model using noise-free standard-dose subtraction images as targets. As a result, our model predicts the contrast enhancement signal only; thereby enabling synthesization of images beyond the standard dose. Furthermore, we adapt the embedding idea of recent diffusion-based models to condition our model on physical parameters affecting the contrast enhancement behavior. We demonstrate the effectiveness of our approach on synthetic and real datasets using various scanners, field strengths, and contrast agents.

Product of Gaussian Mixture Diffusion Models

In this work we tackle the problem of estimating the density $ f_X $ of a random variable $ X $ by successive smoothing, such that the smoothed random variable $ Y $ fulfills the diffusion partial differential equation $ (\partial_t - \Delta_1)f_Y(\,\cdot\,, t) = 0 $ with initial condition $ f_Y(\,\cdot\,, 0) = f_X $. We propose a product-of-experts-type model utilizing Gaussian mixture experts and study configurations that admit an analytic expression for $ f_Y (\,\cdot\,, t) $. In particular, with a focus on image processing, we derive conditions for models acting on filter-, wavelet-, and shearlet responses. Our construction naturally allows the model to be trained simultaneously over the entire diffusion horizon using empirical Bayes. We show numerical results for image denoising where our models are competitive while being tractable, interpretable, and having only a small number of learnable parameters. As a byproduct, our models can be used for reliable noise estimation, allowing blind denoising of images corrupted by heteroscedastic noise.

Faithful Synthesis of Low-dose Contrast-enhanced Brain MRI Scans using Noise-preserving Conditional GANs

Today Gadolinium-based contrast agents (GBCA) are indispensable in Magnetic Resonance Imaging (MRI) for diagnosing various diseases. However, GBCAs are expensive and may accumulate in patients with potential side effects, thus dose-reduction is recommended. Still, it is unclear to which extent the GBCA dose can be reduced while preserving the diagnostic value -- especially in pathological regions. To address this issue, we collected brain MRI scans at numerous non-standard GBCA dosages and developed a conditional GAN model for synthesizing corresponding images at fractional dose levels. Along with the adversarial loss, we advocate a novel content loss function based on the Wasserstein distance of locally paired patch statistics for the faithful preservation of noise. Our numerical experiments show that conditional GANs are suitable for generating images at different GBCA dose levels and can be used to augment datasets for virtual contrast models. Moreover, our model can be transferred to openly available datasets such as BraTS, where non-standard GBCA dosage images do not exist.

Learning Gradually Non-convex Image Priors Using Score Matching

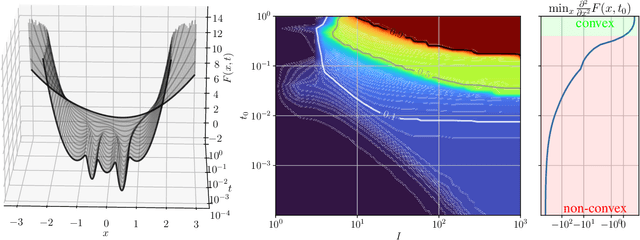
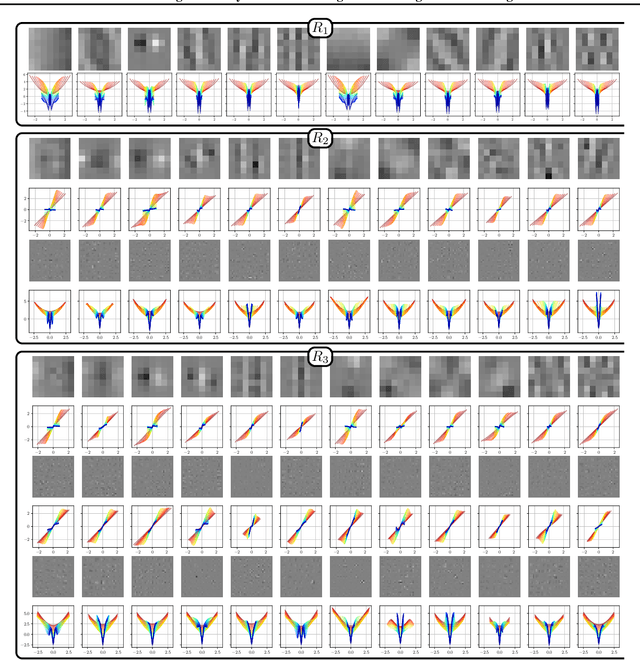
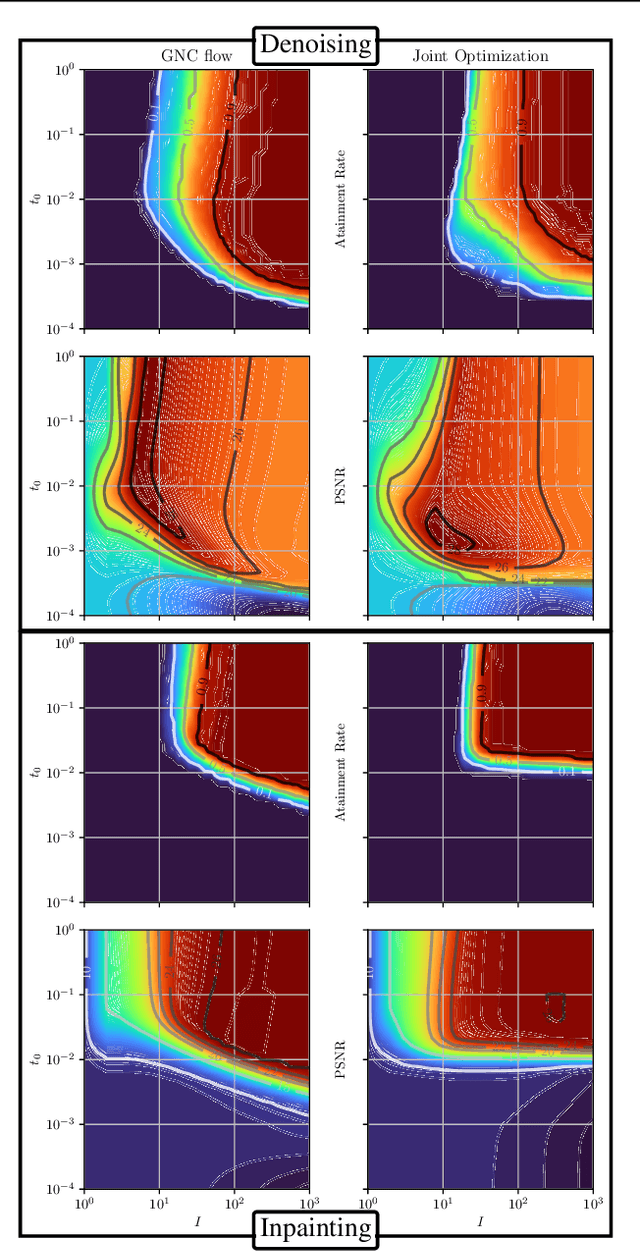
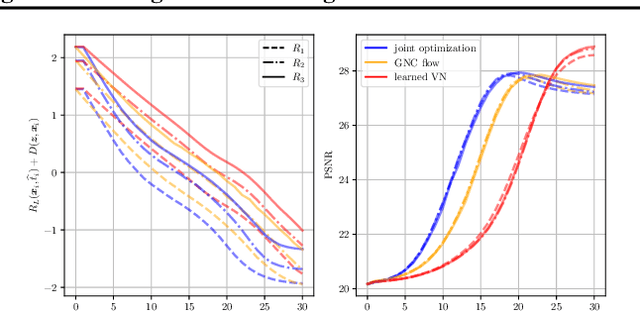
In this paper, we propose a unified framework of denoising score-based models in the context of graduated non-convex energy minimization. We show that for sufficiently large noise variance, the associated negative log density -- the energy -- becomes convex. Consequently, denoising score-based models essentially follow a graduated non-convexity heuristic. We apply this framework to learning generalized Fields of Experts image priors that approximate the joint density of noisy images and their associated variances. These priors can be easily incorporated into existing optimization algorithms for solving inverse problems and naturally implement a fast and robust graduated non-convexity mechanism.

Explicit Diffusion of Gaussian Mixture Model Based Image Priors

In this work we tackle the problem of estimating the density $f_X$ of a random variable $X$ by successive smoothing, such that the smoothed random variable $Y$ fulfills $(\partial_t - \Delta_1)f_Y(\,\cdot\,, t) = 0$, $f_Y(\,\cdot\,, 0) = f_X$. With a focus on image processing, we propose a product/fields of experts model with Gaussian mixture experts that admits an analytic expression for $f_Y (\,\cdot\,, t)$ under an orthogonality constraint on the filters. This construction naturally allows the model to be trained simultaneously over the entire diffusion horizon using empirical Bayes. We show preliminary results on image denoising where our model leads to competitive results while being tractable, interpretable, and having only a small number of learnable parameters. As a byproduct, our model can be used for reliable noise estimation, allowing blind denoising of images corrupted by heteroscedastic noise.

Computed Tomography Reconstruction using Generative Energy-Based Priors

In the past decades, Computed Tomography (CT) has established itself as one of the most important imaging techniques in medicine. Today, the applicability of CT is only limited by the deposited radiation dose, reduction of which manifests in noisy or incomplete measurements. Thus, the need for robust reconstruction algorithms arises. In this work, we learn a parametric regularizer with a global receptive field by maximizing it's likelihood on reference CT data. Due to this unsupervised learning strategy, our trained regularizer truly represents higher-level domain statistics, which we empirically demonstrate by synthesizing CT images. Moreover, this regularizer can easily be applied to different CT reconstruction problems by embedding it in a variational framework, which increases flexibility and interpretability compared to feed-forward learning-based approaches. In addition, the accompanying probabilistic perspective enables experts to explore the full posterior distribution and may quantify uncertainty of the reconstruction approach. We apply the regularizer to limited-angle and few-view CT reconstruction problems, where it outperforms traditional reconstruction algorithms by a large margin.