An Adaptively Inexact Method for Bilevel Learning Using Primal-Dual Style Differentiation

We consider a bilevel learning framework for learning linear operators. In this framework, the learnable parameters are optimized via a loss function that also depends on the minimizer of a convex optimization problem (denoted lower-level problem). We utilize an iterative algorithm called `piggyback' to compute the gradient of the loss and minimizer of the lower-level problem. Given that the lower-level problem is solved numerically, the loss function and thus its gradient can only be computed inexactly. To estimate the accuracy of the computed hypergradient, we derive an a-posteriori error bound, which provides guides for setting the tolerance for the lower-level problem, as well as the piggyback algorithm. To efficiently solve the upper-level optimization, we also propose an adaptive method for choosing a suitable step-size. To illustrate the proposed method, we consider a few learned regularizer problems, such as training an input-convex neural network.

A Primal-dual algorithm for image reconstruction with ICNNs

We address the optimization problem in a data-driven variational reconstruction framework, where the regularizer is parameterized by an input-convex neural network (ICNN). While gradient-based methods are commonly used to solve such problems, they struggle to effectively handle non-smoothness which often leads to slow convergence. Moreover, the nested structure of the neural network complicates the application of standard non-smooth optimization techniques, such as proximal algorithms. To overcome these challenges, we reformulate the problem and eliminate the network's nested structure. By relating this reformulation to epigraphical projections of the activation functions, we transform the problem into a convex optimization problem that can be efficiently solved using a primal-dual algorithm. We also prove that this reformulation is equivalent to the original variational problem. Through experiments on several imaging tasks, we demonstrate that the proposed approach outperforms subgradient methods in terms of both speed and stability.

Deep Tensor CCA for Multi-view Learning

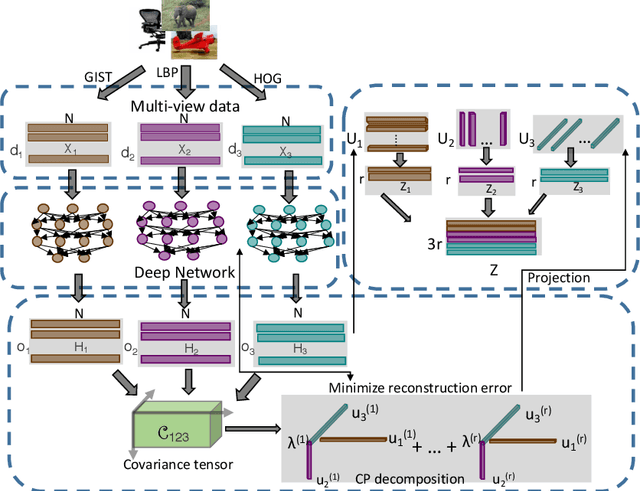
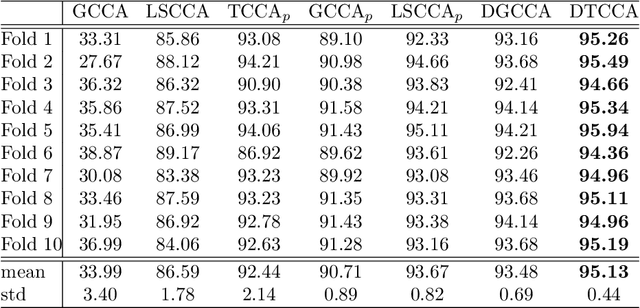
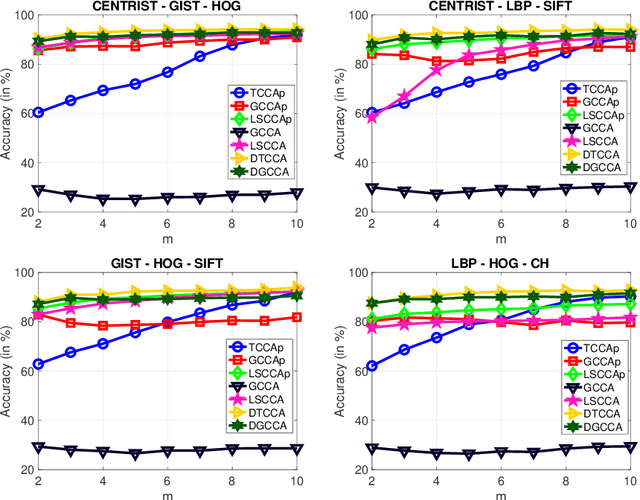
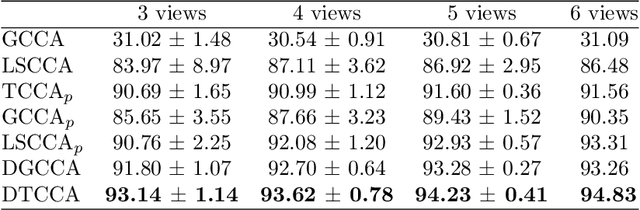
We present Deep Tensor Canonical Correlation Analysis (DTCCA), a method to learn complex nonlinear transformations of multiple views (more than two) of data such that the resulting representations are linearly correlated in high order. The high-order correlation of given multiple views is modeled by covariance tensor, which is different from most CCA formulations relying solely on the pairwise correlations. Parameters of transformations of each view are jointly learned by maximizing the high-order canonical correlation. To solve the resulting problem, we reformulate it as the best sum of rank-1 approximation, which can be efficiently solved by existing tensor decomposition method. DTCCA is a nonlinear extension of tensor CCA (TCCA) via deep networks. The transformations of DTCCA are parametric functions, which are very different from implicit mapping in the form of kernel function. Comparing with kernel TCCA, DTCCA not only can deal with arbitrary dimensions of the input data, but also does not need to maintain the training data for computing representations of any given data point. Hence, DTCCA as a unified model can efficiently overcome the scalable issue of TCCA for either high-dimensional multi-view data or a large amount of views, and it also naturally extends TCCA for learning nonlinear representation. Extensive experiments on three multi-view data sets demonstrate the effectiveness of the proposed method.