Masked Conditional Diffusion Model for Enhancing Deepfake Detection

Recent studies on deepfake detection have achieved promising results when training and testing faces are from the same dataset. However, their results severely degrade when confronted with forged samples that the model has not yet seen during training. In this paper, deepfake data to help detect deepfakes. this paper present we put a new insight into diffusion model-based data augmentation, and propose a Masked Conditional Diffusion Model (MCDM) for enhancing deepfake detection. It generates a variety of forged faces from a masked pristine one, encouraging the deepfake detection model to learn generic and robust representations without overfitting to special artifacts. Extensive experiments demonstrate that forgery images generated with our method are of high quality and helpful to improve the performance of deepfake detection models.

What's in a Prior? Learned Proximal Networks for Inverse Problems

Proximal operators are ubiquitous in inverse problems, commonly appearing as part of algorithmic strategies to regularize problems that are otherwise ill-posed. Modern deep learning models have been brought to bear for these tasks too, as in the framework of plug-and-play or deep unrolling, where they loosely resemble proximal operators. Yet, something essential is lost in employing these purely data-driven approaches: there is no guarantee that a general deep network represents the proximal operator of any function, nor is there any characterization of the function for which the network might provide some approximate proximal. This not only makes guaranteeing convergence of iterative schemes challenging but, more fundamentally, complicates the analysis of what has been learned by these networks about their training data. Herein we provide a framework to develop learned proximal networks (LPN), prove that they provide exact proximal operators for a data-driven nonconvex regularizer, and show how a new training strategy, dubbed proximal matching, provably promotes the recovery of the log-prior of the true data distribution. Such LPN provide general, unsupervised, expressive proximal operators that can be used for general inverse problems with convergence guarantees. We illustrate our results in a series of cases of increasing complexity, demonstrating that these models not only result in state-of-the-art performance, but provide a window into the resulting priors learned from data.

DeepSTI: Towards Tensor Reconstruction using Fewer Orientations in Susceptibility Tensor Imaging

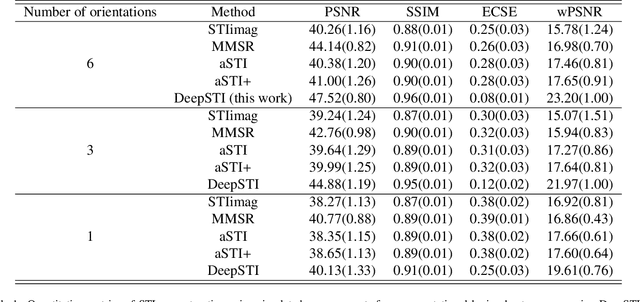
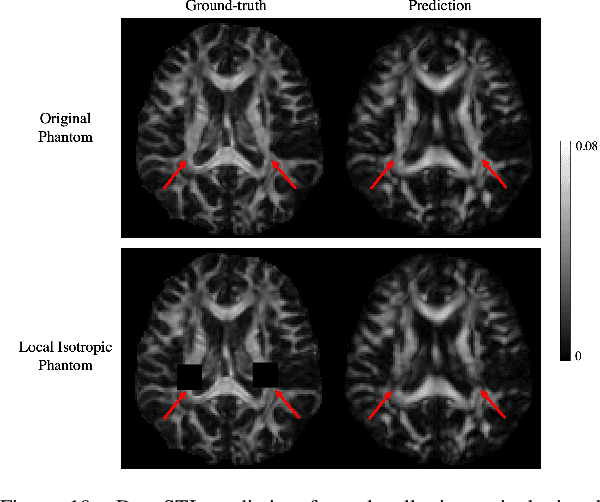
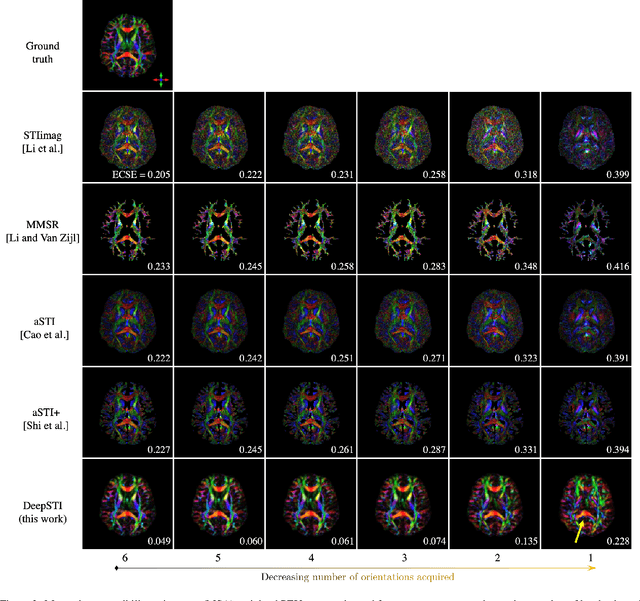
Susceptibility tensor imaging (STI) is an emerging magnetic resonance imaging technique that characterizes the anisotropic tissue magnetic susceptibility with a second-order tensor model. STI has the potential to provide information for both the reconstruction of white matter fiber pathways and detection of myelin changes in the brain at mm resolution or less, which would be of great value for understanding brain structure and function in healthy and diseased brain. However, the application of STI in vivo has been hindered by its cumbersome and time-consuming acquisition requirement of measuring susceptibility induced MR phase changes at multiple (usually more than six) head orientations. This complexity is enhanced by the limitation in head rotation angles due to physical constraints of the head coil. As a result, STI has not yet been widely applied in human studies in vivo. In this work, we tackle these issues by proposing an image reconstruction algorithm for STI that leverages data-driven priors. Our method, called DeepSTI, learns the data prior implicitly via a deep neural network that approximates the proximal operator of a regularizer function for STI. The dipole inversion problem is then solved iteratively using the learned proximal network. Experimental results using both simulation and in vivo human data demonstrate great improvement over state-of-the-art algorithms in terms of the reconstructed tensor image, principal eigenvector maps and tractography results, while allowing for tensor reconstruction with MR phase measured at much less than six different orientations. Notably, promising reconstruction results are achieved by our method from only one orientation in human in vivo, and we demonstrate a potential application of this technique for estimating lesion susceptibility anisotropy in patients with multiple sclerosis.