Sharp analysis of out-of-distribution error for "importance-weighted" estimators in the overparameterized regime

Overparameterized models that achieve zero training error are observed to generalize well on average, but degrade in performance when faced with data that is under-represented in the training sample. In this work, we study an overparameterized Gaussian mixture model imbued with a spurious feature, and sharply analyze the in-distribution and out-of-distribution test error of a cost-sensitive interpolating solution that incorporates "importance weights". Compared to recent work Wang et al. (2021), Behnia et al. (2022), our analysis is sharp with matching upper and lower bounds, and significantly weakens required assumptions on data dimensionality. Our error characterizations also apply to any choice of importance weights and unveil a novel tradeoff between worst-case robustness to distribution shift and average accuracy as a function of the importance weight magnitude.

General Loss Functions Lead to (Approximate) Interpolation in High Dimensions

We provide a unified framework, applicable to a general family of convex losses and across binary and multiclass settings in the overparameterized regime, to approximately characterize the implicit bias of gradient descent in closed form. Specifically, we show that the implicit bias is approximated (but not exactly equal to) the minimum-norm interpolation in high dimensions, which arises from training on the squared loss. In contrast to prior work which was tailored to exponentially-tailed losses and used the intermediate support-vector-machine formulation, our framework directly builds on the primal-dual analysis of Ji and Telgarsky (2021), allowing us to provide new approximate equivalences for general convex losses through a novel sensitivity analysis. Our framework also recovers existing exact equivalence results for exponentially-tailed losses across binary and multiclass settings. Finally, we provide evidence for the tightness of our techniques, which we use to demonstrate the effect of certain loss functions designed for out-of-distribution problems on the closed-form solution.

DeepSTI: Towards Tensor Reconstruction using Fewer Orientations in Susceptibility Tensor Imaging

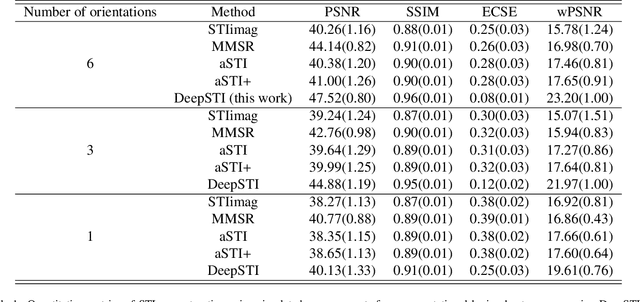
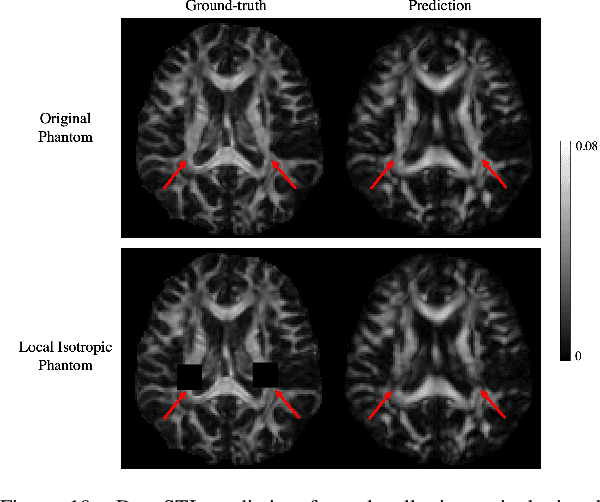
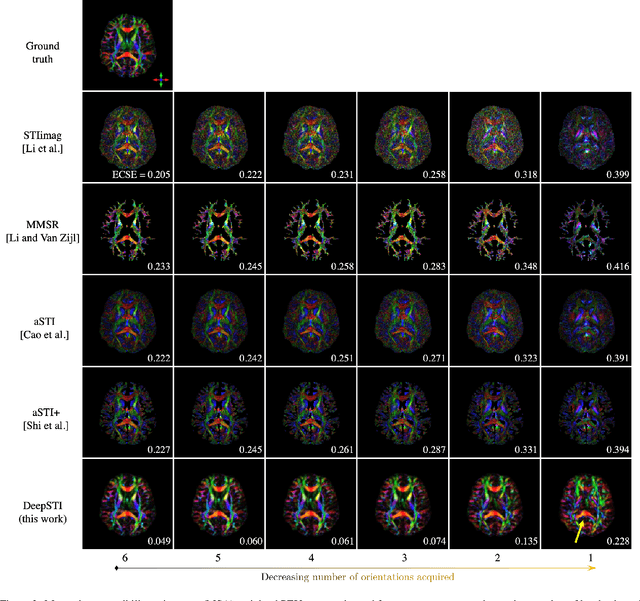
Susceptibility tensor imaging (STI) is an emerging magnetic resonance imaging technique that characterizes the anisotropic tissue magnetic susceptibility with a second-order tensor model. STI has the potential to provide information for both the reconstruction of white matter fiber pathways and detection of myelin changes in the brain at mm resolution or less, which would be of great value for understanding brain structure and function in healthy and diseased brain. However, the application of STI in vivo has been hindered by its cumbersome and time-consuming acquisition requirement of measuring susceptibility induced MR phase changes at multiple (usually more than six) head orientations. This complexity is enhanced by the limitation in head rotation angles due to physical constraints of the head coil. As a result, STI has not yet been widely applied in human studies in vivo. In this work, we tackle these issues by proposing an image reconstruction algorithm for STI that leverages data-driven priors. Our method, called DeepSTI, learns the data prior implicitly via a deep neural network that approximates the proximal operator of a regularizer function for STI. The dipole inversion problem is then solved iteratively using the learned proximal network. Experimental results using both simulation and in vivo human data demonstrate great improvement over state-of-the-art algorithms in terms of the reconstructed tensor image, principal eigenvector maps and tractography results, while allowing for tensor reconstruction with MR phase measured at much less than six different orientations. Notably, promising reconstruction results are achieved by our method from only one orientation in human in vivo, and we demonstrate a potential application of this technique for estimating lesion susceptibility anisotropy in patients with multiple sclerosis.

Learned Proximal Networks for Quantitative Susceptibility Mapping

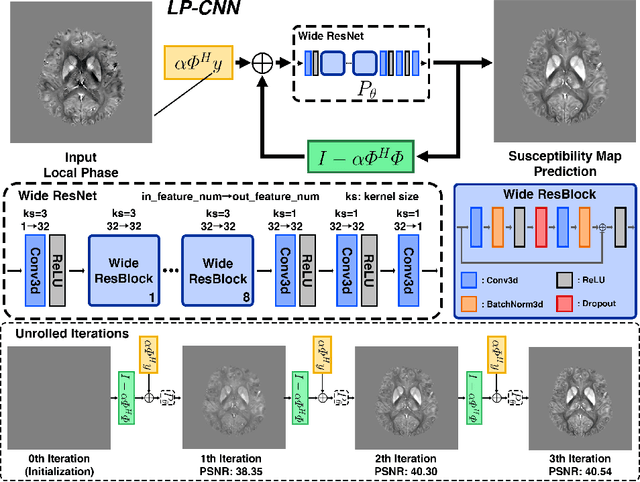
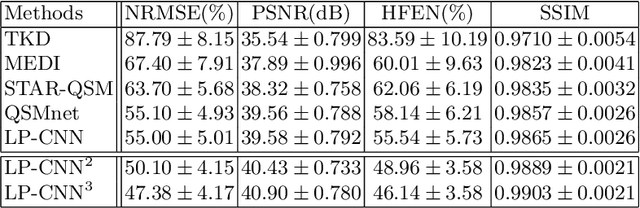
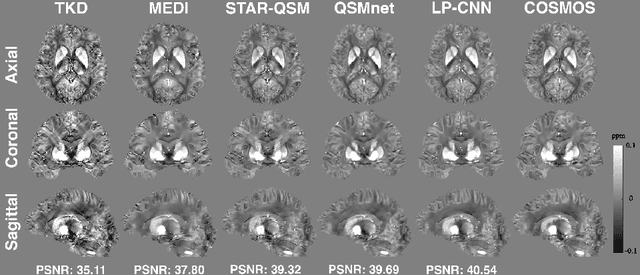
Quantitative Susceptibility Mapping (QSM) estimates tissue magnetic susceptibility distributions from Magnetic Resonance (MR) phase measurements by solving an ill-posed dipole inversion problem. Conventional single orientation QSM methods usually employ regularization strategies to stabilize such inversion, but may suffer from streaking artifacts or over-smoothing. Multiple orientation QSM such as calculation of susceptibility through multiple orientation sampling (COSMOS) can give well-conditioned inversion and an artifact free solution but has expensive acquisition costs. On the other hand, Convolutional Neural Networks (CNN) show great potential for medical image reconstruction, albeit often with limited interpretability. Here, we present a Learned Proximal Convolutional Neural Network (LP-CNN) for solving the ill-posed QSM dipole inversion problem in an iterative proximal gradient descent fashion. This approach combines the strengths of data-driven restoration priors and the clear interpretability of iterative solvers that can take into account the physical model of dipole convolution. During training, our LP-CNN learns an implicit regularizer via its proximal, enabling the decoupling between the forward operator and the data-driven parameters in the reconstruction algorithm. More importantly, this framework is believed to be the first deep learning QSM approach that can naturally handle an arbitrary number of phase input measurements without the need for any ad-hoc rotation or re-training. We demonstrate that the LP-CNN provides state-of-the-art reconstruction results compared to both traditional and deep learning methods while allowing for more flexibility in the reconstruction process.