Masked Completion via Structured Diffusion with White-Box Transformers

Modern learning frameworks often train deep neural networks with massive amounts of unlabeled data to learn representations by solving simple pretext tasks, then use the representations as foundations for downstream tasks. These networks are empirically designed; as such, they are usually not interpretable, their representations are not structured, and their designs are potentially redundant. White-box deep networks, in which each layer explicitly identifies and transforms structures in the data, present a promising alternative. However, existing white-box architectures have only been shown to work at scale in supervised settings with labeled data, such as classification. In this work, we provide the first instantiation of the white-box design paradigm that can be applied to large-scale unsupervised representation learning. We do this by exploiting a fundamental connection between diffusion, compression, and (masked) completion, deriving a deep transformer-like masked autoencoder architecture, called CRATE-MAE, in which the role of each layer is mathematically fully interpretable: they transform the data distribution to and from a structured representation. Extensive empirical evaluations confirm our analytical insights. CRATE-MAE demonstrates highly promising performance on large-scale imagery datasets while using only ~30% of the parameters compared to the standard masked autoencoder with the same model configuration. The representations learned by CRATE-MAE have explicit structure and also contain semantic meaning. Code is available at https://github.com/Ma-Lab-Berkeley/CRATE .

White-Box Transformers via Sparse Rate Reduction: Compression Is All There Is?

In this paper, we contend that a natural objective of representation learning is to compress and transform the distribution of the data, say sets of tokens, towards a low-dimensional Gaussian mixture supported on incoherent subspaces. The goodness of such a representation can be evaluated by a principled measure, called sparse rate reduction, that simultaneously maximizes the intrinsic information gain and extrinsic sparsity of the learned representation. From this perspective, popular deep network architectures, including transformers, can be viewed as realizing iterative schemes to optimize this measure. Particularly, we derive a transformer block from alternating optimization on parts of this objective: the multi-head self-attention operator compresses the representation by implementing an approximate gradient descent step on the coding rate of the features, and the subsequent multi-layer perceptron sparsifies the features. This leads to a family of white-box transformer-like deep network architectures, named CRATE, which are mathematically fully interpretable. We show, by way of a novel connection between denoising and compression, that the inverse to the aforementioned compressive encoding can be realized by the same class of CRATE architectures. Thus, the so-derived white-box architectures are universal to both encoders and decoders. Experiments show that these networks, despite their simplicity, indeed learn to compress and sparsify representations of large-scale real-world image and text datasets, and achieve performance very close to highly engineered transformer-based models: ViT, MAE, DINO, BERT, and GPT2. We believe the proposed computational framework demonstrates great potential in bridging the gap between theory and practice of deep learning, from a unified perspective of data compression. Code is available at: https://ma-lab-berkeley.github.io/CRATE .

What's in a Prior? Learned Proximal Networks for Inverse Problems

Proximal operators are ubiquitous in inverse problems, commonly appearing as part of algorithmic strategies to regularize problems that are otherwise ill-posed. Modern deep learning models have been brought to bear for these tasks too, as in the framework of plug-and-play or deep unrolling, where they loosely resemble proximal operators. Yet, something essential is lost in employing these purely data-driven approaches: there is no guarantee that a general deep network represents the proximal operator of any function, nor is there any characterization of the function for which the network might provide some approximate proximal. This not only makes guaranteeing convergence of iterative schemes challenging but, more fundamentally, complicates the analysis of what has been learned by these networks about their training data. Herein we provide a framework to develop learned proximal networks (LPN), prove that they provide exact proximal operators for a data-driven nonconvex regularizer, and show how a new training strategy, dubbed proximal matching, provably promotes the recovery of the log-prior of the true data distribution. Such LPN provide general, unsupervised, expressive proximal operators that can be used for general inverse problems with convergence guarantees. We illustrate our results in a series of cases of increasing complexity, demonstrating that these models not only result in state-of-the-art performance, but provide a window into the resulting priors learned from data.

Emergence of Segmentation with Minimalistic White-Box Transformers

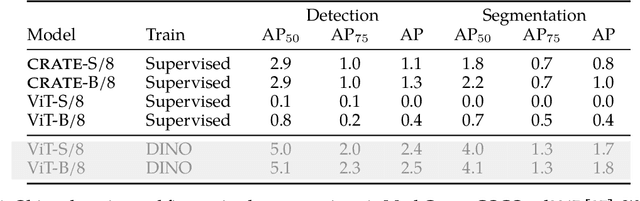
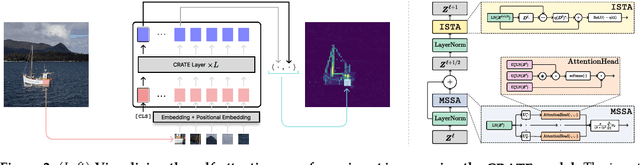
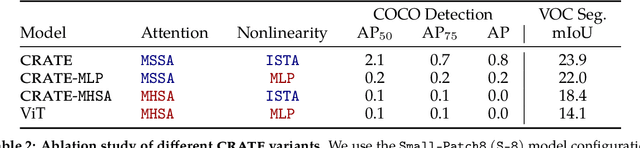
Transformer-like models for vision tasks have recently proven effective for a wide range of downstream applications such as segmentation and detection. Previous works have shown that segmentation properties emerge in vision transformers (ViTs) trained using self-supervised methods such as DINO, but not in those trained on supervised classification tasks. In this study, we probe whether segmentation emerges in transformer-based models solely as a result of intricate self-supervised learning mechanisms, or if the same emergence can be achieved under much broader conditions through proper design of the model architecture. Through extensive experimental results, we demonstrate that when employing a white-box transformer-like architecture known as CRATE, whose design explicitly models and pursues low-dimensional structures in the data distribution, segmentation properties, at both the whole and parts levels, already emerge with a minimalistic supervised training recipe. Layer-wise finer-grained analysis reveals that the emergent properties strongly corroborate the designed mathematical functions of the white-box network. Our results suggest a path to design white-box foundation models that are simultaneously highly performant and mathematically fully interpretable. Code is at \url{https://github.com/Ma-Lab-Berkeley/CRATE}.

Canonical Factors for Hybrid Neural Fields

Factored feature volumes offer a simple way to build more compact, efficient, and intepretable neural fields, but also introduce biases that are not necessarily beneficial for real-world data. In this work, we (1) characterize the undesirable biases that these architectures have for axis-aligned signals -- they can lead to radiance field reconstruction differences of as high as 2 PSNR -- and (2) explore how learning a set of canonicalizing transformations can improve representations by removing these biases. We prove in a two-dimensional model problem that simultaneously learning these transformations together with scene appearance succeeds with drastically improved efficiency. We validate the resulting architectures, which we call TILTED, using image, signed distance, and radiance field reconstruction tasks, where we observe improvements across quality, robustness, compactness, and runtime. Results demonstrate that TILTED can enable capabilities comparable to baselines that are 2x larger, while highlighting weaknesses of neural field evaluation procedures.

White-Box Transformers via Sparse Rate Reduction

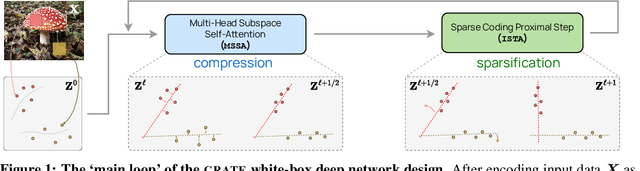
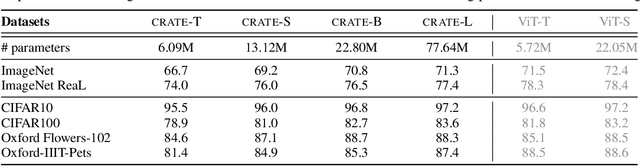
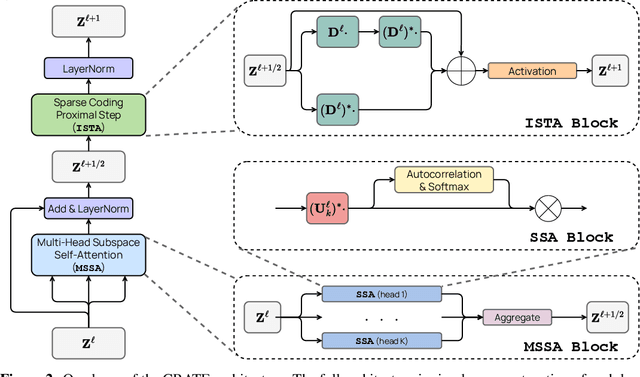
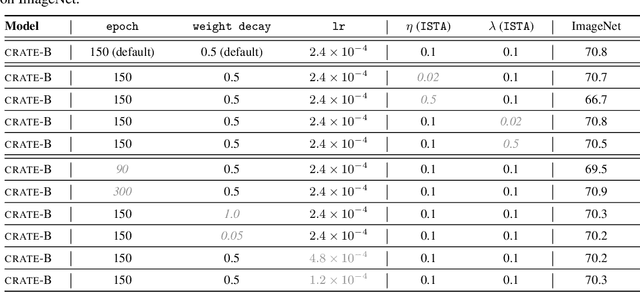
In this paper, we contend that the objective of representation learning is to compress and transform the distribution of the data, say sets of tokens, towards a mixture of low-dimensional Gaussian distributions supported on incoherent subspaces. The quality of the final representation can be measured by a unified objective function called sparse rate reduction. From this perspective, popular deep networks such as transformers can be naturally viewed as realizing iterative schemes to optimize this objective incrementally. Particularly, we show that the standard transformer block can be derived from alternating optimization on complementary parts of this objective: the multi-head self-attention operator can be viewed as a gradient descent step to compress the token sets by minimizing their lossy coding rate, and the subsequent multi-layer perceptron can be viewed as attempting to sparsify the representation of the tokens. This leads to a family of white-box transformer-like deep network architectures which are mathematically fully interpretable. Despite their simplicity, experiments show that these networks indeed learn to optimize the designed objective: they compress and sparsify representations of large-scale real-world vision datasets such as ImageNet, and achieve performance very close to thoroughly engineered transformers such as ViT. Code is at \url{https://github.com/Ma-Lab-Berkeley/CRATE}.

Resource-Efficient Invariant Networks: Exponential Gains by Unrolled Optimization

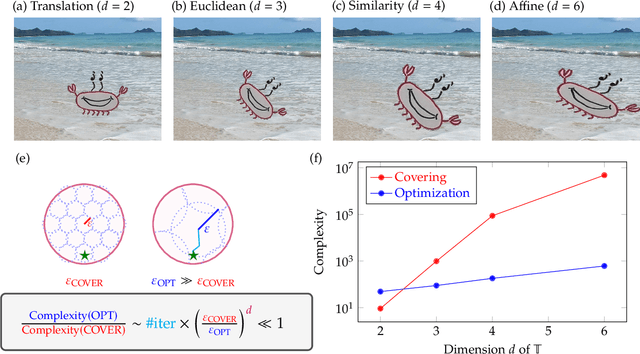
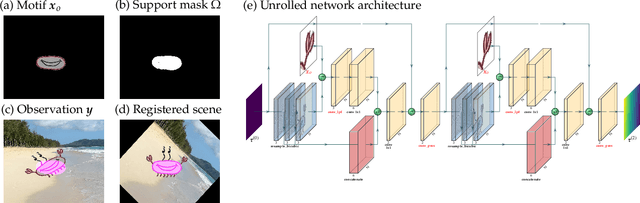
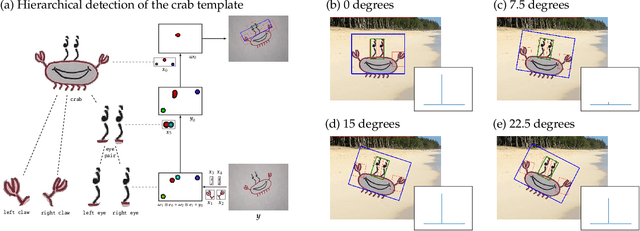
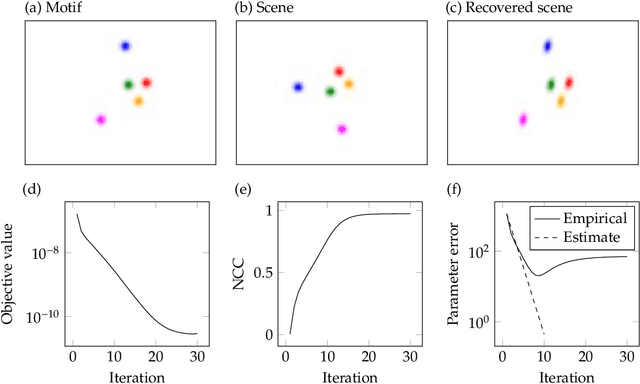
Achieving invariance to nuisance transformations is a fundamental challenge in the construction of robust and reliable vision systems. Existing approaches to invariance scale exponentially with the dimension of the family of transformations, making them unable to cope with natural variabilities in visual data such as changes in pose and perspective. We identify a common limitation of these approaches--they rely on sampling to traverse the high-dimensional space of transformations--and propose a new computational primitive for building invariant networks based instead on optimization, which in many scenarios provides a provably more efficient method for high-dimensional exploration than sampling. We provide empirical and theoretical corroboration of the efficiency gains and soundness of our proposed method, and demonstrate its utility in constructing an efficient invariant network for a simple hierarchical object detection task when combined with unrolled optimization. Code for our networks and experiments is available at https://github.com/sdbuch/refine.

Deep Networks Provably Classify Data on Curves

Data with low-dimensional nonlinear structure are ubiquitous in engineering and scientific problems. We study a model problem with such structure -- a binary classification task that uses a deep fully-connected neural network to classify data drawn from two disjoint smooth curves on the unit sphere. Aside from mild regularity conditions, we place no restrictions on the configuration of the curves. We prove that when (i) the network depth is large relative to certain geometric properties that set the difficulty of the problem and (ii) the network width and number of samples is polynomial in the depth, randomly-initialized gradient descent quickly learns to correctly classify all points on the two curves with high probability. To our knowledge, this is the first generalization guarantee for deep networks with nonlinear data that depends only on intrinsic data properties. Our analysis proceeds by a reduction to dynamics in the neural tangent kernel (NTK) regime, where the network depth plays the role of a fitting resource in solving the classification problem. In particular, via fine-grained control of the decay properties of the NTK, we demonstrate that when the network is sufficiently deep, the NTK can be locally approximated by a translationally invariant operator on the manifolds and stably inverted over smooth functions, which guarantees convergence and generalization.

Deep Networks and the Multiple Manifold Problem

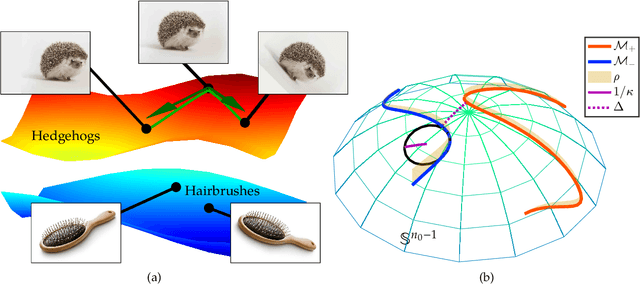
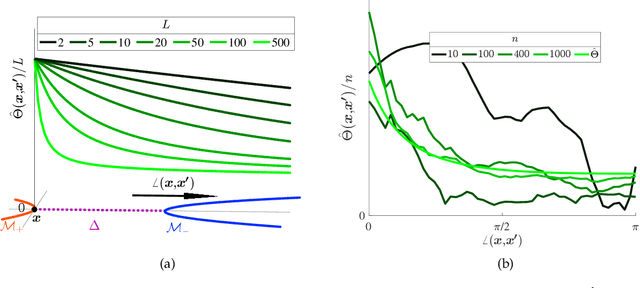
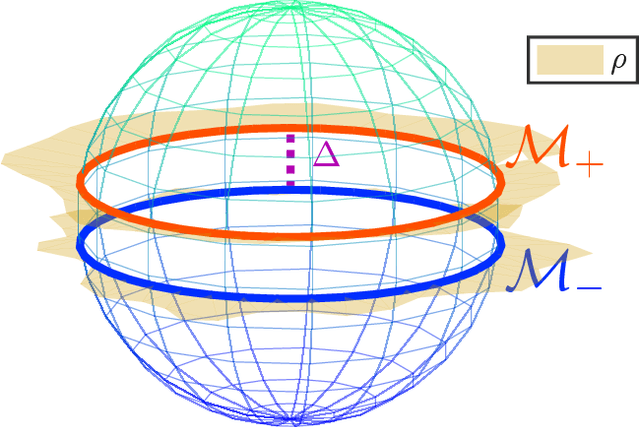
We study the multiple manifold problem, a binary classification task modeled on applications in machine vision, in which a deep fully-connected neural network is trained to separate two low-dimensional submanifolds of the unit sphere. We provide an analysis of the one-dimensional case, proving for a simple manifold configuration that when the network depth $L$ is large relative to certain geometric and statistical properties of the data, the network width $n$ grows as a sufficiently large polynomial in $L$, and the number of i.i.d. samples from the manifolds is polynomial in $L$, randomly-initialized gradient descent rapidly learns to classify the two manifolds perfectly with high probability. Our analysis demonstrates concrete benefits of depth and width in the context of a practically-motivated model problem: the depth acts as a fitting resource, with larger depths corresponding to smoother networks that can more readily separate the class manifolds, and the width acts as a statistical resource, enabling concentration of the randomly-initialized network and its gradients. The argument centers around the neural tangent kernel and its role in the nonasymptotic analysis of training overparameterized neural networks; to this literature, we contribute essentially optimal rates of concentration for the neural tangent kernel of deep fully-connected networks, requiring width $n \gtrsim L\,\mathrm{poly}(d_0)$ to achieve uniform concentration of the initial kernel over a $d_0$-dimensional submanifold of the unit sphere $\mathbb{S}^{n_0-1}$, and a nonasymptotic framework for establishing generalization of networks trained in the NTK regime with structured data. The proof makes heavy use of martingale concentration to optimally treat statistical dependencies across layers of the initial random network. This approach should be of use in establishing similar results for other network architectures.