Sequencing the Neurome: Towards Scalable Exact Parameter Reconstruction of Black-Box Neural Networks

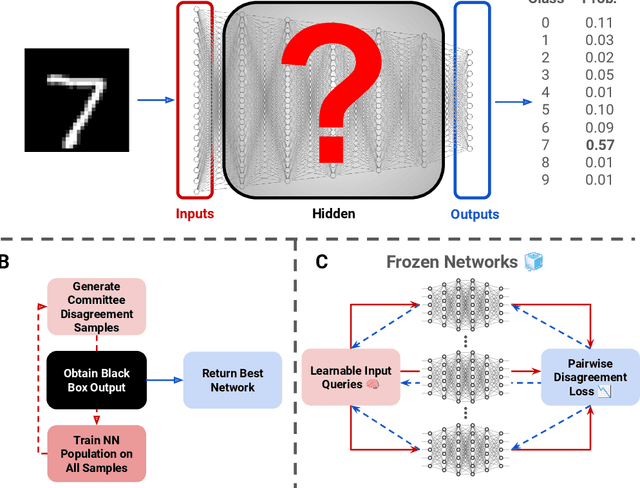
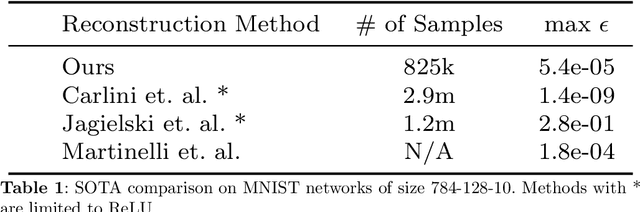
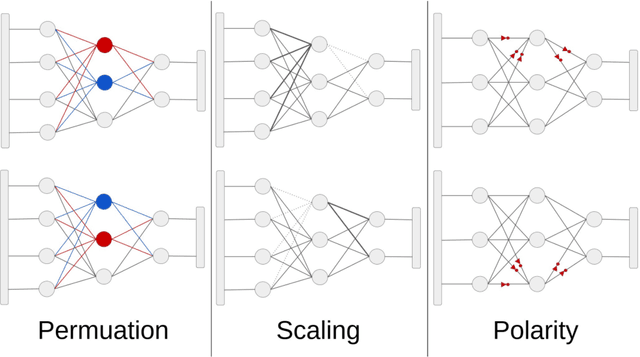
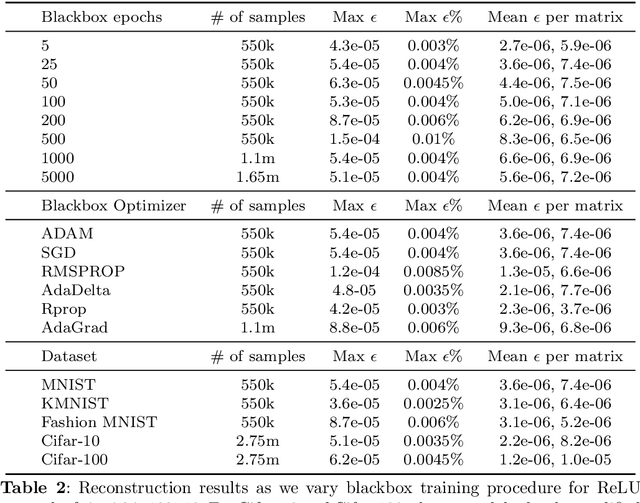
Inferring the exact parameters of a neural network with only query access is an NP-Hard problem, with few practical existing algorithms. Solutions would have major implications for security, verification, interpretability, and understanding biological networks. The key challenges are the massive parameter space, and complex non-linear relationships between neurons. We resolve these challenges using two insights. First, we observe that almost all networks used in practice are produced by random initialization and first order optimization, an inductive bias that drastically reduces the practical parameter space. Second, we present a novel query generation algorithm that produces maximally informative samples, letting us untangle the non-linear relationships efficiently. We demonstrate reconstruction of a hidden network containing over 1.5 million parameters, and of one 7 layers deep, the largest and deepest reconstructions to date, with max parameter difference less than 0.0001, and illustrate robustness and scalability across a variety of architectures, datasets, and training procedures.

TpopT: Efficient Trainable Template Optimization on Low-Dimensional Manifolds

In scientific and engineering scenarios, a recurring task is the detection of low-dimensional families of signals or patterns. A classic family of approaches, exemplified by template matching, aims to cover the search space with a dense template bank. While simple and highly interpretable, it suffers from poor computational efficiency due to unfavorable scaling in the signal space dimensionality. In this work, we study TpopT (TemPlate OPTimization) as an alternative scalable framework for detecting low-dimensional families of signals which maintains high interpretability. We provide a theoretical analysis of the convergence of Riemannian gradient descent for TpopT, and prove that it has a superior dimension scaling to covering. We also propose a practical TpopT framework for nonparametric signal sets, which incorporates techniques of embedding and kernel interpolation, and is further configurable into a trainable network architecture by unrolled optimization. The proposed trainable TpopT exhibits significantly improved efficiency-accuracy tradeoffs for gravitational wave detection, where matched filtering is currently a method of choice. We further illustrate the general applicability of this approach with experiments on handwritten digit data.

Boosting the Efficiency of Parametric Detection with Hierarchical Neural Networks

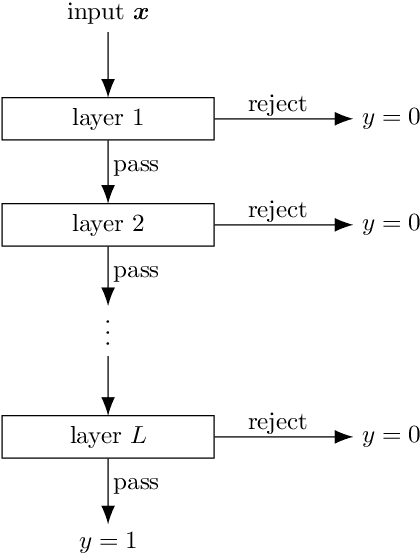
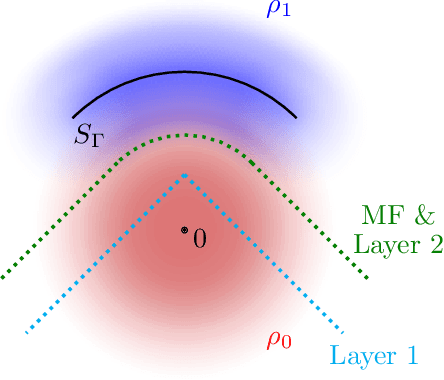
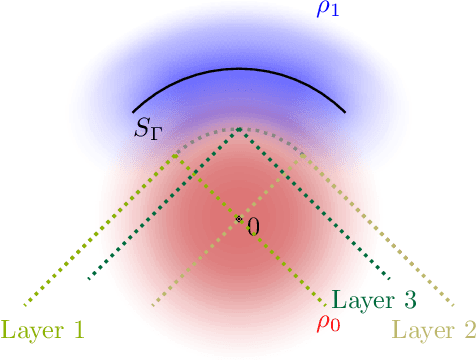
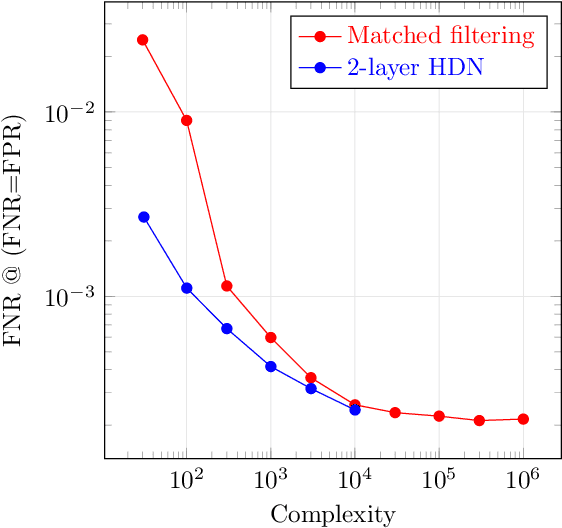
Gravitational wave astronomy is a vibrant field that leverages both classic and modern data processing techniques for the understanding of the universe. Various approaches have been proposed for improving the efficiency of the detection scheme, with hierarchical matched filtering being an important strategy. Meanwhile, deep learning methods have recently demonstrated both consistency with matched filtering methods and remarkable statistical performance. In this work, we propose Hierarchical Detection Network (HDN), a novel approach to efficient detection that combines ideas from hierarchical matching and deep learning. The network is trained using a novel loss function, which encodes simultaneously the goals of statistical accuracy and efficiency. We discuss the source of complexity reduction of the proposed model, and describe a general recipe for initialization with each layer specializing in different regions. We demonstrate the performance of HDN with experiments using open LIGO data and synthetic injections, and observe with two-layer models a $79\%$ efficiency gain compared with matched filtering at an equal error rate of $0.2\%$. Furthermore, we show how training a three-layer HDN initialized using two-layer model can further boost both accuracy and efficiency, highlighting the power of multiple simple layers in efficient detection.

Resource-Efficient Invariant Networks: Exponential Gains by Unrolled Optimization

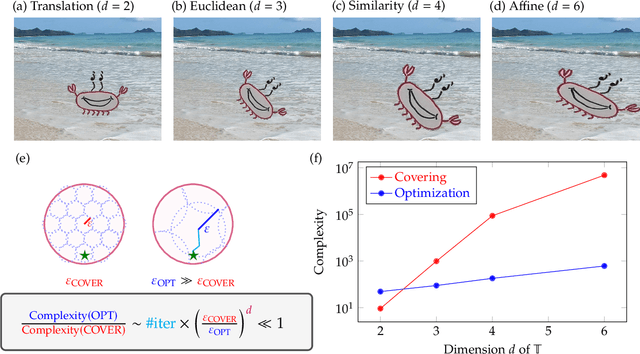
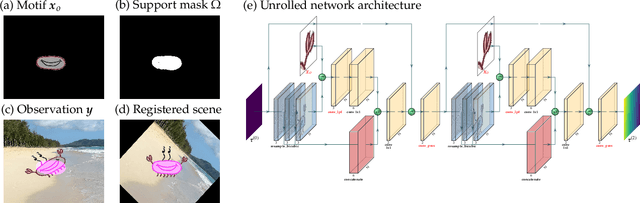
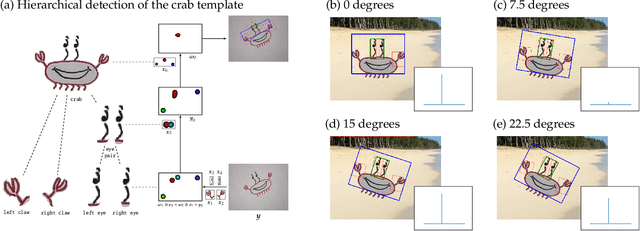
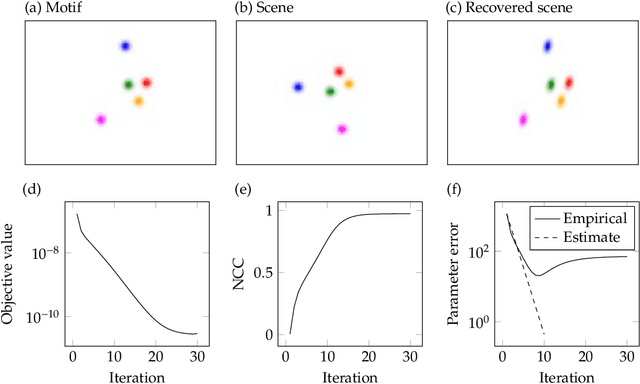
Achieving invariance to nuisance transformations is a fundamental challenge in the construction of robust and reliable vision systems. Existing approaches to invariance scale exponentially with the dimension of the family of transformations, making them unable to cope with natural variabilities in visual data such as changes in pose and perspective. We identify a common limitation of these approaches--they rely on sampling to traverse the high-dimensional space of transformations--and propose a new computational primitive for building invariant networks based instead on optimization, which in many scenarios provides a provably more efficient method for high-dimensional exploration than sampling. We provide empirical and theoretical corroboration of the efficiency gains and soundness of our proposed method, and demonstrate its utility in constructing an efficient invariant network for a simple hierarchical object detection task when combined with unrolled optimization. Code for our networks and experiments is available at https://github.com/sdbuch/refine.

Principal Component Pursuit for Pattern Identification in Environmental Mixtures

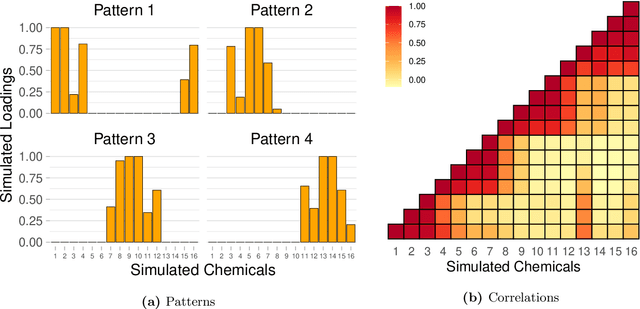
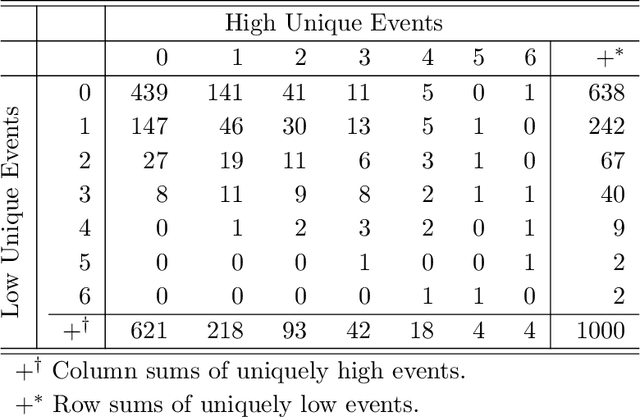
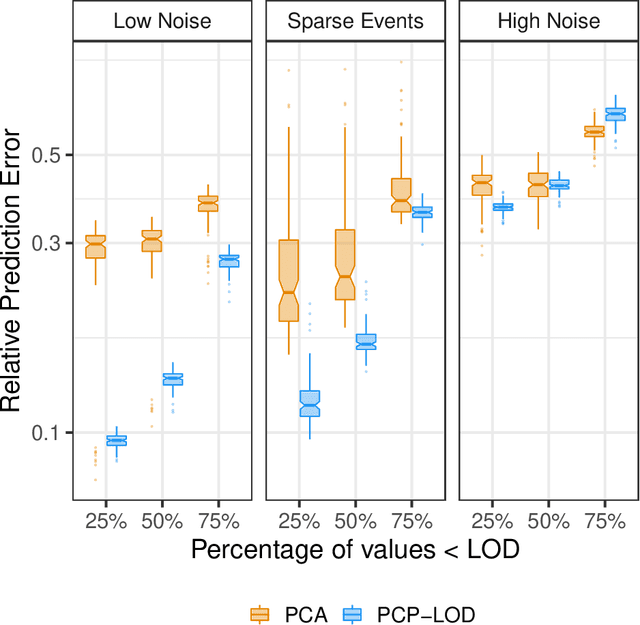
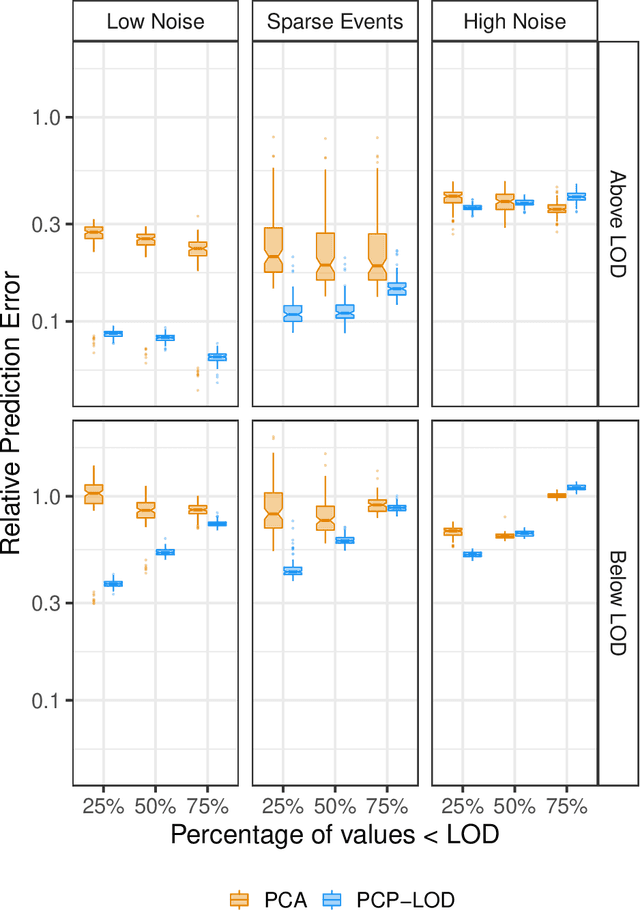
Environmental health researchers often aim to identify sources/behaviors that give rise to potentially harmful exposures. We adapted principal component pursuit (PCP)-a robust technique for dimensionality reduction in computer vision and signal processing-to identify patterns in environmental mixtures. PCP decomposes the exposure mixture into a low-rank matrix containing consistent exposure patterns across pollutants and a sparse matrix isolating unique exposure events. We adapted PCP to accommodate non-negative and missing data, and values below a given limit of detection (LOD). We simulated data to represent environmental mixtures of two sizes with increasing proportions <LOD and three noise structures. We compared PCP-LOD to principal component analysis (PCA) to evaluate performance. We next applied PCP-LOD to a mixture of 21 persistent organic pollutants (POPs) measured in 1,000 U.S. adults from the 2001-2002 National Health and Nutrition Examination Survey. We applied singular value decomposition to the estimated low-rank matrix to characterize the patterns. PCP-LOD recovered the true number of patterns through cross-validation for all simulations; based on an a priori specified criterion, PCA recovered the true number of patterns in 32% of simulations. PCP-LOD achieved lower relative predictive error than PCA for all simulated datasets with up to 50% of the data <LOD. When 75% of values were <LOD, PCP-LOD outperformed PCA only when noise was low. In the POP mixture, PCP-LOD identified a rank-three underlying structure and separated 6% of values as unique events. One pattern represented comprehensive exposure to all POPs. The other patterns grouped chemicals based on known structure and toxicity. PCP-LOD serves as a useful tool to express multi-dimensional exposures as consistent patterns that, if found to be related to adverse health, are amenable to targeted interventions.

Deep Networks Provably Classify Data on Curves

Data with low-dimensional nonlinear structure are ubiquitous in engineering and scientific problems. We study a model problem with such structure -- a binary classification task that uses a deep fully-connected neural network to classify data drawn from two disjoint smooth curves on the unit sphere. Aside from mild regularity conditions, we place no restrictions on the configuration of the curves. We prove that when (i) the network depth is large relative to certain geometric properties that set the difficulty of the problem and (ii) the network width and number of samples is polynomial in the depth, randomly-initialized gradient descent quickly learns to correctly classify all points on the two curves with high probability. To our knowledge, this is the first generalization guarantee for deep networks with nonlinear data that depends only on intrinsic data properties. Our analysis proceeds by a reduction to dynamics in the neural tangent kernel (NTK) regime, where the network depth plays the role of a fitting resource in solving the classification problem. In particular, via fine-grained control of the decay properties of the NTK, we demonstrate that when the network is sufficiently deep, the NTK can be locally approximated by a translationally invariant operator on the manifolds and stably inverted over smooth functions, which guarantees convergence and generalization.

Square Root Principal Component Pursuit: Tuning-Free Noisy Robust Matrix Recovery

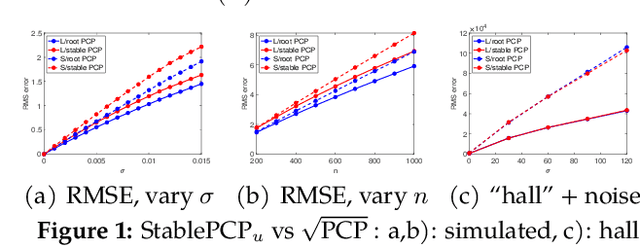
We propose a new framework -- Square Root Principal Component Pursuit -- for low-rank matrix recovery from observations corrupted with noise and outliers. Inspired by the square root Lasso, this new formulation does not require prior knowledge of the noise level. We show that a single, universal choice of the regularization parameter suffices to achieve reconstruction error proportional to the (a priori unknown) noise level. In comparison, previous formulations such as stable PCP rely on noise-dependent parameters to achieve similar performance, and are therefore challenging to deploy in applications where the noise level is unknown. We validate the effectiveness of our new method through experiments on simulated and real datasets. Our simulations corroborate the claim that a universal choice of the regularization parameter yields near optimal performance across a range of noise levels, indicating that the proposed method outperforms the (somewhat loose) bound proved here.

ReduNet: A White-box Deep Network from the Principle of Maximizing Rate Reduction

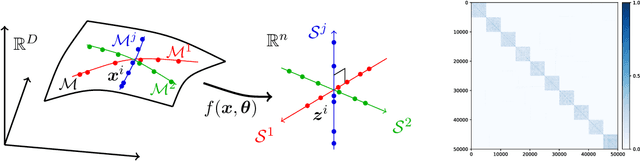
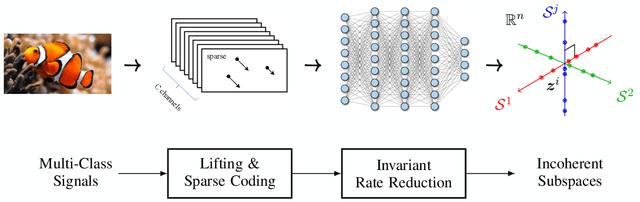
This work attempts to provide a plausible theoretical framework that aims to interpret modern deep (convolutional) networks from the principles of data compression and discriminative representation. We argue that for high-dimensional multi-class data, the optimal linear discriminative representation maximizes the coding rate difference between the whole dataset and the average of all the subsets. We show that the basic iterative gradient ascent scheme for optimizing the rate reduction objective naturally leads to a multi-layer deep network, named ReduNet, which shares common characteristics of modern deep networks. The deep layered architectures, linear and nonlinear operators, and even parameters of the network are all explicitly constructed layer-by-layer via forward propagation, although they are amenable to fine-tuning via back propagation. All components of so-obtained ``white-box'' network have precise optimization, statistical, and geometric interpretation. Moreover, all linear operators of the so-derived network naturally become multi-channel convolutions when we enforce classification to be rigorously shift-invariant. The derivation in the invariant setting suggests a trade-off between sparsity and invariance, and also indicates that such a deep convolution network is significantly more efficient to construct and learn in the spectral domain. Our preliminary simulations and experiments clearly verify the effectiveness of both the rate reduction objective and the associated ReduNet. All code and data are available at https://github.com/Ma-Lab-Berkeley.

Generalized Approach to Matched Filtering using Neural Networks

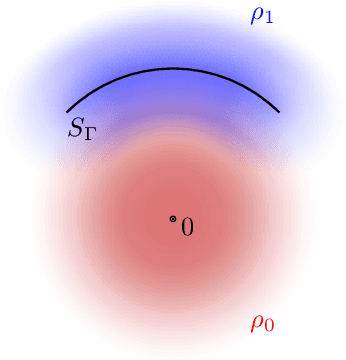
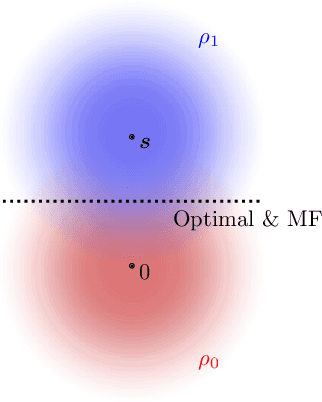
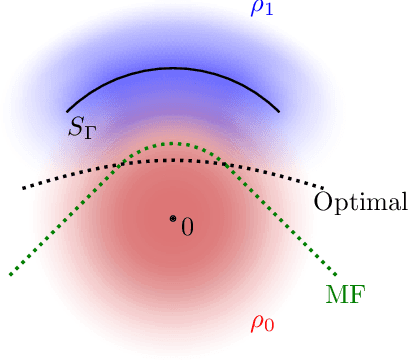
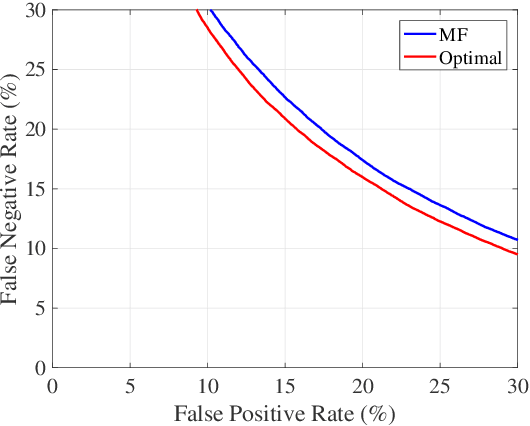
Gravitational wave science is a pioneering field with rapidly evolving data analysis methodology currently assimilating and inventing deep learning techniques. The bulk of the sophisticated flagship searches of the field rely on the time-tested matched filtering principle within their core. In this paper, we make a key observation on the relationship between the emerging deep learning and the traditional techniques: matched filtering is formally equivalent to a particular neural network. This means that a neural network can be constructed analytically to exactly implement matched filtering, and can be further trained on data or boosted with additional complexity for improved performance. This fundamental equivalence allows us to define a "complexity standard candle" allowing us to characterize the relative complexity of the different approaches to gravitational wave signals in a common framework. Additionally it also provides a glimpse of an intriguing symmetry that could provide clues on how neural networks approach the problem of finding signals in overwhelming noise. Moreover, we show that the proposed neural network architecture can outperform matched filtering, both with or without knowledge of a prior on the parameter distribution. When a prior is given, the proposed neural network can approach the statistically optimal performance. We also propose and investigate two different neural network architectures MNet-Shallow and MNet-Deep, both of which implement matched filtering at initialization and can be trained on data. MNet-Shallow has simpler structure, while MNet-Deep is more flexible and can deal with a wider range of distributions. Our theoretical findings are corroborated by experiments using real LIGO data and synthetic injections. Finally, our results suggest new perspectives on the role of deep learning in gravitational wave detection.

Deep Networks from the Principle of Rate Reduction

This work attempts to interpret modern deep (convolutional) networks from the principles of rate reduction and (shift) invariant classification. We show that the basic iterative gradient ascent scheme for optimizing the rate reduction of learned features naturally leads to a multi-layer deep network, one iteration per layer. The layered architectures, linear and nonlinear operators, and even parameters of the network are all explicitly constructed layer-by-layer in a forward propagation fashion by emulating the gradient scheme. All components of this "white box" network have precise optimization, statistical, and geometric interpretation. This principled framework also reveals and justifies the role of multi-channel lifting and sparse coding in early stage of deep networks. Moreover, all linear operators of the so-derived network naturally become multi-channel convolutions when we enforce classification to be rigorously shift-invariant. The derivation also indicates that such a convolutional network is significantly more efficient to construct and learn in the spectral domain. Our preliminary simulations and experiments indicate that so constructed deep network can already learn a good discriminative representation even without any back propagation training.