Sequencing the Neurome: Towards Scalable Exact Parameter Reconstruction of Black-Box Neural Networks

Inferring the exact parameters of a neural network with only query access is an NP-Hard problem, with few practical existing algorithms. Solutions would have major implications for security, verification, interpretability, and understanding biological networks. The key challenges are the massive parameter space, and complex non-linear relationships between neurons. We resolve these challenges using two insights. First, we observe that almost all networks used in practice are produced by random initialization and first order optimization, an inductive bias that drastically reduces the practical parameter space. Second, we present a novel query generation algorithm that produces maximally informative samples, letting us untangle the non-linear relationships efficiently. We demonstrate reconstruction of a hidden network containing over 1.5 million parameters, and of one 7 layers deep, the largest and deepest reconstructions to date, with max parameter difference less than 0.0001, and illustrate robustness and scalability across a variety of architectures, datasets, and training procedures.

Diffusion Models Are Promising for Ab Initio Structure Solutions from Nanocrystalline Powder Diffraction Data

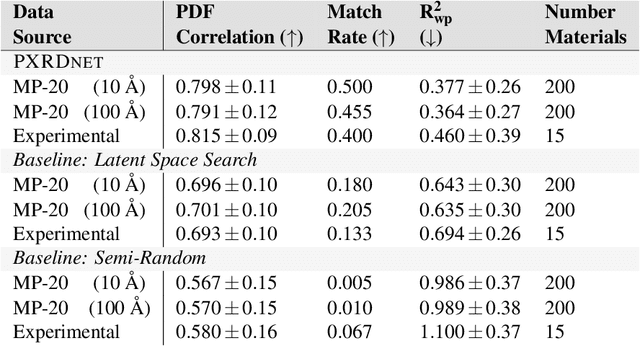
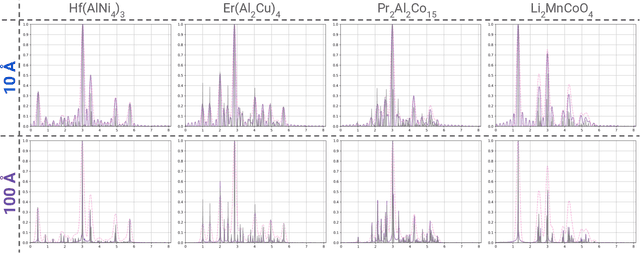
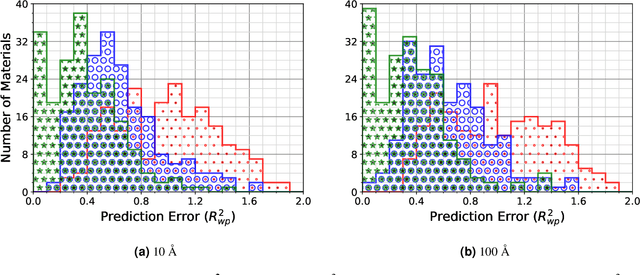
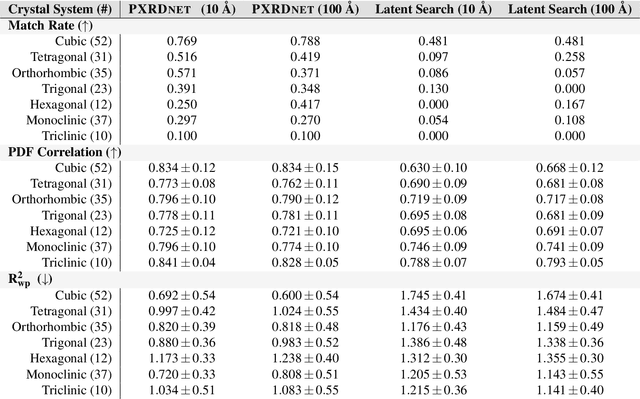
A major challenge in materials science is the determination of the structure of nanometer sized objects. Here we present a novel approach that uses a generative machine learning model based on a Diffusion model that is trained on 45,229 known structures. The model factors both the measured diffraction pattern as well as relevant statistical priors on the unit cell of atomic cluster structures. Conditioned only on the chemical formula and the information-scarce finite-size broadened powder diffraction pattern, we find that our model, PXRDnet, can successfully solve simulated nanocrystals as small as 10 angstroms across 200 materials of varying symmetry and complexity, including structures from all seven crystal systems. We show that our model can determine structural solutions with up to $81.5\%$ accuracy, as measured by structural correlation. Furthermore, PXRDnet is capable of solving structures from noisy diffraction patterns gathered in real-world experiments. We suggest that data driven approaches, bootstrapped from theoretical simulation, will ultimately provide a path towards determining the structure of previously unsolved nano-materials.

Towards End-to-End Structure Solutions from Information-Compromised Diffraction Data via Generative Deep Learning

The revolution in materials in the past century was built on a knowledge of the atomic arrangements and the structure-property relationship. The sine qua non for obtaining quantitative structural information is single crystal crystallography. However, increasingly we need to solve structures in cases where the information content in our input signal is significantly degraded, for example, due to orientational averaging of grains, finite size effects due to nanostructure, and mixed signals due to sample heterogeneity. Understanding the structure property relationships in such situations is, if anything, more important and insightful, yet we do not have robust approaches for accomplishing it. In principle, machine learning (ML) and deep learning (DL) are promising approaches since they augment information in the degraded input signal with prior knowledge learned from large databases of already known structures. Here we present a novel ML approach, a variational query-based multi-branch deep neural network that has the promise to be a robust but general tool to address this problem end-to-end. We demonstrate the approach on computed powder x-ray diffraction (PXRD), along with partial chemical composition information, as input. We choose as a structural representation a modified electron density we call the Cartesian mapped electron density (CMED), that straightforwardly allows our ML model to learn material structures across different chemistries, symmetries and crystal systems. When evaluated on theoretically simulated data for the cubic and trigonal crystal systems, the system achieves up to $93.4\%$ average similarity with the ground truth on unseen materials, both with known and partially-known chemical composition information, showing great promise for successful structure solution even from degraded and incomplete input data.