Square Root Principal Component Pursuit: Tuning-Free Noisy Robust Matrix Recovery
Paper and Code
Jun 17, 2021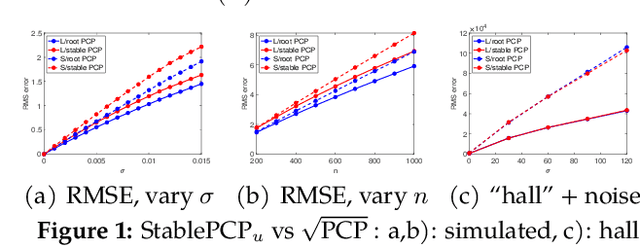



We propose a new framework -- Square Root Principal Component Pursuit -- for low-rank matrix recovery from observations corrupted with noise and outliers. Inspired by the square root Lasso, this new formulation does not require prior knowledge of the noise level. We show that a single, universal choice of the regularization parameter suffices to achieve reconstruction error proportional to the (a priori unknown) noise level. In comparison, previous formulations such as stable PCP rely on noise-dependent parameters to achieve similar performance, and are therefore challenging to deploy in applications where the noise level is unknown. We validate the effectiveness of our new method through experiments on simulated and real datasets. Our simulations corroborate the claim that a universal choice of the regularization parameter yields near optimal performance across a range of noise levels, indicating that the proposed method outperforms the (somewhat loose) bound proved here.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge