Principal Component Pursuit for Pattern Identification in Environmental Mixtures

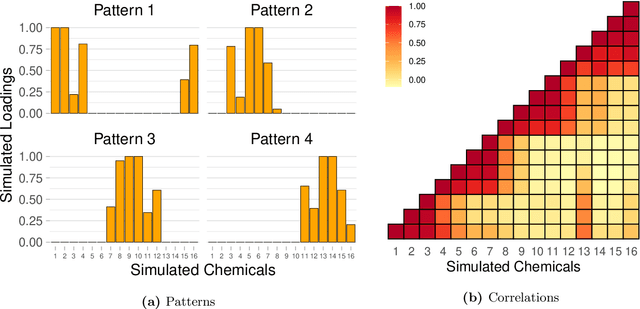
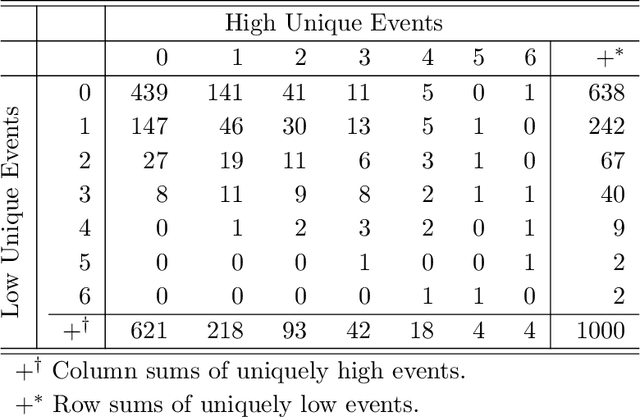
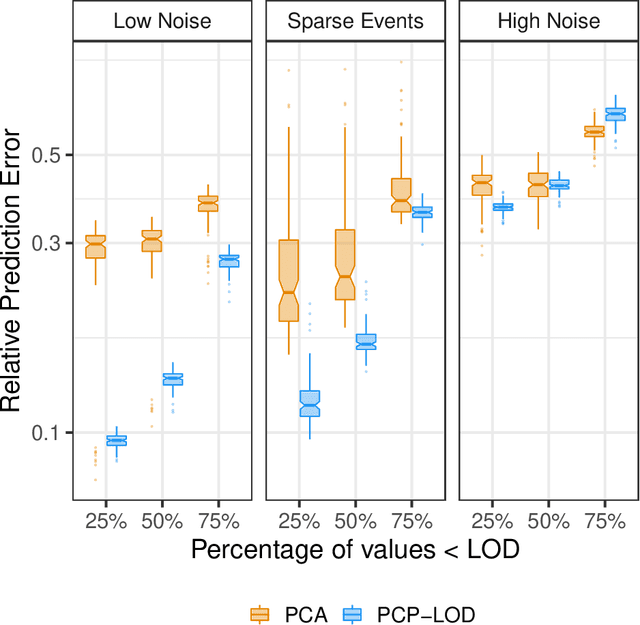
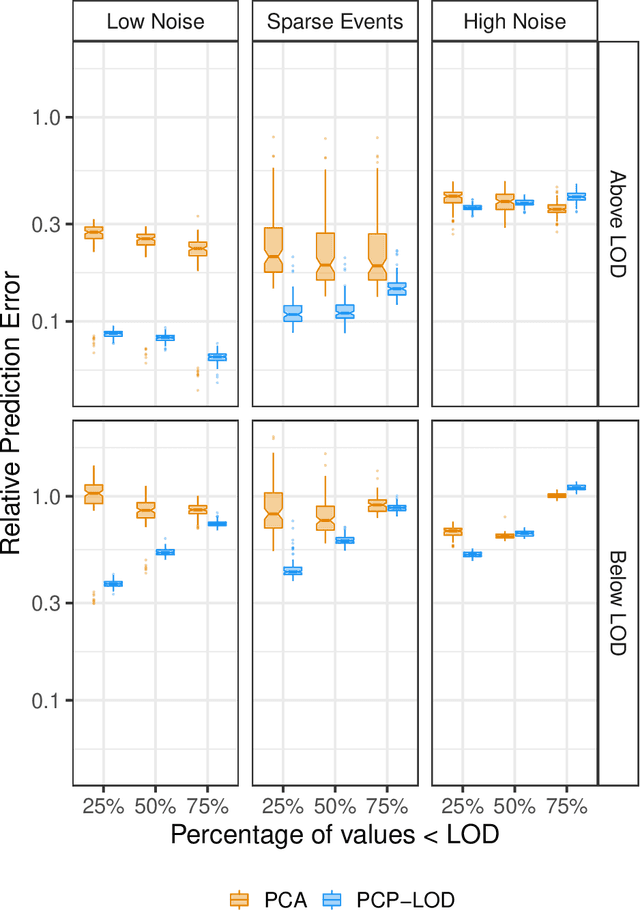
Environmental health researchers often aim to identify sources/behaviors that give rise to potentially harmful exposures. We adapted principal component pursuit (PCP)-a robust technique for dimensionality reduction in computer vision and signal processing-to identify patterns in environmental mixtures. PCP decomposes the exposure mixture into a low-rank matrix containing consistent exposure patterns across pollutants and a sparse matrix isolating unique exposure events. We adapted PCP to accommodate non-negative and missing data, and values below a given limit of detection (LOD). We simulated data to represent environmental mixtures of two sizes with increasing proportions <LOD and three noise structures. We compared PCP-LOD to principal component analysis (PCA) to evaluate performance. We next applied PCP-LOD to a mixture of 21 persistent organic pollutants (POPs) measured in 1,000 U.S. adults from the 2001-2002 National Health and Nutrition Examination Survey. We applied singular value decomposition to the estimated low-rank matrix to characterize the patterns. PCP-LOD recovered the true number of patterns through cross-validation for all simulations; based on an a priori specified criterion, PCA recovered the true number of patterns in 32% of simulations. PCP-LOD achieved lower relative predictive error than PCA for all simulated datasets with up to 50% of the data <LOD. When 75% of values were <LOD, PCP-LOD outperformed PCA only when noise was low. In the POP mixture, PCP-LOD identified a rank-three underlying structure and separated 6% of values as unique events. One pattern represented comprehensive exposure to all POPs. The other patterns grouped chemicals based on known structure and toxicity. PCP-LOD serves as a useful tool to express multi-dimensional exposures as consistent patterns that, if found to be related to adverse health, are amenable to targeted interventions.

Heterogeneous Distributed Lag Models to Estimate Personalized Effects of Maternal Exposures to Air Pollution

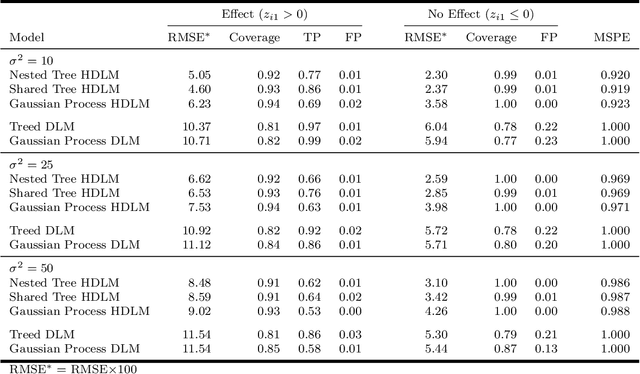
Children's health studies support an association between maternal environmental exposures and children's birth and health outcomes. A common goal in such studies is to identify critical windows of susceptibility -- periods during gestation with increased association between maternal exposures and a future outcome. The associations and timings of critical windows are likely heterogeneous across different levels of individual, family, and neighborhood characteristics. However, the few studies that have considered effect modification were limited to a few pre-specified subgroups. We propose a statistical learning method to estimate critical windows at the individual level and identify important characteristics that induce heterogeneity. The proposed approach uses distributed lag models (DLMs) modified by Bayesian additive regression trees to account for effect heterogeneity based on a potentially high-dimensional set of modifying factors. We show in a simulation study that our model can identify both critical windows and modifiers responsible for DLM heterogeneity. We estimate the relationship between weekly exposures to fine particulate matter during gestation and birth weight in an administrative Colorado birth cohort. We identify maternal body mass index (BMI), age, Hispanic designation, and education as modifiers of the distributed lag effects and find non-Hispanics with increased BMI to be a susceptible population.

Accurate Uncertainty Estimation and Decomposition in Ensemble Learning

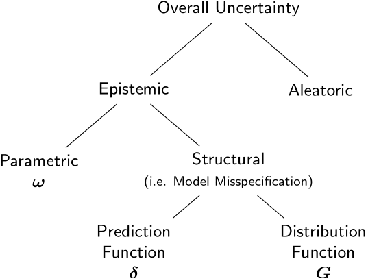
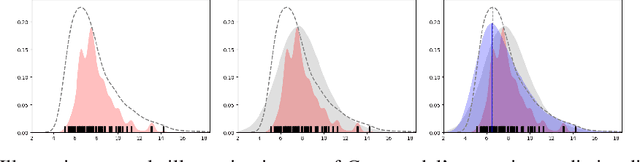
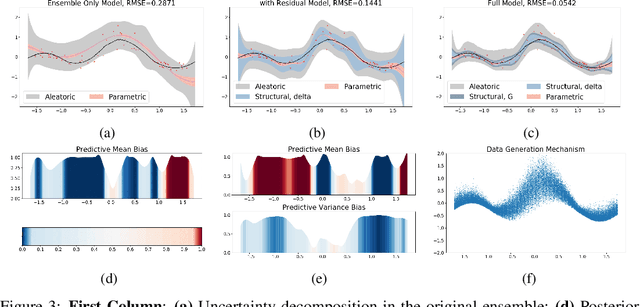
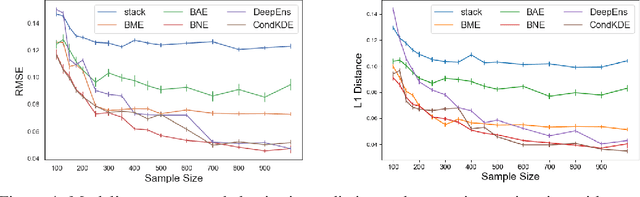
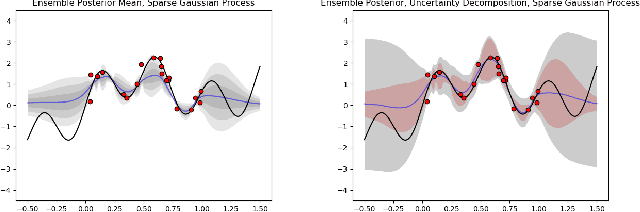
Ensemble learning is a standard approach to building machine learning systems that capture complex phenomena in real-world data. An important aspect of these systems is the complete and valid quantification of model uncertainty. We introduce a Bayesian nonparametric ensemble (BNE) approach that augments an existing ensemble model to account for different sources of model uncertainty. BNE augments a model's prediction and distribution functions using Bayesian nonparametric machinery. It has a theoretical guarantee in that it robustly estimates the uncertainty patterns in the data distribution, and can decompose its overall predictive uncertainty into distinct components that are due to different sources of noise and error. We show that our method achieves accurate uncertainty estimates under complex observational noise, and illustrate its real-world utility in terms of uncertainty decomposition and model bias detection for an ensemble in predict air pollution exposures in Eastern Massachusetts, USA.

Adaptive and Calibrated Ensemble Learning with Dependent Tail-free Process

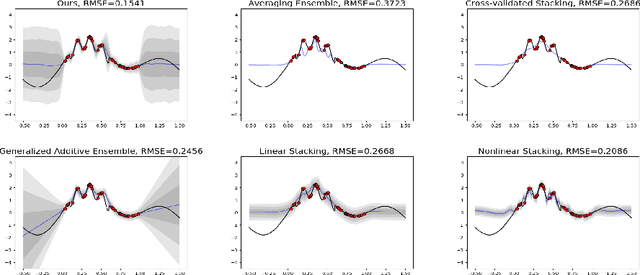
Ensemble learning is a mainstay in modern data science practice. Conventional ensemble algorithms assigns to base models a set of deterministic, constant model weights that (1) do not fully account for variations in base model accuracy across subgroups, nor (2) provide uncertainty estimates for the ensemble prediction, which could result in mis-calibrated (i.e. precise but biased) predictions that could in turn negatively impact the algorithm performance in real-word applications. In this work, we present an adaptive, probabilistic approach to ensemble learning using dependent tail-free process as ensemble weight prior. Given input feature $\mathbf{x}$, our method optimally combines base models based on their predictive accuracy in the feature space $\mathbf{x} \in \mathcal{X}$, and provides interpretable uncertainty estimates both in model selection and in ensemble prediction. To encourage scalable and calibrated inference, we derive a structured variational inference algorithm that jointly minimize KL objective and the model's calibration score (i.e. Continuous Ranked Probability Score (CRPS)). We illustrate the utility of our method on both a synthetic nonlinear function regression task, and on the real-world application of spatio-temporal integration of particle pollution prediction models in New England.